
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Проверка гипотезы о распределении с помощью критерия согласия ПирсонаСодержание книги
Поиск на нашем сайте
Ранее была выдвинута гипотеза о законе распределения рассматриваемой случайной величины. Сопоставление статистического распределения (гистограммы) и предполагаемого теоретического (графика плотности) показывает наличие некоторых расхождений между ними (см. рис.3). Объяснить возникновение несовпадений можно двумя разными способами: 1) Указанные расхождения несущественны и вызваны ограниченным количеством наблюдений и случайными факторами – случайностью результата единичного наблюдения, способа группировки данных и т. п. В этом случае выдвинутая гипотеза о распределении считается правдоподобной и принимается как не противоречащая опытным данным. 2) Указанные расхождения являются существенными (неслучайными) и связаны с тем, что действительное распределение случайной величины отличается от предполагаемого. В этом случае выдвинутая гипотеза о распределении отвергается как плохо согласующаяся с результатами наблюдений. Для выбора первого или второго варианта ответа служат так называемые критерии согласия. Существует несколько различных критериев согласия: К. Пирсона, А. Н. Колмогорова, Н. В. Смирнова и другие. Мы рассмотрим лишь критерий Пирсона, называемый также критерием c 2 («хи-квадрат»). Критерий Пирсона выгодно отличается от остальных, во-первых, применимостью к любым (дискретным, непрерывным) распределениям и, во-вторых, простотой вычислительного алгоритма. Группировка исходных данных Критерий Пирсона применяется к сгруппированным данным. Предположим, что было произведено n независимых опытов, в каждом из которых изучаемая случайная величина приняла определенное значение. Предположим, что вся числовая ось разбита на несколько непересекающихся промежутков (интервалов и полуинтервалов). Обозначим через ni количество результатов измерений (значений случайной величины), попавших Отметим, что критерий c 2 будет давать удовлетворительный для практических приложений результат, если: 1) количество n опытов достаточно велико, по крайней мере 2) в каждом промежутке окажется не менее 5-10 результатов измерений, то есть
Пусть концами построенного разбиения являются точки zi, где z1<z2<…<zl-1, то есть само разбиение имеет вид
Произведем группировку для данного варианта. Объединим последние три промежутка разбиения, заменим самую левую границу разбиения на
|
|||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 285; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.149.238.67 (0.009 с.) |

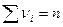 .
. ;
;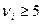 при любом i; если количество полученных значений в отдельных промежутках мало (меньше 5), то такие промежутки следует объединить с соседними, суммируя соответствующие частоты.
при любом i; если количество полученных значений в отдельных промежутках мало (меньше 5), то такие промежутки следует объединить с соседними, суммируя соответствующие частоты.
 , а самую правую на
, а самую правую на 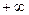 и придём к следующему интервальному распределению, пригодному для непосредственного применения критерия Пирсона:
и придём к следующему интервальному распределению, пригодному для непосредственного применения критерия Пирсона:


