
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические методы обработки экспериментальных данныхСодержание книги
Поиск на нашем сайте
Статистические методы обработки экспериментальных данных Выполнил: студент курс 2 группа форма обучения дневная Номер зачетной книжки Вариант № 14 Допущено к защите Дата защиты Результат защиты Подпись преподавателя Москва, 2009 Задание к курсовой работе 1. Выписать интервальное и точечное статистические распределения результатов наблюдений. Построить полигон и гистограмму относительных частот. 2. Найти точечные оценки математического ожидания и дисперсии. 3. Изобразить графики и выписать формулы плотностей трёх основных непрерывных распределений – нормального, показательного и равномерного. Выдвинуть гипотезу о распределении рассматриваемой случайной величины. 4. Выписать формулу теоретической плотности распределения. На одном чертеже изобразить гистограмму и график теоретической плотности, вычислив значения последней в серединах интервалов. 5. Проверить выдвинутую гипотезу о законе распределения случайной величины с помощью критерия согласия Пирсона при уровне значимости a =0,05.
Исходные данные к курсовой работе Вариант 28
Нахождение точечных оценок математического ожидания и дисперсии В качестве точечных оценок числовых характеристик изучаемой случайной величины используются: ‑ для математического ожидания
‑ для дисперсии
где n – объём выборки, ni – частота значения xi. Таким образом, в статистических расчетах используют приближенные равенства
Нахождение точечных оценок математического ожидания и дисперсии осуществим с помощью расчётной таблицы 2.
Таблица 2
Группировка исходных данных Критерий Пирсона применяется к сгруппированным данным. Предположим, что было произведено n независимых опытов, в каждом из которых изучаемая случайная величина приняла определенное значение. Предположим, что вся числовая ось разбита на несколько непересекающихся промежутков (интервалов и полуинтервалов). Обозначим через ni количество результатов измерений (значений случайной величины), попавших
Отметим, что критерий c 2 будет давать удовлетворительный для практических приложений результат, если: 1) количество n опытов достаточно велико, по крайней мере 2) в каждом промежутке окажется не менее 5-10 результатов измерений, то есть Пусть концами построенного разбиения являются точки zi, где z1<z2<…<zl-1, то есть само разбиение имеет вид
Произведем группировку для данного варианта. Объединим последние три промежутка разбиения, заменим самую левую границу разбиения на
Рис. 4 Рис. 5 Если выдвинутая гипотеза о законе распределения изучаемой случайной величины верна, то вероятность попадания значений в критическую область должна быть мала, так что событие {
называется уровнем значимости. Чтобы определить критическое значение
с неизвестной х. Поскольку распределение статистики c2 близко при n®¥ к c2 -распределению с r степенями свободы, то
и приближённое значение
Последнее уравнение имеет единственное решение: его корень – это такое число х>0, при котором площадь под графиком функции kr(t) (плотности c2 -распределения) над участком [х; +¥) равна a (рис. 5). На практике решение последнего находят при помощи специальных таблиц, позволяющих по двум входным параметрам – уровню значимости a числу степеней свободы r определить критическое значение Подводя итоги, сформулируем правило проверки гипотезы о законе распределения случайной величины с помощью c2 -критерия Пирсона: 1) Проводят n независимых наблюдений случайной величины (принято считать, что должно быть n³100).
2) Разбивают всю числовую ось на несколько (как правило, на 8-12) промежутков так, чтобы количество результатов измерений в каждом из них (называемое эмпирической частотой ni) оказалось не менее пяти. 3) Выдвигают (например, судя по профилю гистограммы) гипотезу о законе распределения изучаемой случайной величины и находят параметры этого закона (чаще всего заменяя математическое ожидание и дисперсию их оценками). 4) С помощью предполагаемого (теоретического) распределения находят теоретические вероятности pi и теоретические частоты 5) По эмпирическим и теоретическим частотам вычисляют значение статистики c2,обозначаемое как 6) Определяют число r степеней свободы. 7) Используя заданное значение уровня значимости a и найденное число степеней свободы r, по таблице находят критическое значение 8) Формулируют вывод, опираясь на основной принцип проверки статистических гипотез ‑ если наблюдаемое значение критерия принадлежит критической области, то гипотезу отвергают как плохо согласующуюся с результатами эксперимента; ‑ если наблюдаемое значение критерия принадлежит области принятия гипотезы, то гипотезу принимают как не противоречащую результатам эксперимента. Статистические методы обработки экспериментальных данных Выполнил: студент курс 2 группа форма обучения дневная Номер зачетной книжки Вариант № 14 Допущено к защите Дата защиты Результат защиты Подпись преподавателя Москва, 2009 Задание к курсовой работе 1. Выписать интервальное и точечное статистические распределения результатов наблюдений. Построить полигон и гистограмму относительных частот. 2. Найти точечные оценки математического ожидания и дисперсии. 3. Изобразить графики и выписать формулы плотностей трёх основных непрерывных распределений – нормального, показательного и равномерного. Выдвинуть гипотезу о распределении рассматриваемой случайной величины. 4. Выписать формулу теоретической плотности распределения. На одном чертеже изобразить гистограмму и график теоретической плотности, вычислив значения последней в серединах интервалов. 5. Проверить выдвинутую гипотезу о законе распределения случайной величины с помощью критерия согласия Пирсона при уровне значимости a =0,05.
Исходные данные к курсовой работе Вариант 28
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 350; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.14.131.115 (0.01 с.) |

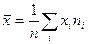 (выборочная средняя),
(выборочная средняя), (исправленная выборочная дисперсия),
(исправленная выборочная дисперсия), ,
,  .
.


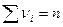 .
. ;
;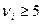 при любом i; если количество полученных значений в отдельных промежутках мало (меньше 5), то такие промежутки следует объединить с соседними, суммируя соответствующие частоты.
при любом i; если количество полученных значений в отдельных промежутках мало (меньше 5), то такие промежутки следует объединить с соседними, суммируя соответствующие частоты.
 , а самую правую на
, а самую правую на 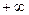 и придём к следующему интервальному распределению, пригодному для непосредственного применения критерия Пирсона:
и придём к следующему интервальному распределению, пригодному для непосредственного применения критерия Пирсона: } должно быть практически неосуществимым в единичном испытании. Эта вероятность, обозначим её через a:
} должно быть практически неосуществимым в единичном испытании. Эта вероятность, обозначим её через a: ,
, , поступим следующим образом. Зададим какое-либо малое значение уровня значимости a (как правило, a=0,05 или a=0,01) и найдём
, поступим следующим образом. Зададим какое-либо малое значение уровня значимости a (как правило, a=0,05 или a=0,01) и найдём 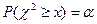

 .
.
 попадания значений случайной величины в i -й промежуток.
попадания значений случайной величины в i -й промежуток. .
.


