
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вычисление теоретических частотСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Критерий Пирсона основан на сравнении эмпирических частот с теоретическими. Эмпирические частоты ni определяются по фактическим результатам наблюдений. Теоретические частоты, обозначаемые далее через
где n – количество испытаний, а В данном варианте принята гипотеза о показательном распределении случайной величины. В этом случае теоретическая вероятность pi при любом i вычисляется по одной из следующих трёх формул (в зависимости от взаимного расположения i -го промежутка и числа x0):
Процедура отыскания теоретических вероятностей и частот показана в расчетной таблице 4.
Таблица 4 Вариант 28 (n =160; l =0,10; x0 =2,11)
5.3. Статистика c2 и вычисление её значения по опытным данным Для того чтобы принять или отвергнуть гипотезу о законе распределения изучаемой случайной величины, в каждом из критериев согласия рассматривается некоторая (специальным образом подбираемая) величина, характеризующая степень расхождения теоретического (предполагаемого) и статистического распределений. В критерии Пирсона в качестве такой меры расхождения используется величина
называемая статистикой c2 или статистикой Пирсона (вообще, статистикой называют любую функцию от результатов наблюдений). Ясно, что всегда Вычислим значение статистики c2 для данного варианта в таблице 5. Таблица 5
5.4. Распределение статистики c2 Говорят, что случайная величина имеет c2-распределение с r степенями свободы (r =1; 2; 3;…), если её плотность имеет вид:
где cr – некоторая положительная величина (cr определяется из равенства Вернёмся теперь к статистике
Если выдвинутая гипотеза верна, то, очевидно, закон распределения статистики c2 зависит только от закона распределения измеряемой случайной величины, от числа n и от выбора промежутков разбиения. Но на самом же деле в этом случае справедливо куда более сильное утверждение, а именно: при достаточно больших n закон распределения статистики c2 практически не зависит ни от закона распределения изучаемой случайной величины, ни от количества произведенных опытов: при n®¥ распределение статистики c2 стремится к c2-распределению с r степенями свободы. Эта теорема объясняет, почему статистика Пирсона обозначается через c2. Если в качестве предполагаемого выбрано одно из трёх основных непрерывных распределений, то r=l-3, где l – количество промежутков, на которые разбита числовая ось (количество групп опытных данных). В общем случае
где
|
|||||
|
Последнее изменение этой страницы: 2016-12-13; просмотров: 870; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.252.50 (0.011 с.) |

 , находят с помощью равенства
, находят с помощью равенства ,
, ‑ теоретическая вероятность попадания значений случайной величины в i -й промежуток (
‑ теоретическая вероятность попадания значений случайной величины в i -й промежуток ( ). Теоретические вероятности вычисляются в условиях выдвинутой гипотезы о законах распределения изучаемой случайной величины.
). Теоретические вероятности вычисляются в условиях выдвинутой гипотезы о законах распределения изучаемой случайной величины.

 ,
, , причём c2 =0 тогда и только тогда, когда
, причём c2 =0 тогда и только тогда, когда  при каждом i, то есть когда все соответствующие эмпирические и теоретические частоты совпадают. Во всех остальных случаях c2 ¹0; при этом значение c2 тем больше, чем больше различаются эмпирические и теоретические частоты.
при каждом i, то есть когда все соответствующие эмпирические и теоретические частоты совпадают. Во всех остальных случаях c2 ¹0; при этом значение c2 тем больше, чем больше различаются эмпирические и теоретические частоты.

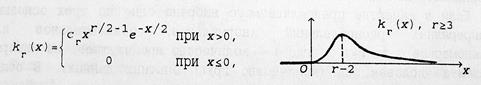
 ). Случайная величина, имеющая распределение c2 с r степенями свободы, будет обозначаться через cr2.
). Случайная величина, имеющая распределение c2 с r степенями свободы, будет обозначаться через cr2. ,
, ‑ количество параметров предполагаемого (теоретического) распределения, которые заменены вычисленными по опытным данным оценками.
‑ количество параметров предполагаемого (теоретического) распределения, которые заменены вычисленными по опытным данным оценками.


