
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование частотного модулятора.Содержание книги
Поиск на нашем сайте Теория. Система называется параметрической, если её параметры (сопротивление, индуктивности, ёмкости, взаимоиндуктивности между отдельными элементами, среда, разделяющая вход и выход, и т.д.) изменяются во времени под воздействием внешней силы, не зависящей от входного сигнала. Параметрические системы можно подразделить на строго линейные и условно линейные. К условно линейным параметрическим системам можно отнести электрические цепи, в которых управление параметрами осуществляется электронным способом. При установлении соотношений между зарядом, током и напряжением на параметрической ёмкости следует исходить из очевидных выражений.
Для параметрической индуктивности L(t) имеют место следующие соотношения, связывающие потокосцепление Ф, напряжение UL и ток i:
Системы с переменными параметрами играют очень важную роль в электросвязи. Можно говорить о двух принципиально различных видах изменения параметров канала электросвязи: а) умышленное, управляемое изменение, с целью осуществления различных преобразований сигналов (модуляция, преобразование частоты, параметрическое усиление и т.д.); б) неуправляемое изменение, обусловленное различными физическими явлениями при передаче сигналов в свободном пространстве, например, изменяющаяся во времени задержка сигнала, колебание величины затухания волн при их распространении, изменение фазовых соотношений при многолучевом распространении радиоволн, изменение сигналов во времени из-за флуктуации параметров тракта и т.д. Используя принудительное изменение во времени одного из параметров линейной цепи (апериодической) или колебательной можно получить угловую модуляцию (частотную или фазовую). В случае угловой модуляции (ЧМ и ФМ) модуляционная функция имеет вид:
При синусоидальной несущей
Реальный сигнал
Это обычное представление сигнала с угловой модуляцией. Согласно (9) полная фаза ВЧ колебания равна
а, мгновенная частота колебания изменяется по закону производной от
Наоборот, при изменении частоты по закону
В случае фазовой модуляции
При частотной модуляции по закону передаваемого сообщения изменяется частота несущего колебания
где, Полная фаза колебания при этом будет равна:
Тогда выражение ЧМ сигнала запишется в виде:
При модуляции одним током, когда U(t)=cosΩt, выражения сигнала при ФМ и ЧМ по форме имеют одинаковый вид:
где, m-индекс модуляции: при ФМ m= Для определения спектра сигнала заменим в (18) косинус суммы двух углов.
Для упрощения записи положим
…(20) где Ik(m)- бесселева функция первого рода k-го порядка от аргумента m. После подстановки (20) и (21) в (19) получаем
Таким образом, оказывается, что даже при синусоидальных ЧМ и ФМ получается теоретически безграничный спектр. Он состоит из несущей Различие между ЧМ и ФМ проявляется только при изменении частоты модуляции
Цель работы Исследование принципа действия частотного модулятора. Получение характеристик частотного модулятора при воздействии на его вход моногармонического сигнала. Исследование формы и спектра сигналов с частотной модуляцией. Схема работы и измерительная аппаратура В данной работе используется универсальный лабораторный стенд со сменным блоком ЧАСТОТНЫЙ МОДЕМ, упрощенная принципиальная схема которого приведена на рис. 8.1.
Рис. 8.1. Схема сменного блока ЧАСТОТНЫЙ МОДЕМ
Объектом исследования является левая часть схемы (между гнездами КТ1 и КТ2). Как видно из схемы, частотный модулятор представляет собой RC генератор, состоящий их двухкаскадного резистивного усилителя (А1) и фазобалансной цепи (ФБЦ), обеспечивающей положительную обратную связь. Частота генерации зависит от параметров ФБЦ (СЗ, С4) и сопротивлений каналов (RСИ) полевых транзисторов VT1 и VT2. Сопротивление канала (RСИ) зависит от управляющего напряжения, приложенного к затвору. Таким образом, полевой транзистор в ФБЦ является параметрическим элементом, управляемым модулирующим напряжением. Напряжение смещения (Есм), являющееся постоянной составляющей модулирующего сигнала, позволяет установить несущую частоту модулированного сигнала, а переменная составляющая, т.е. сам модулирующий сигнал, поданный на гнезда КТ1, обеспечивает девиацию частоты В схеме модулятора имеется блок автоматической регулировки усиления, поддерживающий постоянную амплитуду ЧМ сигнала (на схеме не показан). В качестве источника модулирующего сигнала используется встроенный диапазонный генератор, подключенный к входу модулятора. Для контроля входного сигнала используется встроенный вольтметр. Анализ спектра производится на ПК в режиме «Спектроанализатор». Домашнее задание Изучите методы детектирования ЧМ сигналов по конспекту лекций и литературе. Лабораторное задание 1. Снимите статическую модуляционную характеристику и определите оптимальный режим модулятора. 2. Определите влияние амплитуды модулирующего сигнала на форму и ширину спектра ЧМ сигнала (при постоянной частоте модуляции). 3. Определите влияние частоты модуляции на форму и ширину спектра ЧМ сигнала (при постоянной амплитуде модулирующего сигнала). 4. Наблюдайте форму сигнала на входе и выходе частотного модулятора. Методические указания 1. Статическая модуляционная характеристика (СМХ): f=
Таблица 8.1 Статическая модуляционная характеристика
По данным таблицы строится график СМХ, на котором следует отметить: - положение рабочей точки (на середине линейного участка); отсюда находят Есм opt и несущую частоту f0 (по вертикальной оси); - угол наклона линейного участка СМХ (тангенс этого угла соответствует коэффициенту Кчм модулятора); - границы линейного участка ( fmin, fmax ). Полученные данные сведем в табл. 8.2
Таблица 8.2 Оптимальный режим модулятора
В случае хорошей линейности СМХ выбор несущей частоты некритичен, однако, для последующих пунктов лучше выбрать f0= 12... 13 кГц. 2. Влияние амплитуды модулирующего сигнала на спектр ЧМ (при Fмод= const). 2.1. По ряду заданных значений Мчм (табл. 8.3) рассчитать амплитуды модулирующих сигналов, а затем и действующие значения Uc.
Таблица 8.3 Влияние амплитуды модулирующего сигнала Fмод = 500 Гц)
Для заполнения таблицы напомним некоторые определения для ЧМ. Индекс частотной модуляции
Отсюда находят Δ fmax. Определение ЧМ сигнала: При амплитудном значении гармонического сигнала Umc
Отсюда Четвертая строка таблицы заполняется исходя из необходимости пользоваться вольтметром переменного напряжения, имеющим градуировку в действующих значениях: Uc = Umc 0,707. 2.2. Подключить внутренний звуковой генератор ко входу модулятора (гнездо КТ1). Туда же подключить и вольтметр переменного напряжения стенда. Установить частоту генератора Fмод = 500 Гц. 2.3. Последовательно устанавливая значения Uc из табл. 8.3 регулятором выхода генератора, получить на ПК, подключенном к выходу модулятора (гнездо КТ2) спектры ЧМ сигналов. На каждой спектрограмме обязательно указывать: • условия проведения эксперимента; • частоты отдельных составляющих спектра; • практическую ширину спектра 2Δ f *(при определении 2Δ f * учитывать только ту часть спектра, в которой амплитуды указывать не менее 10% от максимальных амплитуд). Полученные значения 2Δ f *внести в табл. 8.3 3. Влияние частоты модуляции на спектр ЧМ сигнала ( Uc=const )/ 3.1. Сохраняя схему соединений (п.2), установить значения Uc из табл. 8.3 для Мчм = 2,4 и не менять его в дальнейшем. 3.2. Последовательно устанавливая частоты модуляции (табл. 8.4), получить спектрограммы соответствующих ЧМ сигналов. В таблицу внести значения 2Δ f *.
Таблица 8.4 Влияние частоты модуляции (Uc = const)
3.3. Заполнить последнюю строку табл. 8.4, используя определение Мчм и необходимые данные из табл. 8.3. 4. Форма колебаний на входе и выходе частотного модулятора. 4.1. Соединить один из входов двухлучевого осциллографа с входом модулятора (для этого надо отключить вольтметр, сохраняя соединение с генератором). На другой вход осциллографа подать выходной сигнал модулятора. 4.2. Установить частоту модуляции Fмод=300 Гц, а уровень сигнала увеличивать до тех пор, пока на осциллограмме выходного сигнала не появится паразитная амплитудная модуляция. Несколько уменьшить входной сигнал так, чтобы огибающая ЧМ сигнала стала ровной. 4.3. Установить синхронизацию осциллографа по тому каналу (входу), на который подан низкочастотный (входной) сигнал. Ручками синхронизации добиться неподвижного изображения. 4.4. Синхронизация выходной осциллограммы частотного модулятора достигается небольшой подстройкой несущей частоты (ручкой СМЕЩЕНИЕ). 4.5. Зафиксировать осциллограммы на входе и выходе частотного модулятора. Отчет Отчет должен содержать: 1) схему частотного модулятора; 2) статическую модуляционную характеристику; 3) спектры, таблицы и осциллограммы по всем пунктам исследований; 4) теоретический расчет спектров для: • п.2.1, при Мчм = 2,4 (из табл. 8.3), • п.3.1, при Fмод - 250 Гц (из табл. 8.4). Для расчетов принять Um0 = 1 В (амплитуда немодулированного сигнала); 5) выводы по пп. 2 и 3.
Контрольные вопросы
1. Дайте определение ЧМ- колебания. 2. Приведите пример записи тонального ЧМ- колебания с параметрами f0 = 100 МГц;, Fмод = 10 кГц; Δfmax - 50 кГц. 3. Опишите принцип действия частотного модулятора. Какие способы получения ЧМ- колебаний Вам известны? 4. Дайте определение статической модуляционной характеристики и поясните ее смысл. 5. Что такое угловая модуляция? 6. Как рассчитать спектр ЧМ- колебания? 7. Представьте (качественно) спектр колебания
8. Какое отношение имеют функции Бесселя к частотной модуляции? 9. Сколько спектральных линий надо учесть в практической ширине спектра ЧМ при Мчм = 4? 10. Назовите известные Вам области применения ЧМ сигналов.
Лабораторная работа №9
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 1280; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |

 … (1)
… (1)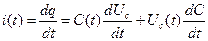 … (2)
… (2) … (3)
… (3) … (4)
… (4) … (5)
… (5) … (6)
… (6) … (7)
… (7) модулированный сигнал имеет следующее выражение:
модулированный сигнал имеет следующее выражение: … (8)
… (8)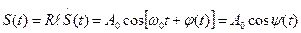 … (9)
… (9) … (10)
… (10) т.е.
т.е.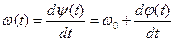 … (11)
… (11) -(11), фаза колебаний
-(11), фаза колебаний  будет изменяться по закону интеграла от
будет изменяться по закону интеграла от 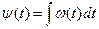 … (12)
… (12) . Тогда, на основании (9) и (10) имеем:
. Тогда, на основании (9) и (10) имеем: … (13)
… (13) … (14)
… (14) … (15)
… (15) - амплитуда частотного отклонения (девиация частоты).
- амплитуда частотного отклонения (девиация частоты). … (16)
… (16) … (17)
… (17) … (18)
… (18) , а при ЧМ
, а при ЧМ  .
. … (19)
… (19) . Из теории бесселевых функций известны следующие соотношения:
. Из теории бесселевых функций известны следующие соотношения: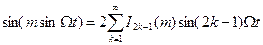
 … (21)
… (21)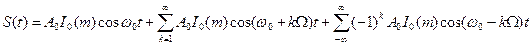 … (22)
… (22) и двух боковых полос
и двух боковых полос  . Амплитуда несущей A0I0(m), при ЧМ и ФМ, в отличие от АМ, зависит от модулирующего колебания. Амплитуда боковых частот равна Ak = A0Ik(m). Однако практически ширина спектра ЧМ и ФМ ограничена. Практически ширина спектра сигнала при угловой модуляции равна F=2(m+1)Fm, где
. Амплитуда несущей A0I0(m), при ЧМ и ФМ, в отличие от АМ, зависит от модулирующего колебания. Амплитуда боковых частот равна Ak = A0Ik(m). Однако практически ширина спектра ЧМ и ФМ ограничена. Практически ширина спектра сигнала при угловой модуляции равна F=2(m+1)Fm, где  - частота модулирующего сигнала.
- частота модулирующего сигнала. . При ЧМ
. При ЧМ  , поэтому при m>>1 полоса
, поэтому при m>>1 полоса  практически не зависит от Fm. При ФМ
практически не зависит от Fm. При ФМ  и при m>>1ширина спектра будет равна 2
и при m>>1ширина спектра будет равна 2  , т.е. она зависит от модулирующей частоты Fm. В этом и состоит различие в спектрах ЧМ и ФМ.
, т.е. она зависит от модулирующей частоты Fm. В этом и состоит различие в спектрах ЧМ и ФМ.
 fmax, зависящую от амплитуды модулирующего сигнала. Выходом частотного модулятора являются гнезда КТ2.
fmax, зависящую от амплитуды модулирующего сигнала. Выходом частотного модулятора являются гнезда КТ2.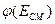 снимается при отсутствии модулирующего сигнала. Последовательно устанавливая движковым потенциометром Eсм значения из табл. 8.1, определить значения частоты модулятора f подключив выход модулятора (гнездо КТ2) к входу ПК, работающего в режиме анализа спектра (см. приложение).
снимается при отсутствии модулирующего сигнала. Последовательно устанавливая движковым потенциометром Eсм значения из табл. 8.1, определить значения частоты модулятора f подключив выход модулятора (гнездо КТ2) к входу ПК, работающего в режиме анализа спектра (см. приложение).







