
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Исследование детектора ЧМ сигналов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Теория
Приём частотно-модулированных сигналов более свободен от атмосферных и промышленных помех, благодаря чему повышается качество воспроизведения. При частотной модуляции амплитуда ВЧ колебаний остаётся постоянной, а в соответствии с передаваемым сигналом изменяется частота ВЧ колебаний Напряжение на выходе частотного детектора должно воспроизводить закон изменения мгновенной частоты модулированного колебания. Представив последнее в форме
получим для идеального частотного детектора следующую функциональную связь:
где SЧД=const- крутизна характеристики детектора, выраженная в вольтах на единицу угловой частоты;
крутизна характеристики SЧД имеет размерность Предполагается, что ∆f(t), а следовательно, и Uвых(t) являются “медленными” функциями времени. Для выделения сообщения из частотно-модулированного колебания, спектр которого состоит только из высокочастотных составляющих (несущая частота
Рис.9.1 Схема частотного детектирования
рис. 9.2. Преобразование ЧМ в АМ с помощью колебательного контура. Если резонансная частота контура Положение точек Изменение амплитуды Uk высокочастотного напряжения с помощью диода VД преобразуется в низкочастотное напряжение, которое выделяется на апериодической нагрузке RфСф. в исходном положении, т.е. в отсутствии модуляции, рабочая точка должна устанавливаться на скате резонансной кривой. Детектор с одиночным контуром имеет ограниченный линейный участок резонансной кривой. Значительно больший участок может быть получен от дифференциальной схемы, в которой используется две параллельно соединенные схемы с одиночными контурами. Один из контуров настраивается на частоту Существенным недостатком схемы с двумя расстроенными контурами является настройка контуров на частоты, отличные от частоты Такие схемы широко применяются в приёмниках ЧМ сигналов и в схемах автоподстройки частоты генераторов.
Цель работы Экспериментальное исследование частотного детектора. Выбор оптимального режима детектирования. Схема работы и используемая аппаратура В данной работе используется универсальный лабораторный стенд со сменным блоком ЧАСТОТНЫЙ МОДЕМ (рис.8.1). В качестве источника ЧМ сигнала в данной работе используется частотный модулятор, рассмотренный в лабораторной работе 8. Выход частотного модулятора (гнездо КТ2 на рис. 8.1) соединяется перемычкой с входом частотного детектора (гнездо КТЗ). Выход частотного детектора (гнездо КТ4) соединен с микроамперметром, измеряющим постоянную составляющую тока детектора. Схема частотного детектора состоит из усилителя на полевом транзисторе VT3, в нагрузку которого включены два резонансных контура, настроенных на разные частоты (f01 и f02). Эти частоты расположены симметрично относительно несущей частоты ЧМ сигнала. Ток ЧМ сигнала с постоянной амплитудой, протекая через два расстроенных контура, вызывает на них падения напряжения, пропорциональные их сопротивлениям. Чем ближе мгновенная частота ЧМ сигнала к резонансной частоте контура, тем больше амплитуда напряжения на контуре и наоборот. Таким образом, линейная цепь (рассмотренный колебательный контур) преобразует ЧМ сигнал в сигнал, в котором и амплитуда и частота меняются одновременно. Осциллограмма такого сигнала внешне очень похожа на AM сигнал, но частота заполнения его меняется так же, как у входного ЧМ сигнала. Нагрузкой каждого контура является свой детектор огибающей (AM детектор). Выходные напряжения AM детекторов (на резисторах R5 и R6) зависят от расстройки контуров относительно мгновенной частоты ЧМ сигнала. Для идеальной работы ЧМ детектора модуль полного сопротивления расстроенного контура должен меняться прямо пропорционально девиации частоты ЧМ сигнала. Однако на частотной характеристике контура имеется небольшой почти линейный участок в районе точки перегиба. Для увеличения ширины линейного участка характеристики детектирования применяют не один, а два симметрично расстроенных контура. Встречное включение диода (VD2) во втором детекторе огибающей позволяет в значительной степени компенсировать нелинейность склона АЧХ контура, а также компенсировать постоянную составляющую выходного сигнала. Выходное напряжение ЧМ детектора (гнездо КТЗ) равно разности напряжений на выходах AM детекторов: Uвых = UR5 - UR6 В работе также используются встроенные звуковой генератор, приборы постоянного и переменного напряжений, двухлучевой осциллограф и ПК, используемый как частотомер или анализатор спектра. Домашнее задание 1. Изучите методы дискретизации и квантования непрерывных сигналов по конспекту лекций и литературе. Лабораторное задание 1. Снимите характеристику детектирования и выберите оптимальный режим работы частотного детектора. 2. Наблюдайте сигналы на входе модулятора и выходе детектора в оптимальном режиме и при отклонениях от него. Методические указания 1. Снятие характеристики детектирования I0 = Процесс измерения характеристики детектирования существенно упрощается, если на этом же стенде уже выполнена работа 8. В этом случае необходимость в измерении частот отпадает и первые две строчки из табл. 8.1 переносятся в табл. 9.1. 1.1. Изменяя напряжение смещения (ЕCM.)в соответствии с табл. 9.1, измерить с помощью ПК (в режиме «Спектроанализатор») частоты модулятора и, одновременно с этим, ток детектора I0.
Таблица 9.1 Снятие статической модуляционной характеристики f=
При заполнении табл. 9.1 кроме указанных значений ЕСМследует добавить те значения Есми f, при которых I0 принимает нулевое и экстремальные значения. 1.2. По результатам табл. 9.1 строится статическая модуляционная характеристика (СМХ) и характеристика детектирования (ХД). Из графика ХД определить оптимальное значение несущей частоты f0, соответствующее нулевому току детектора и максимальную девиацию частоты Δfmax соответствующую границе линейного участка ХД, считая от частоты f0. Из СМХ определяют напряжение смещения Есм opt, при котором несущая частота равна f0, и максимальную амплитуду сигнала Uмс, при которой девиация частоты составит полученные значения параметров внести в табл. 9.2.
Таблица 9.2 Оптимальный режим частотного детектора
1.3. Соединить выход звукового генератора с гнездом КТ1 (вход модулятора). Туда же подключить вольтметр переменного напряжения. Установить на генераторе гармонический сигнал с частотой FMOД = 200 Гц и действующим значением Uc max (по вольтметру). Установить Есм = Есм opt. (из табл. 9.2). 1.4. Заменить вольтметр на входе 1 на один из входов двухлучевого осциллографа, а второй его вход соединить с выходом детектора (гнездо КТ4). 1.5. Получив неподвижные осциллограммы, зафиксировать их в отчете. Обратить внимание на «зубцы» выходной осциллограммы, связанные с работой амплитудных детекторов. 2. Работа детектора в неоптимальном режиме изучается при выходе сигнала за пределы линейного участка ХД. 2.1. Изменить напряжение смещения на +0,5 В от оптимального. По графику СМХ или табл. 9.1 определить новое значение несущей частоты и внести его в отчет. Повторить п. 1.5. 2.2. Повторить п.2.1, но при Есм=Есм opt — 0,5 В. 2.3. Восстановить прежнее значение Ecм opt. Увеличить модулирующий сигнал Uc в 1,5 раза. (Для этого на время измерения заменить вход осциллографа, подключенный к гнезду 1, на вольтметр). Повторить п. 1.5. Отчет Отчет должен содержать: 1) принципиальную схему частотного детектора; 2) статическую модуляционную характеристику частотного модулятора; 3) характеристику детектирования; 4) временные диаграммы оптимального и неоптимального режимов. Контрольные вопросы 1. Дайте определение ЧМ сигнала. 2. Запишите выражение сигнала с тональной частотной модуляцией. 3. Амплитуда несущего колебания и амплитуда немодулированного ЧМ сигнала - это одно и то же или нет? 4. Тот же вопрос для АМ- сигнала. 5. Что такое Мчм и Кчм? 6. Какие требования предъявляются к частотному модулятору и частотному детектору? 7. Какие функции выполняют частотный модулятор и частотный детектор? 8. Как работает частотный детектор? 9. Где применяется частотная модуляция? 10. Какое отношение имеет функция Бесселя к спектру ЧМ сигнала? 11. Что такое оптимальный режим частотного детектора? Лабораторная работа № 10 Дискретизация непрерывных сигналов во времени (теорема Котельникова) Суть дискретизации по времени состоит в том, что непрерывное сообщение заменяется последовательностью его мгновенных значений (отсчетов), взятых в дискретных точках времени (рис. 10.1). При такой замене из рассмотрения исключается все множество значений непрерывной функции времени, находящихся внутри интервалов времени
Рисунок 10.1 Дискретизация по времени может быть равномерной (принудительной), когда интервал дискретизации Наиболее широко применяется равномерная дискретизация. Теория и техника такой дискретизации достаточно хорошо разработаны, она сравнительно проста и удобна для решения многих задач. В частности, равномерная дискретизация может использоваться (и используется) как промежуточная операция при решении задач адаптивной дискретизации, сжатия сообщений для устранения в них избыточности, временного уплотнения каналов в системах связи и т. п. В основе математического описания дискретизации непрерывных функций по времени лежит так называемая импульсная функция дискретизации aД(t), которая представляет собой периодическую последовательность -функций (единичных импульсных функций), следующих через интервалы времени
(1) Такую функцию можно назвать также периодической стробирующей или коммутационной импульсной функцией. Используя преобразование Фурье, можно показать, что спектр импульсной функции дискретизации определяется выражением
которое представляет собой периодическую последовательность -функций, следующих через частотные интервалы
площадь каждой составляющей в выражении (3) равна единице, Дискретизация непрерывной функции времени x(t) с математической точки зрения представляет собой умножение этой функции на функцию ад (t):
В соответствии с фильтрующим свойством
имеем
Это выражение означает, что умножение функции x(t) на единичный С учетом (6) выражение (4) принимает вид
Следовательно, умножение сообщения x(t) на импульсную функцию дискретизации приводит к образованию периодической последовательности На практике реализовать импульсную функцию дискретизации в виде Практическую реализацию дискретизации по времени часто называют импульсным преобразованием непрерывного сообщения. По сути дела такое преобразование эквивалентно получению амплитудно-модулированной последовательности импульсов (АИМ). При решении задач дискретизации непрерывных сообщений по времени, возникает ряд вопросов: 1) из каких соображений необходимо исходить при выборе интервала дискретизации 2) какова точность замены непрерывного сообщения последовательностью его отсчетов, взятых в дискретные моменты времени, и от чего она зависит; 3) каков максимально допустимый интервал дискретизации Получить ответ на эти и другие вопросы можно лишь в случае, если проблему дискретизации по времени рассматривать в неразрывной связи с обратной проблемой - восстановлением непрерывной функции времени по ее мгновенным значениям, известным только в дискретные моменты времени. Сложность этой проблемы состоит в том, что нужно восстановить утраченные при дискретизации сведения о поведении непрерывной функции времени в промежутках между отсчетами. Очевидно, что чем меньшим количеством отсчетов заменяется сообщение длительностью Тс,тем продолжительнее интервал дискретизации Таким образом, рассматриваемая проблема дискретизации не имеет однозначного решения. Осуществление более экономного импульсного преобразования непрерывного сообщения связано с усложнением задачи восстановления этого сообщения по его отсчетам. И наоборот, неэкономное (избыточное) импульсное преобразование приводит к упрощению процедуры восстановления. При реализации импульсного преобразования приходится принимать компромиссное решение, учитывающее отмеченные выше особенности. Выбор интервала дискретизации В теории дискретизации непрерывных сообщений особую важность приобретает вопрос о максимальном (предельном) интервале дискретизации
где скобки указывают на то, что берется целая часть отношения. Дискретизацию непрерывных сообщений, соответствующую такому условию, назовем предельной. Она обеспечивает представление непрерывного сообщения с заданной точностью минимальным (безызбыточным) количеством отсчетов. Проблема предельной дискретизации сложна и, несмотря на значительное количество исследований, далека от завершения. Большое внимание, которое уделяется теории предельной дискретизации по времени, объясняется тем, что она лежит в основе анализа ряда важнейших вопросов преобразования и передачи непрерывных сообщений, в частности, при исследовании вопросов устранения избыточности сообщений («сжатие информации»), пропускной способности каналов и т. п. В настоящее время наиболее разработанной и широко применяемой предельной дискретизацией непрерывных сообщений является дискретизация, основанная на теореме Котельникова. Остановимся на исходных положениях этой теоремы. Как уже указывалось выше, при построении теории дискретизации необходимо опираться на некоторую модель сообщения. Допустим, что нам известна одна из реализаций x(t) квазистационарного случайного процесса x(t), соответствующего совокупности возможных непрерывных сообщений. Как бы сложно эта реализация ни выглядела, она представляет собой некоторую неслучайную (детерминированную) функцию времени. Пользуясь преобразованием Фурье, можно найти комплексный амплитудный спектр этой функции:
Если функция x(t) задана графически в виде фотограммы или существует в виде записи на магнитную ленту, можно воспользоваться одним из известных методов вычислительной математики и построить график амплитудного спектра. Исходя из требуемой точности и допустимого уровня помех, ограничим этот спектр некоторой частотой Для такой модели верна следующая теорема: если непрерывная функция времени х(t) имеет спектр, ограниченный полосой частот от нуля до Fb, to эта функция полностью определяется последовательностью своих мгновенных значений, взятых в моменты времени, отсчитываемые через интервалы Эта теорема как математическое положение установлена давно. Однако в наиболее четкой форме ее сформулировал, доказал и применил к конкретным проблемам передачи сообщений В. А. Котельников в 1933 г. Поэтому вполне справедливо в отечественной литературе указанную теорему называют теоремой Котельникова. В иностранной литературе (в основном американской и английской) подобную теорему обычно называют теоремой отсчетов или теоремой Найквиста. Доказательство теоремы Котельникова содержится в ряде книг. Результатом доказательства теоремы является выражение (9):
Разложение непрерывной функции времени x(t) в ряд вида (9) очень важно и приобрело в теории информации и других областях не меньшее значение, чем разложение Фурье. В этом разложении значения x(k
Sin Тогда выражение (9) можно рассматривать как частный случай обобщенного ряда Фурье:
Принципиальная важность выражения (3.8) заключается в том, что оно дает решение как прямой задачи (выбор интервала дискретизации Если у сообщения длительностью Тс ограничить спектр на частоте FВ, то в соответствии с теоремой Котельникова можно обра
(11) В этом случае ряд (10) будет содержать конечное число членов и, следовательно, представление непрерывной функции таким рядом будет неточным:
Приближенность этого выражения проявляется в том, что при конечном числе членов ряда их сумма точно совпадает с мгновенными значениями функции x(t) не на всем интервале времени Тс, а только в точках отсчетов. В интервалах между точками отсчета значения функции x(t) и функции приближения Таким образом, дискретизация непрерывного сообщения конечной длительности в соответствии с теоремой Котельникова связана с ошибкой, одна составляющая которой обусловлена введением модели с ограниченным спектром, а вторая — учетом конечного числа членов ряда разложения. Восстановление непрерывной функции времени с конечной длительностью по ее отсчетам должно выполняться в соответствии с выражением (9). Эта процедура может быть выполнена двумя способами: фильтрационным, с применением аналогового фильтра и интерполяционным, с применением специальных интерполяторов или универсальных вычислительных машин. Рассмотрим кратко суть этих способов. При фильтрационном способе восстановления, последовательность отсчетов, определяемая выражением (9), в котором интервал дискретизации в соответствии с теоремой Котельникова равен
Этой функции соответствует фильтр нижних частот с прямоугольной передаточной функцией. Как известно, такой фильтр физически нереализуем. При интерполяционном способе процедура восстановления должна выполняться в соответствии с выражением (9), которое можно рассматривать как алгоритм этой процедуры. В соответствие с этим алгоритмом необходимо создать m=2FBTc функций вида
и просуммировать их с учетом весовых коэффициентов, равных переданным отсчетам хk=x(k Цель работы Исследование процессов дискретизации и восстановления непрерывных сигналов. Схема работы и измерительная аппаратура Исследуемое устройство (рис.10.1) размещено на сменном блоке ТЕОРЕМА КОТЕЛЬНИКОВА и представляет собой дискретизатор (обозначенный на макете как перемножитель сигналов) и набор из трех фильтров — восстановителей с разными частотами среза. Источники исследуемых сигналов S1, S2 и S3находятся в блоке ИСТОЧНИКИ СИГНАЛОВ, а сами сигналы представляют собой суммы гармоник с частотами 2, 4 и 6 кГц. (При необходимости исследуемый сигнал может быть усложнен добавлением еще одного гармонического сигнала с. частотой 1 кГц с помощью сумматора стенда.) Дискретизатор, формирующий отсчеты S(kΔt) непрерывного сигнала S(t), выполняет
Рис. 10.1 Сменный блок ДИСКРЕТИЗАЦИЯ НЕПРЕРЫВНЫХ СИГНАЛОВ ВО ВРЕМЕНИ (теорема Котельникова) функцию перемножителя этого сигнала на короткие импульсы напряжения дискретизации (ил). В данном случае дискретизатор выполнен по схеме аналогового коммутатора, пропускающего входной сигнал S(t) на выход в течение короткого времени существования импульсов дискретизации. Временной интервал между соседними отсчетами дискретизированного сигнала S(kΔt) зависит от выбора частоты дискретизации fд: Δt=1/fд. Эта частота может изменяться дискретно при нажатии кнопки fд, при этом выбранное значение этой частоты индицируется светодиодом (fд =3, 6, 12, 16, 24 и 48 кГц). Все упомянутые выше частоты (частоты дискретизации и частоты гармоник исследуемых сигналов) жестко синхронизированы, что упрощает наблюдение процессов на осциллографе. В качестве фильтров-восстановителей используются три активных ФНЧ четвертого порядка с частотами среза 3, 6 и 12 кГц. Для снятия импульсных характеристик фильтров используется генератор коротких импульсов В соответствии с теоремой Котельникова отсчеты, следующие через интервалы времени Δt = 1/2fB где fB - верхняя частота сигнала, могут быть преобразованы в исходный сигнал после прохождения через идеальный ФНЧ с частотой среза fср = fB. В работе используются реальные ФНЧ с достаточно крутыми спадами АЧХ после частоты среза. Исходя из этого, на практике выбирают Δt несколько меньше (а иногда и в несколько раз меньше), чем требуется в теореме Котельникова с тем, чтобы реальный ФНЧ с АЧХ трапециевидной формы позволял выделить спектр исходного сигнала из спектра дискретизированного сигнала, что гарантирует отсутствие искажений при обратном преобразовании (восстановлении) сигнала. В качестве измерительных приборов используются двулучевой осциллограф и ПК, работающий в режиме анализатора спектра. Домашнее задание Изучите раздел «Дискретизация непрерывных сигналов во времени» по конспекту лекций. Лабораторное задание 1. Произведите дискретизацию одного из сложных сигналов (S1,S2 или Sз). 2. Исследуйте спектры исходного и дискретизированного сигналов. 3. Исследуйте частотные и импульсные характеристики фильтров-восстановителей. 4. Исследуйте процесс восстановления дискретизированных сигналов. Методические указания 1. Дискретизация сигнала. 1.1. Выбрать один из трех сигналов (например, S1) в блоке ИСТОЧНИКИ СИГНАЛОВ и подать его на вход «А» ПК, работающего в режиме спектроанализатора. (Входы ПК находятся в нижней части стенда справа.) 1.2. С помощью спектроанализатора (ПК) получить спектр сигнала и определить его верхнюю частоту (FB). 1.3. Учитывая, что значения частот дискретизации (fд), указанных на сменном блоке, являются ориентировочными, провести спектральный анализ сигналов UД (гнездо под перемножителем). Определив частоты первых гармоник этих сигналов при установке fД = 3, 6, 12 и 16 кГц, внести уточненные значения в табл. 10.1. Для частот более 24 и 48 кГц спектральный анализ в данной работе невозможен (так как Fmax=24 кГц), поэтому их следует умножить на тот же коэффициент, который связывает указанные на блоке и уточненные значения частот дискретизации. (Этот коэффициент (
Таблица 10.1 Уточненные частоты дискретизации (fД)
1.4. Рассчитать требуемую частоту дискретизации fД и установить ее на макете кнопкой fД. 1.5. Соединить входы двулучевого осциллографа с входом и выходом дискретизатора, установить режим внешней синхронизации осциллографа (от гнезда С1 блока ИСТОЧНИКИ). Вход спектроанализатора подключить к выходу дискретизатора. 1.6. Зафиксировать в отчете временные диаграммы в следующем порядке (с сохранением масштаба по оси времени) • исследуемый сигнал S(t); • напряжение дискретизации (гнездо нижнего входа перемножителя); • выходной дискретизированный сигнал S(kΔt). С экрана монитора ПК зарисовать спектры перечисленных выше сигналов. 1.7. Переключая кнопкой частоту дискретизации fД на 1-2 шага выше и ниже выбранного значения fД, наблюдать изменения в осциллограммах и спектрах на выходе дискретизатора. Наиболее характерные случаи зафиксировать в отчете. 2. Исследование фильтров. С целью выбора наилучшего из трех ФНЧ в качестве фильтра-восстановителя необходимо определить частоту среза каждого из них по АЧХ либо по импульсной характеристике g(f). Кроме того, АЧХ фильтров не
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-07-16; просмотров: 1036; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.84.128 (0.017 с.) |

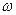 . Изменение частоты
. Изменение частоты  при неискажённой модуляции должно быть пропорционально амплитуде модулирующего сигнала.
при неискажённой модуляции должно быть пропорционально амплитуде модулирующего сигнала. , … (1)
, … (1) , … (2)
, … (2) - мгновенное значение частотного отклонения входной ЭДС. Если пользоваться частотами
- мгновенное значение частотного отклонения входной ЭДС. Если пользоваться частотами  , то в выражении
, то в выражении , … (3)
, … (3) .
. и боковые частоты модуляции), необходимо нелинейное устройство. Следовательно, частотный детектор обязательно должен включать в себя нелинейный элемент. Однако, в этом случае в отличие от амплитудного детектора для выделения частот сообщения одного лишь нелинейного элемента недостаточно. Из рассмотрения вольтамперных характеристик нелинейных элементов видно, что при постоянстве амплитуды входного напряжения нелинейный элемент не реагирует на изменение частоты этого напряжения. Нелинейность таких устройств, как диод, триод и т.п., проявляется лишь при изменении величины действующего на них напряжения, а не при изменении частоты или, в общем случае, скорости изменения сигнала. Обычный частотный детектор представляет собой сочетание двух основных частей:1) избирательной линейной системы, преобразующей частотную модуляцию в амплитудную, и 2) амплитудного детектора. Так как при преобразовании высокочастотного сигнала в сигналы промежуточной частоты наблюдается паразитная амплитудная модуляция ЧМ сигнала, то перед линейной избирательной системой устанавливают ограничитель амплитуды ЧМ сигнала. В качестве линейной системы может использоваться колебательный контур. Схема частотного детектора, содержащего простой колебательный контур, представлена на рис.9.1.
и боковые частоты модуляции), необходимо нелинейное устройство. Следовательно, частотный детектор обязательно должен включать в себя нелинейный элемент. Однако, в этом случае в отличие от амплитудного детектора для выделения частот сообщения одного лишь нелинейного элемента недостаточно. Из рассмотрения вольтамперных характеристик нелинейных элементов видно, что при постоянстве амплитуды входного напряжения нелинейный элемент не реагирует на изменение частоты этого напряжения. Нелинейность таких устройств, как диод, триод и т.п., проявляется лишь при изменении величины действующего на них напряжения, а не при изменении частоты или, в общем случае, скорости изменения сигнала. Обычный частотный детектор представляет собой сочетание двух основных частей:1) избирательной линейной системы, преобразующей частотную модуляцию в амплитудную, и 2) амплитудного детектора. Так как при преобразовании высокочастотного сигнала в сигналы промежуточной частоты наблюдается паразитная амплитудная модуляция ЧМ сигнала, то перед линейной избирательной системой устанавливают ограничитель амплитуды ЧМ сигнала. В качестве линейной системы может использоваться колебательный контур. Схема частотного детектора, содержащего простой колебательный контур, представлена на рис.9.1.
 отличается от средней частоты
отличается от средней частоты  , а второй- на частоту
, а второй- на частоту  . При этом изменение частоты
. При этом изменение частоты  производится при отсутствии модулирующего сигнала (Мчм=0) путем изменения частоты входного сигнала с измерением постоянной составляющей тока детектора. При этом вход модулятора отключен (гнездо КТ1 свободно), между гнездами КТ2 и КТЗ установлена перемычка, а управление частотой осуществляется изменением смещения (Есм) в модуляторе. Измерение частоты на выходе модулятора (гнездо КТ2) производится с помощью ПК в режиме «Спектроанализатор», а измерение тока I0 - с помощью микроамперметра, расположенного над регулятором ЕCM.
производится при отсутствии модулирующего сигнала (Мчм=0) путем изменения частоты входного сигнала с измерением постоянной составляющей тока детектора. При этом вход модулятора отключен (гнездо КТ1 свободно), между гнездами КТ2 и КТЗ установлена перемычка, а управление частотой осуществляется изменением смещения (Есм) в модуляторе. Измерение частоты на выходе модулятора (гнездо КТ2) производится с помощью ПК в режиме «Спектроанализатор», а измерение тока I0 - с помощью микроамперметра, расположенного над регулятором ЕCM. и характеристики детектирования I0=
и характеристики детектирования I0=  t. Полученная при этом функция имеет вид последовательности отсчетов, взятых в дискретные моменты времени. Часто такую функцию называют решетчатой.
t. Полученная при этом функция имеет вид последовательности отсчетов, взятых в дискретные моменты времени. Часто такую функцию называют решетчатой.

 (2)
(2) -функций
-функций
 (4)
(4) (5)
(5)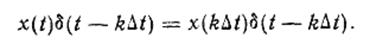 (6)
(6) (7)
(7) . Если выбрать величину
. Если выбрать величину  , образуется последовательность коротких импульсов, амплитуды которых пропорциональны мгновенным значениям сообщения.
, образуется последовательность коротких импульсов, амплитуды которых пропорциональны мгновенным значениям сообщения.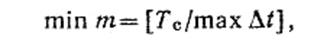
 (8)
(8)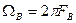 , т.е. введем модель сообщения с ограниченным амплитудным спектром. Введенная модель характеризуется следующими особенностями: 1) относится к одной реализации случайного процесса, т. е. соответствует детерминированной функции; 2) имеет ограниченный спектр.
, т.е. введем модель сообщения с ограниченным амплитудным спектром. Введенная модель характеризуется следующими особенностями: 1) относится к одной реализации случайного процесса, т. е. соответствует детерминированной функции; 2) имеет ограниченный спектр.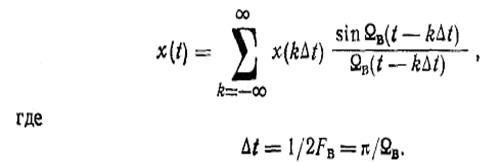
 - как базисные функции
- как базисные функции 
 (10)
(10) с весовыми коэффициентами, равными отсчетам xk. Это означает, что точное восстановление функции x(t) с ограниченным спектром возможно только при бесконечной протяженности этой функции во времени. В действительности же все реальные сообщения имеют ограниченную продолжительность во времени. Характерной особенностью реальных сообщений является то, что они относятся к такому классу функций, у которых почти вся энергия сосредоточена в конечных интервалах времени и полосы частот.
с весовыми коэффициентами, равными отсчетам xk. Это означает, что точное восстановление функции x(t) с ограниченным спектром возможно только при бесконечной протяженности этой функции во времени. В действительности же все реальные сообщения имеют ограниченную продолжительность во времени. Характерной особенностью реальных сообщений является то, что они относятся к такому классу функций, у которых почти вся энергия сосредоточена в конечных интервалах времени и полосы частот. зовать число отсчетов, равное:
зовать число отсчетов, равное: (12)
(12) (t) различаются и появляется погрешность. Уменьшить эту погрешность можно путем увеличения числа членов ряда. Как следует из выражения (11), при конечной длительности сообщения Тс это можно сделать, только уменьшая интервал дискретизации
(t) различаются и появляется погрешность. Уменьшить эту погрешность можно путем увеличения числа членов ряда. Как следует из выражения (11), при конечной длительности сообщения Тс это можно сделать, только уменьшая интервал дискретизации  t, т. е. увеличивая значение частоты FB, которой ограничивается спектр сообщения.
t, т. е. увеличивая значение частоты FB, которой ограничивается спектр сообщения.


 1,15) может быть уточнен по первым четырем значениям. fД)
1,15) может быть уточнен по первым четырем значениям. fД)


