Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Характеристики электрических сигналов электросвязи.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Для передачи сообщений в электросвязи и радиотехнике применяются специальные электрические колебания, называемые электрическими сигналами Информация, заключённая в сигнале, полезна в том случае, когда передаваемое сообщение заключает в себе что-то новое, непредвиденное. Следовательно, сигнал в аналитическом отношении должен представляться получателю случайной функцией времени. Электрический сигнал представляет собой физический (электрический процесс), несущий в себе информацию. Количество информации, переданное с помощью сигнала, зависит от его основных параметров: длительности, полосы частот, мощности и некоторых других характеристик. Сигналы подразделяются на детерминированные (определённые), и случайные. Детерминированным называется любой сигнал, параметры и мгновенное значение которого в любой момент времени могут быть предсказаны с вероятностью единица. Детерминированные сигналы подразделяются на периодические и непериодические. Периодическим называется любой сигнал, для которого выполняется условие S(t)=S(t+kT), где период Т - является конечным отрезком времени, а k- любое целое число. Простейшим, периодически детерминированным сигналом, является гармоническое колебание (ток, напряжение, заряд, напряжённость поля), определяемое законом:
при Непериодическим детерминированным сигналом, называется любой детерминированный, для которого не выполняется условие S(t)=S(t+kT). Непериодический сигнал ограничен во времени, он чаще всего используется в практике. Основной характеристикой периодических и непериодических сигналов является их спектральная функция. Строго гармоническое колебание, называют моногармоническим. Спектр такого колебания состоит из одной спектральной линии. Колебание имеет форму синусоиды с определённым периодом Т. Анализ периодических сигналов и цепей связи производится временным и спектральным способом. Спектральный способ основан на разложении сигналов в тригонометрический ряд Фурье. Цель временного анализа - определить изменение формы сигнала по отклику (реакции) цепи на оказываемое на неё воздействие. Спектральный способ позволяет выявить изменения сигнала по преобразованию спектра данной цепью. Оба способа дают одинаковый результат, но временным способом целесообразно пользоваться при сложном спектре сигнала, а спектральным - при простом.
Спектры периодических сигналов. Обратимся к напряжению периодического сигнала произвольной формы. Мгновенное значение его U равно сумме бесконечно большого числа гармонических составляющих: постоянной составляющей U0, равной среднему значению сигнала за период Т; мгновенного значения синусоидального напряжения первой гармоники U1, у которого частота мгновенного значения синусоидального напряжения U2 второй гармоники с частотой
Для иллюстрации этой зависимости на рис 1а показано, что если в любой момент времени t сложить три синусоидальных напряжения U1,U2,U3, имеющих соответственно периоды Т1, Т2
Рис.11.1 Все гармонические составляющие образуют в совокупности спектр сигнала, изображаемый двумя диаграммами, из которых одна называется амплитудно - частотным спектром, а другая фазово-частотным. На этих диаграммах ось абсцисс образует шкалу частот f=nf1 , а на оси ординат откладываются отрезки, длина которых пропорциональна амплитуде Unm (для амплитудно-частотного спектра, рис.1б) или начальной фазы Можно исключить начальные фазы гармоник из ряда Фурье, если использовать преобразование где Теперь ряд Фурье принимает вид:
Такая запись особенно удобна в случае сигнала с чётной или нечётной временной функцией. Чётной, называется функция, которая имеет одинаковые значения f(t) для численно равных и обратных по знаку значений аргумента t, т.е. f(t)=f(-t). Этими свойствами обладают косинус (cos cos Свойствами нечётной функции обладает синус (sin Всё это приводит к выводу, что спектральная функция «чётного» сигнала содержит постоянную и только косинусные составляющие, а нечётного сигнала - постоянную и только синусные составляющие. Если сигнал выражается произвольной функцией времени, то в нём имеются оба ряда составляющих: и синусный и косинусный. Характерно, что спектр периодических сигналов не сплошной, а линейчатый, т.е. между соседними линиями спектра имеются «просветы», шириной в частоту следования сигнала Цель работы Исследование формы и спектра гармонических сигналов и периодических последовательностей импульсов. Формирование навыков спектрального анализа сигналов на ПК. Краткая характеристика исследуемых цепей и сигналов В работе используются блоки ИСТОЧНИКИ СИГНАЛОВ, сумматор (∑) и КОДЕР-1 универсального лабораторного стенда. Сменные блоки в этой работе не используются. В качестве простейших гармонических используются сигналы с частотами 1 и 2 кГц (два левых верхних гнезда стенда), а также сигналы от встроенного диапазонного генератора. Источники сигналов сложной формы, состоящих из двух гармоник (2 и 4 кГц, 2 и 6 кГц) расположены ниже - это гнезда S1, S2 и S3. Два последних сигнала отличаются фазой третьей гармоники. Все сигналы стенда (кроме встроенного ЗГ), жестко синхронизованы, так как получены от общего кварцевого генератора путем деления частоты. Это упрощает задачу получения неподвижного изображения на осциллографе. Источником импульсной последовательности является блок КОДЕР-1, позволяющий формировать произвольную пятисимвольную последовательность, повторяющуюся с периодом 17 Т, где Т=450 мкс — длительность одного символа. В качестве измерительных приборов используются: встроенный вольтметр стенда, двухлучевой осциллограф и ПК в режиме анализа спектра. Домашнее задание Изучите по литературе и конспекту лекций тему «Спектральные представления сигналов». Лабораторное задание 1. Наблюдайте осциллограммы и измерьте спектры простых гармонических сигналов. 2. Исследуйте форму и спектры сложных гармонических сигналов. 3. Исследуйте связь формы и спектра периодических последовательностей прямоугольных импульсов. Методические указания 1. Моногармонический сигнал. 1.1. Подключить осциллограф к гнезду «1 кГц» стенда. Ручку регулятора выхода сигнала поставить в среднее положение. Зафиксировать в отчете осциллограмму сигнала и измерить его период по делениям на экране с учетом цены деления (мкс/дел) переключателя развертки. 1.2. Соединить гнездо «1 кГц» с входом ПК, расположенным в нижней части стенда, правее сменного блока. Для этого надо применять специальный кабель (входит в комплект стенда) с разъемом типа «колокольчик». Процедура анализа спектра с помощью ПК описана в приложении. Зафиксировать в отчете спектр сигнала, указав условия эксперимента, амплитуды (в делениях) и точные значения частот спектральных линий (в обозначениях на стенде - округленные значения частот). 2. Сложные гармонические сигналы. 2.1. Подавая сигнал от гнезда S1 блока ИСТОЧНИКИ СИГНАЛОВ на вход осциллографа, зафиксировать форму S1(t) исследуемого сигнала и его период, а затем - на вход ПК, фиксируя амплитуды и частоты спектра сигнала. 2.2. Повторить п. 2.1 для сигналов S2 и S3. 2.3. Подать сигнал S2 на один из входов сумматора (∑) стенда, на второй его вход - сигнал от гнезда «1 кГц». Наблюдая осциллограмму сигнала на выходе сумматора, плавно увеличивать уровень сигнала «1 кГц», добиваясь заметного изменения формы суммарного сигнала. Для полученного суммарного сигнала зафиксировать осциллограмму (с указанием периода) и его спектр. 3. Бигармонический сигнал состоит из двух гармонических сигналов, частоты которых не обязательно находятся в кратных соотношениях. Такими сигналами в данном случае будут: вышеупомянутый «1 кГц» из блока ИСТОЧНИКИ СИГНАЛОВ и сигнал с частотой 1,3 кГц от встроенного ЗГ. Оба эти сигнала надо подать на входы сумматора, выставив напряжение каждого из них по 0,5 В. Для этого использовать встроенный вольтметр. Подать суммарный сигнал сначала на осциллограф, зафиксировать его форму с указанием периода суммарного сигнала, а затем на вход ПК, зафиксировав его спектр. 4. Периодическая последовательность прямоугольных импульсов формируется в блоке КОДЕР-1. «Нули» и «единицы» цифрового сигнала задаются пятью тумблерами (b1-b5) со светодиодной индикацией с надписью ПЕРЕДАНО. 4.1. Соединить выходные гнезда КОДЕРА-1 с входом осциллографа и ПК. 4.2. Набрать в КОДЕРЕ-1 комбинацию 10000 (длительность импульса Т=450 мкс, а период - 17 Т). Зафиксировать в отчете форму и спектр сигнала. 4.3. Повторить п. 4.2, набрав комбинацию 11000 (длительность импульса 2 Т, период - 17 Т). 4.4. Повторить п. 4.2 для комбинации 11110 (длительность импульса 4 Т, период- 17 Т). Отчет Отчет должен содержать для каждого пункта исследований: 1) название сигнала; 2) осциллограмму с указанием периода сигнала; 3) спектрограмму с указанием амплитуд в делениях и частот составляющих в герцах. (Желательно размещать пп. 2 и 3 на одной горизонтали.) Контрольные вопросы 1. Какова математическая связь формы периодического сигнала и его спектра? 2. Какова математическая связь формы непериодических (однократных) сигналов и их спектров? 3. Что такое прямое и обратное преобразования Фурье? 4. В каких случаях можно применить ряд Фурье для спектрального анализа? 5. Меняется ли спектр сложного сигнала при прохождении его через линейную цепь (например, ФНЧ)? 6. Меняется ли форма моногармонического сигнала при прохождении его через ФВЧ? 7. Меняется ли форма сложного сигнала при прохождении его через линейный четырехполюсник? 8. Что такое спектральная плотность амплитуд? 9. Влияет ли фазовый спектр сигнала на его форму? 10. От каких параметров сигнала зависит спектр периодической последовательности прямоугольных импульсов? 11. Как связана длительность сигнала и ширина его спектра? 12. Имеется ли связь между периодом сложного сигнала и нижней частотой его спектра?
Лабораторная работа №12 Преобразование формы и спектра сигналов безинерционным нелинейным элементом.
Теория.
Рассмотрим, как воздействует случайный процесс на нелинейную систему. В общем случае эта задача очень трудная. Дело обстоит значительно легче, когда речь идёт о безинерционных нелинейных системах, в которых выходной процесс У(t) в данный момент однозначно определяется входным процессом Х(t) в тот же момент времени. Пусть известны характеристики нелинейного устройства у =f(x) и статистические свойства входного процесса x(t). В принципе, эта задача сводится к преобразованию переменных. Рассмотрим простейший пример случайной одномерной величины. Известна плотность вероятности Р(х) случайной величины х и нужно найти плотность вероятности Р(у) случайной величины у=f(x). Предположим, что существует однозначная обратная функция x=
Поскольку плотности вероятности не могут быть отрицательными, то в формулу (1) следует подставить модуль производной. Далее можно определить среднее значение выходного процесса (постоянную составляющую).
Аналогично определяется полная мощность процесса
и функция корреляции
Энергетический спектр выходного процесса определяется с помощью преобразования Фурье от функций корреляции. Спектр процесса на выходе нелинейной системы существенно отличается от спектра на входе вследствие появления новых частотных составляющих, которые отсутствовали во входном процессе. Спектр обычно содержит низкочастотные составляющие вблизи нулевой частоты (постоянную или среднюю составляющую) и участки высокочастотных составляющих. Таким образом, при воздействии случайного процесса на нелинейную систему изменяется спектр процесса, законы распределения вероятностей и все, связанные с ними, параметры процесса. В реальных схемах усилителей при работе на нелинейном участке характеристики усилительного элемента степень искажения спектра входного сигнала на выходе усилителя характеризуется нелинейными искажениями. Основным признаком наличия нелинейных искажений в усиленном сигнале является появление в его спектре новых гармонических составляющих. Нелинейность усилителя оценивается коэффициентом гармоник (нелинейных искажений), равным отношению действующего значения появившихся в выходной цепи гармоник тока (или напряжения) к току (или напряжению) основной частоты. При этом полагают, что на вход усилителя включен источник синусоидальной ЭДС, а нагрузка усилителя представляет собой активное сопротивление, не зависящее от частоты.
где, I1,I2,I3 и т.д.- действующие или амплитудные значения первой, второй, третьей и т.д.гармоник тока на выходе; U1,U2,U3 и т.д.- действующие или амплитудные значения первой, второй, третьей и т.д. гармоник напряжения на выходе. Любое изменение спектра сигнала неизбежно приводит к изменению его формы. Объясняется это тем, что спектральный состав сигнала описывается тригонометрическим рядом Фурье, который в общем случае имеет вид:
где, U0- постоянная составляющая сигнала;
Цель работы Изучение формы и спектра сигналов на выходе резистивной цепи, содержащей нелинейный безинерционным элемент при моно- и бигармоническом воздействии. Схема работы и измерительная аппаратура В данной работе используется универсальный лабораторный стенд со сменным блоком ПРЕОБРАЗОВАНИЯ СИГНАЛОВ В НЕЛИНЕЙНОЙ ЦЕПИ. Принципиальная схема исследуемой цепи (рис. 12.1) содержит резистивный усилительный каскад на полевом транзисторе. Для формирования этой схемы достаточно переключатель НАГРУЗКА (RV LC) установить в положение «R»; состояние остальных переключателей макета безразлично (колебательный контур и связанные с ним цепи в данной работе не используются).
Рис. 12.1. Схема исследуемой цепи Источниками входных сигналов служат внутренние генераторы, гнезда и регуляторы выходного напряжения которых расположены в левой части стенда (в блоке ИСТОЧНИКИ СИГНАЛОВ). Там же находится встроенный диапазонный звуковой генератор. Входные сигналы, подаваемые на любые из трех входов макета (гнезда 1-3), а также напряжение смещения Есм через сумматор (∑) подаются на затвор полевого транзистора (гнездо КТ1). Сумматор выполнен на операционном усилителе; его коэффициент передачи по каждому входу равен -1. Схема сумматора исключает взаимное влияние между входами 1, 2 и 3, что позволяет измерять напряжения каждого источника, непосредственно на входе сумматора, не отключая остальные источники. Выходом макета является гнездо КТ2 в цепи стока. Напряжение смещения устанавливается движковым потенциометром в правой части стенда (ручкой Есм) и контролируется вольтметром, расположенным выше. Для измерения постоянной составляющей тока стока (Iс) там же расположен микроамперметр. Для включения прибора в цепь стока следует нажать кнопку «Iс» в середине сменного блока. В работе используются также встроенный вольтметр переменного напряжения, двухлучевой осциллограф и персональный компьютер (ПК), который в данной работе используется в качестве спектроанализатора. Домашнее задание Изучите по конспекту лекций и литературе теорию аппроксимации характеристик нелинейных резистивных элементов и теорию спектрального анализа. Лабораторное задание 1. Снимите и постройте вольт- амперную характеристику нелинейного элемента. 2. Исследуйте преобразование формы и спектра моногармонического сигнала на квадратичном участке вольт- амперной характеристики нелинейного элемента. 3. Исследуйте преобразование формы и спектра бигармонического сигнала на квадратичном участке вольт- амперной характеристики нелинейного элемента. 4. Выполните исследования по пп. 2 и 3 для кусочно-параболического участка характеристики. Методические указания 1. Снятие вольт- амперной (сток- затворной) характеристики полевого транзистора ic=f(ECM) производится путем последовательной установки
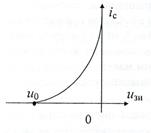
Рис. 12.2. Сток- затворная характеристика полевого транзистора
ряда напряжений смещения (см. табл. 12.1),Iс измеряя для каждого из них значения тока стока Iс. Для последнего необходимо нажать кнопку «Iс» и снять отсчет со встроенного миллиамперметра. При этом следует учесть, что полное отклонение стрелки этого прибора -5,0 мА, оно не зависит от положения переключателя пределов измерений. Во избежание ошибок при снятии вольт- амперной характеристики следует отключать все провода от входов сумматора заполнения таблицы построить график Iс(Eсм), подобный рис.12.2.
Таблица 12.1 Сток - затворная характеристика полевого транзистора
2. Моногармоническое воздействие изи = Есм + Umcos2nf1t. На построенной вольт- амперной характеристике (ВАХ) определить границы квадратичного участка (u0< Есм <0). 2.1. Преобразование на квадратичном участке ВАХ. 2.1.1. Положение рабочей точки выбирается на середине квадратичного участка ВАХ, т.е. ECM1 =u0/2, где u0 — напряжение отсечки (рис. 12.3). Установить полученное значение Есм1 потенциометром Есм и занести его в табл. 12.2.
Таблица 12.2 Спектр тока стока
2.1.2. Амплитуда входного сигнала Um1 должна быть такой, чтобы сигнал занимал весь квадратичный участок ВАХ (от нуля до отсечки), т.е
Рис.12.3 Выбор напряжения рис.12.4 Выбор амплитуды сигнала. смещения и амплитуды сигнала.
Ввиду того, что измерительные приборы имеют градуировку в действующих (U), а не амплитудных (Um) значениях, следует установить на входе макета (гнезда Вх 1, Вх 2 или Вх 3) такое напряжение от источника «1 кГц» (левое верхнее гнездо стенда), чтобы подключенный к входу вольтметр показывал U1=Um1 / 2.1.3. Временные диаграммы и спектры наблюдаются на входе (гнездо КТ1) и выходе (гнездо КТ2) преобразователя. Они зарисовываются друг под другом с сохранением соответствия, как по оси времени, так и по оси частот. Для анализа спектра на ПК соответствующее гнездо стенда соединить специальным проводом с входом «А» ПК, расположенным внизу стенда, левее встроенного вольтметра. (Для работы на ПК в режиме спектроанализатора следует изучить соответствующий раздел приложения.) На приводимых спектрограммах обязательно указывать частоты в герцах и амплитуды спектральных составляющих в делениях. Эти же данные внести в табл. 12.2. 2.2. Преобразование на кусочно-параболическом участке ВАХ. 2.2.1. Установить ЕСM2=U0 2.2.2. Установить амплитуду входного сигнала 2.2.3. Повторить п. 2.1.3 для ЕCM2 и Um2, заполнив табл. 12.3, подобную табл. 12.2. 3. Бигармоническое воздействие Uзн= ECM + U 1mcos2πf1t+ U2mcos2πf2t. В качестве второго гармонического сигнала с частотой f2= 1,3 кГц используется диапазонный звуковой генератор в блоке ИСТОЧНИКИ. На один из входов сумматора подать прежний сигнал f1=1 кГц, на любой другой - f 2=1,3 кГц. 3.1. Преобразование на квадратичном участке ВАХ. 3.1.1. Установить смещение Есm= Еcm1= u0/2 (рабочая точка на середине квадратичного участка ВАХ). 3.1.2. Установить одинаковые амплитуды сигналов от разных источников на обоих входах сумматора U1m=U2m= 3.1.3. Повторить п. 2.1.3 для новых параметров сигналов, заполнив соответствующую таблицу. 3.1.4. Повторить п. 2.1.3, предварительно уменьшив вдвое амплитуду одного из сигналов. 3.2. Преобразование на кусочно-параболическом участке ВАХ. 3.2.1. Установить Есм = ЕCM2=u0. 3.2.2. Установить амплитуды сигналов U1m=U2m= 3.2.3. Повторить п. 2.1.3 для новых параметров сигналов. Отчет Отчет должен содержать: 1) принципиальную схему исследования; 2) сток- затворную характеристику исследованной нелинейной цепи; 3) аппроксимацию ВАХ для работы на квадратичном (параболическом), кусочно-линейном и кусочно-параболическом участках; 4) теоретический расчет спектра для данных, использованных в эксперименте (по указанию преподавателя); 5) осциллограммы и спектры исследованных процессов. Контрольные вопросы
1. Каковы характерные особенности спектров тока, протекающего через нелинейный безынерционный элемент при моно- и бигармоническом воздействиях? 2. Что называется порядком комбинационного колебания? Поясните примером. 3. Какова связь между наивысшим порядком комбинационного колебания и степенью полинома, аппроксимирующего характеристику нелинейного элемента? 4. Перечислите наиболее часто применяемые методы спектрального анализа колебаний на выходе безынерционных нелинейных преобразователей. Укажите, при каких видах аппроксимации целесообразно применять каждый из них. 5. Что называется углом отсечки, как определить его по осциллограмме сигнала и как выразить аналитически? 6. Характеристика нелинейного элемента аппроксимирована ломаной линией. Входное воздействие представляет собой сигнал вида U=ECM+UmCOS 7. Поясните, как работает преобразователь, принципиальная схема которого приведена на рис. 12.1. 8. Как практически изменить положение рабочей точки на сток- затворной характеристике полевого транзистора? 9. Перечислите все составляющие спектра тока, если на вход нелинейного элемента с параболической (квадратичной) ВАХ подать гармонические сигналы с частотами 5 и 6 кГц. 10. То же для случая аппроксимации ВАХ степенным полиномом третьей степени. 11. Как изменится спектральный состав тока, если амплитуду входного напряжения уменьшить в 10 раз? Лабораторная работа № 13 ЦИФРОВАЯ СИСТЕМА СВЯЗИ Цель работы Знакомство с основными функциональными узлами цифровой системы связи для передачи как дискретных, так и аналоговых сигналов. Преобразование сигналов в отдельных блоках системы связи с разными видами модуляции и кодирования. Демонстрация помехоустойчивости системы связи. Краткая характеристика исследуемых цепей и сигналов В работе используется универсальный стенд со сменным блоком «МОДУЛЯТОР-ДЕМОДУЛЯТОР». Модель системы связи представляет собой набор функциональных узлов стенда и сменного блока, соединенных внешними перемычками: КОДЕР-1, МОДУЛЯТОР, КАНАЛ СВЯЗИ, ДЕМОДУЛЯТОР, ДЕКОДЕР-1. В КОДЕРЕ-1 осуществляется ручной набор любой пятисимвольной комбинации, которая появляется на светодиодном индикаторе под надписью ПЕРЕДАНО. МОДУЛЯТОР осуществляет один из основных видов манипуляции (AM, ЧМ, ФМ и ОФМ). При установке вида модуляции «О» выход модулятора соединен с его входом. КАНАЛ СВЯЗИ представляет собой сумматор сигнала с выхода модулятора и шума, поступающего от гнезда ГШ в блоке ИСТОЧНИКИ СИГНАЛОВ. ДЕМОДУЛЯТОР преобразует манипулированный сигнал в низкочастотный цифровой сигнал; решение о том, какой символ передавался в данном тактовом интервале, принимается в компараторе решающего устройства (РУ) и запоминается в ячейке памяти до следующего решения. Тумблер ф в сменном блоке позволяет устанавливать фазы опорных колебаний или на «О» (относительно фазы принимаемого сигнала) или на тс. Для нормальной работы демодулятора ф=0. Потенциометр ручной установки порога (только для AM) во всех случаях, кроме оговоренных особо, должен быть в крайнем левом положении. При этом светодиод не горит и пороги устанавливаются автоматически. После ДЕМОДУЛЯТОРА принятая двоичная последовательность поступает на вход ДЕКОДЕРА-1 и индицируется на табло с надписью ПРИНЯТО. При приеме цифровых сигналов, набранных в КОДЕРЕ-1, ДЕКОДЕР-1 не требуется. Для передачи аналоговых сигналов через цифровую систему связи КОДЕР-1 заменяется блоком АЦП, расположенным ниже, а блок ДЕКОДЕР-1 заменяется цифроаналоговым преобразователем (ЦАП). Блоки АЦП и ЦАП стенда могут работать с различной разрядностью (3, 4, 5 и 8 разрядов). 8-разрядное преобразование происходит при отжатых кнопках переключателя разрядности. Блок АЦП имеет два входа - «открытый» (=) и «закрытый» (~) и два выхода - основной (правые гнезда) и выход дискретизированного по времени входного сигнала (нижнее гнездо). Ниже блока АЦП расположен тумблер, позволяющий изменять частоту дискретизации = 150 Гц или = 2300 Гц. Блок ЦАП расположен в правой части стенда. При непосредственном соединении АЦП и ЦАП тумблер τ должен быть установлен в положение «О», а при использовании модулятора и демодулятора - в положение «т», так как демодулятор создает задержку на один тактовый интервал (Т). Блок ЦАП имеет два выхода: на выходе 1 формируется ступенчатый сигнал, на выходе 2 — сигнал после ФНЧ. Лабораторное задание 1. Наблюдайте сигналы в разных точках системы связи при фиксированных видах модуляции. 2. Познакомьтесь с различными видами модуляции. 3. Наблюдайте прохождение сигналов через систему связи при действии помех в канале. Методические указания 1. Передача дискретных сигналов через канал без помех. 1.1. Соединить блоки: КОДЕР-1, МОДУЛЯТОР, КАНАЛ СВЯЗИ, ДЕМОДУЛЯТОР. 1.2. Установить вид модуляции AM. 1.3. Набрать тумблерами КОДЕР А-1 произвольную кодовую комбинацию. Зарисовать осциллограммы сигналов: • на выходе КОДЕРА-1; • на выходе МОДУЛЯТОРА; • на выходе ДЕМОДУЛЯТОРА. 1.4. Переключая ВИД МОДУЛЯЦИИ, зарисовать сигналы на выходе модулятора. Обратить внимание на то, как преобразуется «О» и «1» при разных видах модуляции. 2. Передача дискретных сигналов по каналу с помехами. 2.1. Подать на нижний вход КАНАЛА n(t) сигнал с выхода генератора шума ГШ (в блоке ИСТОЧНИКИ СИГНАЛОВ). 2.2. Установить вид модуляции - ФМ. 2.3. Плавно увеличивая шумовой сигнал, добиться появления редких «сбоев» на осциллограмме выходного сигнала (на выходе ДЕМОДУЛЯТОРА). Это же явление можно наблюдать на индикаторе ошибок в сменном блоке или на табло ПРИНЯТО. 2.4. Переключив вид модуляции на AM, наблюдать увеличение частоты «сбоев». Не меняя напряжение шума, провести это же наблюдение на других видах модуляции. В отчете отметить самый лучший и самый худший вид модуляции с точки зрения помехоустойчивости. 2.5. Не меняя уровень шума, зафиксируйте осциллограммы на выходе МОДУЛЯТОРА и входе ДЕМОДУЛЯТОРА при AM. 3. Передача аналоговых сигналов через канал без помех. 3.1. Заменить КОДЕР-1 блоком АЦП, на вход которого подать сигнал S4 из блока ИСТОЧНИКИ. Выход ДЕМОДУЛЯТОРА соединить с блоком ЦАП, переключатель разрядности - в положение 3. Вид модуляции - ФМ. Регулятор шума ГШ - в крайнем левом положении (шум в канале отсутствует). Тумблер частоты дискретизации - в положение fR1, a тумблер «О vt» (около блока ЦАП) - в положение «т». 3.2. Зарисовать осциллограммы сигналов в различных точках системы связи: вход АЦП, его выход*, затем выходы 1 и 2 блока ЦАП. 3.3. Переключая разрядность, наблюдать изменение точности передачи сигнала при частоте дискретизации АЦП. 4. Передача аналоговых сигналов через канал с помехами. 4.1. Подключить входы осциллографа ко входу АЦП и второму выходу ЦАП. Вид модуляции — ФМ. 4.2. Плавно увеличивая уровень шума, добиться появления редких «сбоев» в выходной осциллограмме. 4.3. Не меняя уровень шума, по минимуму ошибок в выходной осциллограмме определить вид модуляции, обеспечивающий наилучшую и наихудшую помехоустойчивость системы связи. Свои наблюдения отразить в отчете. Здесь достаточно зарисовать любой фрагмент цифрового сигнала для двух-трех отсчетов. Отчет Отчет должен содержать: 1) функциональные схемы систем связи; 2) осциллограммы по пп.1.3, 1.4, 1.5, 3.3; 3) выводы по пп. 2.4, 2.5, 3.3, 4.3. Контрольные вопросы 1. Перечислите блоки цифровой системы связи для передачи: а) дискретных сигналов; б) аналоговых сигналов. 2. Каково назначение модулятора и демодулятора в цифровой системе связи? 3. Какова причина ошибок в работе системы связи? 4. Какие блоки «ответственны» за возникновение ошибок в системе связи? 5. Какие возможности борьбы с помехами Вам известны? 6. В чем состоит идея преобразования аналогового сигнала в цифровой и наоборот?
Приложение 1
ОТЧЕТ по лабораторной работе
По дисциплине _____________________________________________________
Тема: ______________________________________________________________
___________________________________________________________________
Цель: ______________________________________________________________
___________________________________________________________________
Порядок выполнения работы: ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ Схемы:
Перечень измерительных приборов ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ ____________________________________________________________________ Таблица _____________________________________________________________
|

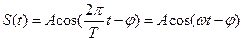 ,
, < t <+
< t <+ 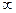 . A, Т,
. A, Т, 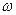 и
и  - постоянные: амплитуда, период, угловая частота, начальная фаза колебаний.
- постоянные: амплитуда, период, угловая частота, начальная фаза колебаний. равна частоте повторения сигнала
равна частоте повторения сигнала 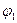 ;
;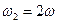 , амплитудой U2m и начальной фазой
, амплитудой U2m и начальной фазой  ,…, т.е.
,…, т.е.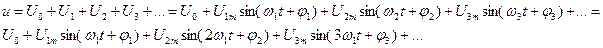
 Пользуясь знаком суммы n слагаемых
Пользуясь знаком суммы n слагаемых 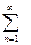 , где n любое целое число от 1 до
, где n любое целое число от 1 до 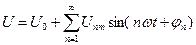
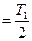 ,
, 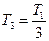 амплитуды U1m,U2m,U3m и натуральные фазы
амплитуды U1m,U2m,U3m и натуральные фазы  ,
, 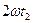 ,
, 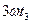 , то получится несинусоидальное напряжение U с таким же периодом Т, как у первой гармоники (Т=Т1).
, то получится несинусоидальное напряжение U с таким же периодом Т, как у первой гармоники (Т=Т1).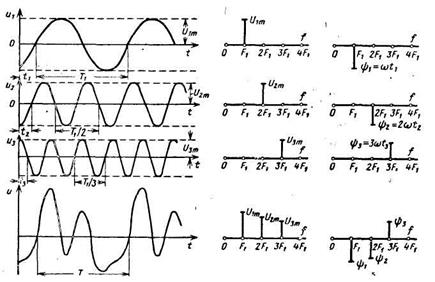
 (для фазо –частотного спектра рис.11.1,в) соответствующей n-й гармонике.
(для фазо –частотного спектра рис.11.1,в) соответствующей n-й гармонике.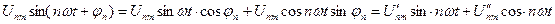 ,
, и
и 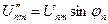 - постоянные величины, выражающие соответственно амплитуды напряжения n-гармоники для синусной и косинусной составляющих.
- постоянные величины, выражающие соответственно амплитуды напряжения n-гармоники для синусной и косинусной составляющих.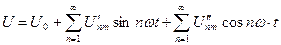
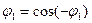 и
и 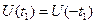 .
.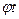 ) и всякий сигнал, симметричный относительно начала координат. Для нечётной функции характерно то, что она имеет численно равные и противоположные по знаку значения для численно равных и обратных по знаку аргументов
) и всякий сигнал, симметричный относительно начала координат. Для нечётной функции характерно то, что она имеет численно равные и противоположные по знаку значения для численно равных и обратных по знаку аргументов 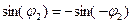 u
u 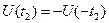
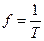 .
. … (1)
… (1)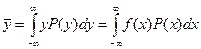 … (2)
… (2)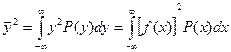 … (3)
… (3)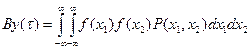 … (4)
… (4) … (5)
… (5)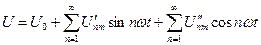 … (6)
… (6)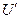 nm,
nm,  nm – амплитуды напряжений n-й гармоники для синусной и косинусной составляющих сигнала.
nm – амплитуды напряжений n-й гармоники для синусной и косинусной составляющих сигнала.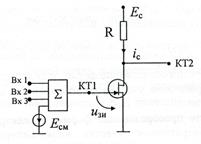
 =…B
=…B
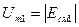 (см. рис. 12.3).
(см. рис. 12.3).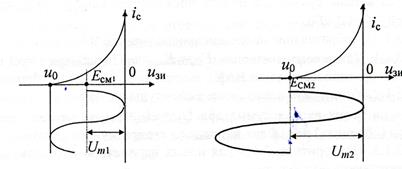
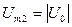 (рис.12.4). Обратите внимание на используемое здесь обозначение: Um2 означает второе значение амплитуды входного сигнала (не путать со второй гармоникой).
(рис.12.4). Обратите внимание на используемое здесь обозначение: Um2 означает второе значение амплитуды входного сигнала (не путать со второй гармоникой).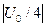 , тогда суммарный сигнал («биения») не выйдет за пределы квадратичного участка.
, тогда суммарный сигнал («биения») не выйдет за пределы квадратичного участка.