
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Статистические гипотезы. Критерии согласия.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Нулевой (основной) называют выдвинутую гипотезу Например, если нулевая гипотеза состоит в предположении, что случайная величина X распределена по закону Статистическим критерием (или просто критерием) называют некоторую случайную величину К, которая служит для проверки нулевой гипотезы. После выбора определенного критерия, например критерия Критической областью называют совокупность значений критерия, при которых нулевую гипотезу отвергают. Областью принятия гипотезы называют совокупность значений критерия, при которых гипотезу принимают. Критическими точками называют точки, отделяющие критическую область от области принятия нулевой гипотезы. Для нашего примера, при значении В случае распределения
2.6.3. Критерий согласия Одна из задач зоотехнии и ветеринарной генетики – выведение новых пород и видов с требуемыми признаками. Например, повышение иммунитета, резистентность к болезням или изменение окраски мехового покрова. На практике, при анализе результатов, очень часто оказывается, что фактические результаты в большей или меньшей степени соответствуют некоторому теоретическому закону распределения. Возникает необходимость оценить степень соответствия фактических (эмпирических) данных и теоретических (гипотетических). Для этого выдвигают нулевую гипотезу Критерием согласия называют критерий проверки гипотезы о предполагаемом законе неизвестного распределения. Имеется несколько критериев согласия: Рассмотрим применение критерия Пирсона на примере проверки гипотезы о нормальном законе распределения генеральной совокупности. С этой целью будем сравнивать эмпирические и теоретические (вычисленные в продолжении нормального распределения) частоты. Обычно между теоретическими и эмпирическими частотами есть некоторое различие. Например:
Эмпирические частоты 7 15 41 93 113 84 25 13 5 Теоретические частоты 5 13 36 89 114 91 29 14 6
Рассмотрим два случая: - расхождение теоретических и эмпирических частот случайно (незначимо), т.е. можно сделать предложение о распределении эмпирических частот по нормальному закону; - расхождение теоретических и эмпирических частот неслучайно (значимо), т.е. теоретические частоты вычислены, исходя из неверной гипотезы о нормальном распределении генеральной совокупности. С помощью критерия согласия Пирсона можно определить случайно или нет расхождение теоретических и эмпирических частот, т.е. с заданной доверительной вероятностью определить, распределена генеральная совокупность по нормальному закону или нет. Итак, пусть по выборке объема n получено эмпирическое распределение: Варианты Эмпирические частоты
Допустим, что в предположении нормального распределения вычислены теоретические частоты В качестве критерия проверки нулевой гипотезы примем случайную величину
Эта величина случайная, так как в различных опытах она принимает различные, заранее неизвестные значения. Ясно, что чем меньше различаются эмпирические Доказано, что при Обозначим значение критерия, вычисленное по данным наблюдений, через Если для вычисленного значения Замечание. При использовании критерия согласия Пирсона объем выборки должен быть не менее 30. Каждая группа должна содержать не менее 5 вариант. Если же в группах окажется менее 5 частот, их объединяют с соседними группами. В общем случае число степеней свободы для распределения хи-квадрат определяется как общее число величин, по которым вычисляют соответствующие показатели, минус число тех условий, которые связывают эти величины, т.е. уменьшают возможность вариации между ними. В простейших случаях при вычислении Пример 1. Определить степень соответствия фактического распределения групп по количеству больных туберкулезом коров с теоретически ожидаемым, которое было вычислено при рассмотрении нормального распределения. Исходные данные сведены в таблицу:
Решение. Используя критерий согласия Пирсона вычислим значение
По уровню значимости Пример 2. Теоретическое распределение по фенотипу особей, полученных во втором поколении при дигибридном скрещивании кроликов по закону Менделя составляет 9: 3: 3: 1. Требуется вычислить соответствие эмпирического распределения кроликов от скрещивания черных особей с нормальной шерстью с пуховыми животными – альбиносами. При скрещивании во втором поколении было получено 120 потомков, в том числе – 45 черных с короткой шерстью, 30 черных пуховых, 25 белых с короткой шерстью, 20 белых пуховых кроликов. Решение. Теоретически ожидаемое расщепление в потомстве должно соответствовать соотношению четырех фенотипов (9: 3: 3: 1). Рассчитаем теоретические частоты (количество голов) для каждого класса: 9+3+3+1=16, значит можно ожидать, что черных короткошерстных будет Эмпирическое (фактическое) распределение по фенотипам было следующим 45; 30; 25; 20. Сведем все эти данные в следующую таблицу:
Используя критерий согласия Пирсона вычислим значение
Число степеней свободы при дигибридном скрещивании Критерий согласия хи- квадрат Пирсона можно использовать и для сравнения друг с другом двух однородных эмпирических распределений, т.е. таких, у которых одни и те же границы классов. В качестве нулевой гипотезы
где Рассмотрим сравнение двух эмпирических распределений на следующем примере. Пример 3. Проводился промер длины яиц кукушек по двум территориальным зонам. В первой зоне была обследована выборка из 76 яиц (
При уровне значимости Решение. Так как количество классов первого ряда частот отличается от количества классов второго ряда, и к тому же количество вариант в некоторых классах мало, произведем объединение первых двух классов и последних четырех (таблица А) в результате получили 7 классов вместо 11. Преобразуем исходную таблицу, добавив к ней строки с промежуточными результатами вычислений (таблица Б). Таблица А
Таблица Б
Используя критерий (**), получим
Число степеней свободы в этом случае будет равно
Распределение Стьюдента. В биологических исследованиях нередко приходится встречаться с выборочными совокупностями, состоящими из очень ограниченного количества вариант или наблюдений. Возникает вопрос, каковы в этих случаях закономерности распределения выборочных средних арифметических. Ответ на него дал английским математик В. Госсет, который писал под псевдонимом Стьюдент. Поэтому полученное им распределение вероятностей получило название распределения Стьюдента. Пусть то случайная переменна
распределена по закону Стьюдента с n-1 степенями свободы. Здесь
Распределение Т отличается только при малом объеме выборки. Так как В общем случае случайная величина Т определяется как
где Z – нормальная случайная величина, причем M(Z)=0, Покажем, что случайная величина (*) представляет собой частный случай случайной величины Т, распределенной по закону Стьюдента. Представим выражение (*) в следующем виде:
Величина Распределение Стьюдента зависит только от числа степеней свободы Математическое ожидание М(Т) распределения Стьюдента при Для практического использования t – распределения были составлены рабочие таблицы, по которым можно определять критические значения Замечание. Следует иметь в виду, что в случае односторонней критической области значения уровня значимости
Рис. 18. Распределение Стьюдента в зависимости от числа свободы k; сравнение со стандартизованным нормальным распределением.
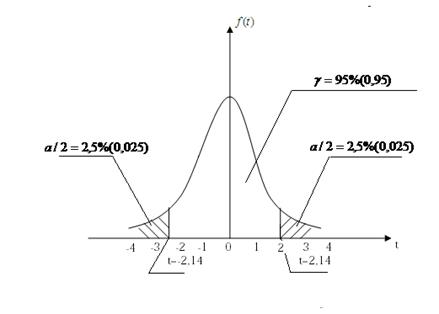
Рис. 19.95% доверительная вероятность и 5% уровень значимости для распределения Стьюдента.
Распределение Фишера. Во многих задачах математической статистики, в особенности в дисперсионном анализе, важную роль играет распределение Фишера (F-распределение), названное так по фамилии известного английского математика Р.А. Фишера (1925 г.) Если U и V независимые случайные величины, распределенные по закону
распределена по закону Фишера со степенями свободы На практике часто применяется случайная величина
Распределенная по закону Стьюдента с числом степеней свободы
Покажем, что случайная величина (**) представляет собой частный случай случайной величины (*). Перепишем (**) в виде
Случайные переменные Величина F имеет непрерывную функцию распределения и зависит только от чисел степеней свободы Наиболее часто функция F распределения табулирована для 5% (доверительная вероятность 0,95) и 1% (доверительная вероятность 0,99) уровней значимости и чисел степеней свободы
Рис. 20. Функция распределения Рис. 21. Функция распределения Фишера с односторонней Фишера с двухсторонней критической областью. критической областью.
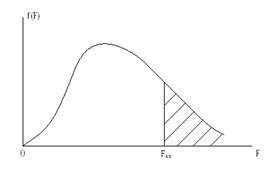
Рассмотрим подробнее построение критических областей распределения Фишера. При использовании случайной величины F в качестве критерия проверки нулевой гипотезы о равенстве генеральных дисперсий критическая область строится в зависимости от вида конкурирующей гипотезы. Первый случай: Нулевая гипотеза В этом случае строят одностороннюю, а именно правостороннюю, критическую область (рис. 20) исходя из требования, чтобы вероятность попадания величины F в эту область, в предположении справедливости нулевой гипотезы, была равна принятому уровню значимости р. Тогда правосторонняя критическая область определяется неравенством Второй случай: Нулевая гипотеза В этом случае строят двухстороннюю критическую область (рис.21) исходя из требования, чтобы вероятность попадания величины F в каждый из двух интервалов критической области, в предположении справедливости конкурирующей гипотезы, была равна Доверительные интервалы Доверительные интервалы находят по различным формулам, в зависимости от исходных данных.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-26; просмотров: 1784; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.041 с.) |

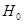 о виде неизвестного распределения, или о параметрах известных распределений. Конкурирующей (альтернативной) называют гипотезу
о виде неизвестного распределения, или о параметрах известных распределений. Конкурирующей (альтернативной) называют гипотезу 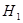 , которая противоречит нулевой.
, которая противоречит нулевой.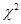 , то конкурирующая гипотеза может состоять в предположении, что случайная величина Х распределена по другому закону.
, то конкурирующая гипотеза может состоять в предположении, что случайная величина Х распределена по другому закону.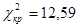 , вычисленное по выборке значение
, вычисленное по выборке значение 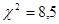 соответствует области принятия гипотезы: случайная величина распределена по закону
соответствует области принятия гипотезы: случайная величина распределена по закону 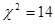 , то оно попадает в критическую область, то есть гипотеза о распределении случайной величины по закону
, то оно попадает в критическую область, то есть гипотеза о распределении случайной величины по закону 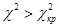 , область принятия нулевой гипотезы – неравенством
, область принятия нулевой гипотезы – неравенством 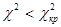 .
.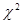 Пирсона.
Пирсона.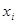
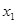
 ……
…… 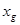
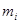
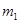
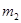 …….
……. 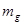
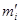 . При уровне значимости
. При уровне значимости 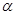 требуется проверить нулевую гипотезу
требуется проверить нулевую гипотезу 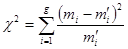 (*)
(*)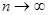 закон распределения случайной величины (*), независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения
закон распределения случайной величины (*), независимо от того, какому закону распределения подчинена генеральная совокупность, стремится к закону распределения  степенями свободы. Поэтому, случайная величина (*) обозначается через
степенями свободы. Поэтому, случайная величина (*) обозначается через 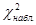 . Табулированные критические значения критерия для данного уровня значимости
. Табулированные критические значения критерия для данного уровня значимости 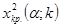 . При этом число степеней свободы определяют из равенства
. При этом число степеней свободы определяют из равенства 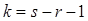 , где
, где 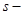 число групп (частичных интервалов) выборки или классов;
число групп (частичных интервалов) выборки или классов; 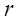 - число параметров предполагаемого распределения. У нормального распределения два параметра – математическое ожидание и среднее квадратическое отклонение. Поэтому число степеней свободы для нормального распределения находят из равенства
- число параметров предполагаемого распределения. У нормального распределения два параметра – математическое ожидание и среднее квадратическое отклонение. Поэтому число степеней свободы для нормального распределения находят из равенства 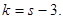
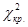
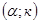 выполняется неравенство
выполняется неравенство 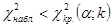 , принимается нулевая гипотеза
, принимается нулевая гипотеза 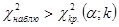 , нулевую гипотезу отвергают и принимают гипотезу, альтернативную ей (генеральная совокупность не распределена по нормальному закону).
, нулевую гипотезу отвергают и принимают гипотезу, альтернативную ей (генеральная совокупность не распределена по нормальному закону). .
. Теоретическое
Теоретическое 
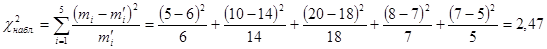
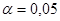 и числу степеней свободы
и числу степеней свободы 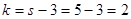 из таблицы критических точек распределения
из таблицы критических точек распределения  . Поскольку
. Поскольку 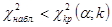 , можно сделать вывод, что различие между теоретическими и фактическими частотами носит случайный характер. Таким образом, фактическое распределение групп по количеству больных туберкулезом коров соответствует теоретически ожидаемому.
, можно сделать вывод, что различие между теоретическими и фактическими частотами носит случайный характер. Таким образом, фактическое распределение групп по количеству больных туберкулезом коров соответствует теоретически ожидаемому. ; черных пуховых -
; черных пуховых -  ; белых короткошерстных -
; белых короткошерстных - 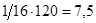 .
.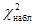 :
: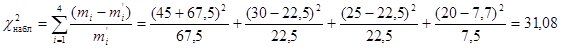
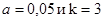 находим значение
находим значение  . Поскольку
. Поскольку 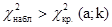 , можно сделать вывод, что различие между теоретическими и фактическими частотами является неслучайным. Следовательно, полученная группа кроликов отклоняется по распределению фенотипов от закона Менделя при дигибридном скрещивании и отражает влияние неких факторов, изменяющих тип расщепления по фенотипу у второго поколения помесей.
, можно сделать вывод, что различие между теоретическими и фактическими частотами является неслучайным. Следовательно, полученная группа кроликов отклоняется по распределению фенотипов от закона Менделя при дигибридном скрещивании и отражает влияние неких факторов, изменяющих тип расщепления по фенотипу у второго поколения помесей. (**)
(**)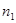 и
и 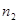 - объемы сравниваемых распределений;
- объемы сравниваемых распределений; 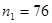 ), во второй из 54 (
), во второй из 54 (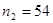 ). Получены следующие результаты:
). Получены следующие результаты: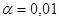 требуется проверить нулевую гипотезу, что обе выборки яиц принадлежат одной популяции кукушек.
требуется проверить нулевую гипотезу, что обе выборки яиц принадлежат одной популяции кукушек.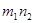

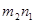
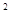
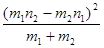
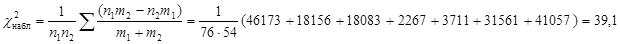
 , так как число классов равно 7, а единственным общим элементом двух рядов является одинаковое число классов. По уровню значимости
, так как число классов равно 7, а единственным общим элементом двух рядов является одинаковое число классов. По уровню значимости 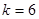 из таблицы критических точек распределения
из таблицы критических точек распределения  . Так как
. Так как 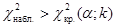 , нулевая гипотеза, что обе выборки яиц взяты из одной популяции должна быть отвергнута.
, нулевая гипотеза, что обе выборки яиц взяты из одной популяции должна быть отвергнута. - нормально распределенные независимые случайные величины с математическим ожиданием
- нормально распределенные независимые случайные величины с математическим ожиданием 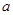 и дисперсией
и дисперсией  . Если
. Если  и
и 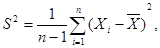
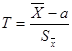 (*)
(*)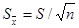 - оценка среднего квадратического отклонения выборочной средней. Легко видеть, что переменная Т принципиально сходна с формулой нормированного отклонения выборочной средней от генеральной при нормальном распределении для больших выборок:
- оценка среднего квадратического отклонения выборочной средней. Легко видеть, что переменная Т принципиально сходна с формулой нормированного отклонения выборочной средней от генеральной при нормальном распределении для больших выборок: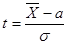
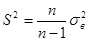 , с увеличением числа n получаем равенство
, с увеличением числа n получаем равенство 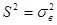 и разница между распределением Т и нормальным практически исчезает.
и разница между распределением Т и нормальным практически исчезает.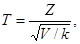 (**)
(**) а V – независимая от Z величина, которая распределена по закону
а V – независимая от Z величина, которая распределена по закону 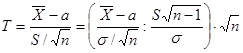
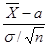 имеет нормальное распределение, величина
имеет нормальное распределение, величина 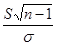 распределена по закону
распределена по закону 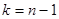 степенями свободы. Таким образом, мы получили случайную величину (**).
степенями свободы. Таким образом, мы получили случайную величину (**). практически не отличается от него. На рис. 18 на фоне нормального распределения показаны кривые распределения Стьюдента при различных степенях свободы.
практически не отличается от него. На рис. 18 на фоне нормального распределения показаны кривые распределения Стьюдента при различных степенях свободы.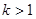 равно 0, дисперсия
равно 0, дисперсия 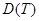 при
при  равна
равна 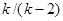 .
. , соответствующие данной доверительной вероятности
, соответствующие данной доверительной вероятности 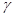 и числу степеней свободы
и числу степеней свободы 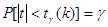 (вероятность того, что случайная величина t по абсолютной величине меньше критического значения
(вероятность того, что случайная величина t по абсолютной величине меньше критического значения 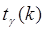 равна доверительной вероятности
равна доверительной вероятности 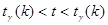 . Так, например, если выборка включает 15 наблюдений (число степеней свободы k=n-1=14) и по условиям опыта требуется доверительная вероятность 0,95 (уровень значимости 0,05), то величина t должна быть менее 2,14 и более -2,14. На рис. 19 показан графический смысл этих величин.
. Так, например, если выборка включает 15 наблюдений (число степеней свободы k=n-1=14) и по условиям опыта требуется доверительная вероятность 0,95 (уровень значимости 0,05), то величина t должна быть менее 2,14 и более -2,14. На рис. 19 показан графический смысл этих величин.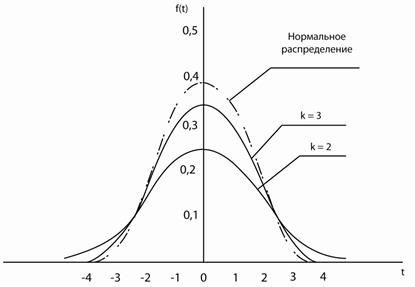
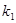 и
и  , то величина
, то величина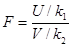 (*)
(*)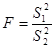
 ), (**)
), (**) (для большей дисперсии) и
(для большей дисперсии) и  (для меньшей дисперсии). Здесь
(для меньшей дисперсии). Здесь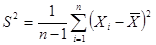 .
.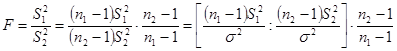 .
.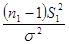 и
и 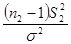 распределены по закону
распределены по закону 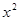 со степенями свободы
со степенями свободы 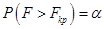 . В случае двухсторонней критической области критическим значением
. В случае двухсторонней критической области критическим значением 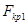 и
и 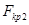 соответствует вероятности
соответствует вероятности  и
и 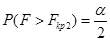 . На практике при двухсторонней критической области ограничиваются определением величины
. На практике при двухсторонней критической области ограничиваются определением величины 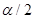 .
.
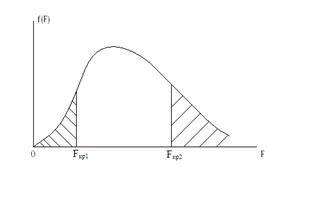
 . Конкурирующая гипотеза
. Конкурирующая гипотеза 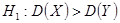 .
. . Значение
. Значение 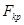 находят по заданному уровню значимости
находят по заданному уровню значимости 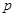 при степенях свободы
при степенях свободы  . Конкурирующая гипотеза
. Конкурирующая гипотеза 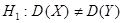 .
.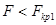 ,
,  ; область принятия нулевой гипотезы:
; область принятия нулевой гипотезы: 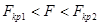 .
.


