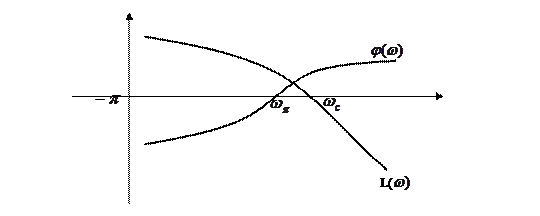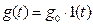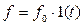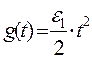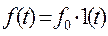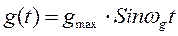Логарифмический критерий устойчивости

Широкое распространение критерий Найквиста получил при суждении об устойчивости по логарифмическим частотным характеристикам. Возможность такого суждения вытекает из того, что АФХ разомкнутой системы

W(j )=|W(j )|·e^{j arg W(j )}

Полностью определяется парой характеристик

L()=20 lg|W(j )| и j()=arg W(j )

Точками пересечения годографа W(j ) с отрезком отрицательной вещественной оси (-¥,-1) соответствуют точки для которых.

 

Точки ЛФЧХ , для которых L(w)>0 и в которых она пересекает при увеличении w прямые -p,-3p,… снизу вверх условимся называть отрицательными переходами П_-, а сверху вниз – положительными переходами П₊.

Тогда критерий устойчивости может быть сформулирован следующим образом. САР устойчива, если разность между положительными и отрицательными переходами ЛАЧХ равна l/2, где l – число корней характеристического уравнений разомкнутой системы, лежащих в правой полуплоскости. П₊-П_-=l/2

Для частного случая, когда l=0 (разомкнутая система устойчивая или нейтральна), получается, что система устойчива, если разность между

П₊ - П- = 0.

 

Если пересечение j(w) с осью -p происходит только один раз

П₊-П_- = -1¹0; l=0 – система неустойчивая

w_с>w_п

П₊-П_-=0-0-0; l=0 – замкнутая система устойчивая

w_с<w_п

 

Замкнутая система будет устойчивая, когда L(w)=0 достигается раньше, чем j(w)= -p. Если w _с= w_п замкнутая система находится колебательной границе устойчивости.

 

Критерии качества

 

Устойчивость САР – необходимое, но далеко не достаточное условие её практической пригодности. Качество САР определяется, прежде всего, точностью управления. А оно, в конечном счёте, зависит от мгновенных величин ошибки e(t),

e(t)=g(t)-x(t), (1)

Ошибка в свою очередь определяется характером изменения входного и возмущающего воздействий. Обычно они представляют собой случайные функции времени, которые могут быть заданы лишь вероятностными характеристиками. В этом случае применяются вероятностные оценки ошибки e(t).

Однако вероятностный подход к проблеме качества не является единственным. В ТАР широко используются методы, позволяющие оценивать качество системы по их поведению в типовых режимах, когда случайные по своей природе воздействия апроксимируются заданными (типовыми) функциями времени. Оценка ведётся по так называемым критериям или показателям качества.

В общем случае критерии качества h_i представляют собой функционалы от разности (1), т.е. функционалы от ошибки

h_i=F_i[g(t)-x(t)]=F_i[e(t)], i=1,m

Все критерии качества можно условно разделить на 4 группы: критерии точности, запаса устойчивости, быстродействия и комбинированные.

Критерии точности используют для оценки величины ошибок, возникающих в различных типовых установившихся режимах и в случаях, когда g(t) и f(t) представляют собой плавные, медленно меняющиеся функции времени. К наиболее распространённым типовым режимам относятся такие, при которых

 

для следящих систем важны режимы, когда

где W₁ – const; e₁- const, при

 

 

Критерием точности служит значение ошибки в установившемся режиме e_уст.

Критерий запаса устойчивости определяет отдалённость системы от границы устойчивости. Для оценки качества системы по этому критерию используют два полхода.

Один подход основан на рассмотрении переходных процессов системы (переходной или весовой функции), расположения полюсов и нулей передаточной функции замкнутой системы и т.д. При этом показателями запаса устойчивости служат величина перерегулирования, колебательность и затухание переходного процесса.

Второй подход основан на изучении частотных и резонансных свойств системы, а также поведения её частотных характеристик. В качестве критериев запаса устойчивости используют запас устойчивости по амплитуде и фазе, показатели колебательности и др.

Оба подхода (временной и частотной) используются при оценке быстродействия системы. Критерием быстродействия в первом случае может служить время затухания переходного процесса системы, а во втором – полоса пропускания АЧХ замкнутой системы.

Иногда временные критерии качества называют прямыми в том смысле, что при их помощи оценивается непосредственно процесс управления. Частотные критерии называют косвенными – оценка по отображению процесса в частотной области. Обычно вычисления, проводимые в частотной области, проще, чем во временной. Поэтому частотные критерии являются эффективным средством оценки качества процессов управления.

К комбинированным критериям качества относятся обобщённые критерии, характеризующие одновременно, точность, запас устойчивости и быстродействие (интегральные оценки и т.д.).