
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Спектральные характеристики некоторых функцийСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
1.Единичная ступенчатая функция. Дельта – функция. Функция 1(t) вида
называется единичной ступенчатой функцией. Из (1) следует, 1(t) при t=0 имеет разрыв неопределенности первого рода, причем значение функции в точке разрыва не определено. Однако 1(t) при t=0 приписывают вполне определённые значения. Наиболее часто встречаются функции следующего вида:
Выбор того или иного значения единичной функции t=0 связан особенностями решаемой задачи. Например, первое представление удобно в том случае, когда рассматривают функцию 1(t) как предел при λ→∞ последовательности непрерывных функций: f(t,λ)=1/2+(1/π)arctg λt (3), где λ – параметр и
Последовательность непрерывных функций
при λ→ ∞ также имеет своим пределом первое представление 1(t). Если
К категории особых функций относится дельта – функция Дирака, называется также импульсной функцией, первого порядка. Дельта функция определяется равенством:
Условия (6) и(7) оказываются несовместимыми, если рассматривать их с позиций классического матанализа, и поэтому дельта – функция не является функцией в обычном смысле. Однако в классе обобщенных функций она занимает равноправное место. Дельта–функция обычно рассматривается как предел последовательностей дельта - образных гладких (имеющих производные любого порядка) функций являющихся производными по t от (3). Например:
является дельта – образной последовательностью, т.к.
В самом деле, при t≠0
при t=0
При таком определении дельта – функция является четной. Дельта – функция может апроксимироваться и разрывными функциями. Например, последовательность функций
Смещенная единичная ступенчатая функция и дельта–функции определяются равенствами:
Рассмотрим важное свойство дельта – функции. Пусть f(t) непрерывна и ограниченна в интервале [-∞;∞]. Тогда справедливо равенство:
Это соотношение определяет так называемое “фильтрующее” или “выхватывающее” свойство дельта – функции. Определим теперь спектральные характеристики 1(t). Единичная ступенчатая функция не удовлетворяет условию абсолютной интегрируемости, и поэтому преобразование Фурье для такой функции не существует. Однако, используя понятие дельта–функции, можно построить спектральную характеристику и для неё. Покажем, что её спектральная характеристика определяется равенством:
Подставляя F(jω) в формулу обратного преобразования Фурье и, учитывая фильтрующее свойство дельта–функции, получим
Учитывая Лемму Жордана и основанные на ней способы вычисления несобственных интегралов, найдём
Следовательно:
Таким образом, обратное преобразование Фурье функции F(jω) приводит к 1(t), и поэтому правая часть равенства (10) является её спектральной характеристикой. Определим спектральную характеристику дельта–функции (6). Применяя
Спектральная характеристика смещенной дельта-функции будет
Из (11) и (12) следует, что модуль спектральной характеристики дельта-функции │F(jω) │ равен единице.
Отсюда следует, что амплитуды гармоник представления δ - функции в виде интеграла Фурье равны на всем диапазоне частот от -∞ до ∞. Найдем спектральную характеристику суммы двух дельта-функций
2. Гармонические колебания. Пусть задана косинусоидная функция
f(t) = А1 Cos ω1 t c амплитудой А1 и частотой ω1. Амплитудный спектр этой функции состоит из двух отрезков высотой А1 при частотах ω= ± ω1; для других значений частоты ω значения амплитудного спектра равны нулю.
Косинусоида не удовлетворяет условию абсолютной интегрируемости на интервале (-∞;∞) поэтому преобразование Фурье непосредственно не может быть использовано для определения спектральной характеристики (13). Покажем, что
Для этого используем обратное преобразование Фурье
Подставляя в эту формулу выражение (14) получим
Здесь использовано фильтрующее свойство дельта-функции, причем точка ω=ω1, расположена внутри интервала (0, ∞), а δ(ω+ω1) = 0 при ω>0. Следовательно, с учетом формулы Эйлера
т.е.
Пусть теперь задана периодическая функция
Ее спектральная характеристика.
Если
её модуль
|
|||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 638; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.209.66 (0.008 с.) |





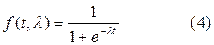
 , то предел этой последовательности
, то предел этой последовательности
 , причем
, причем
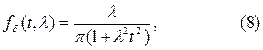


 , причем
, причем
 , характеризующих импульсы высотой 1/a и длительностью a, при a→0, сходятся к дельта функции, т.е.
, характеризующих импульсы высотой 1/a и длительностью a, при a→0, сходятся к дельта функции, т.е.






 , получим учитывая фильтрующее свойство:
, получим учитывая фильтрующее свойство: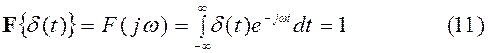








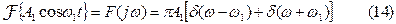
 .
.

 даём косинусоиду, следовательно
даём косинусоиду, следовательно


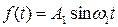
 ,
,





