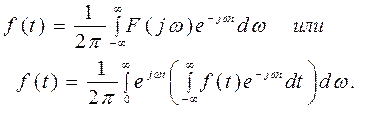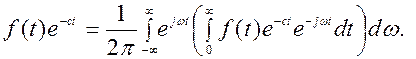Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предельный переход от ряда Фурье к интегралу ФурьеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Для разложения функции f(t) в ряд Фурье на всей оси 0 t необходимо, чтобы эта функция была периодической. При представлении функции заданной в интервале (-π/2; π/2), в виде ряда Фурье в этом интервале, функция периодически продолжается с периодом Т за пределы этого интервала. В этом случае получающаяся периодическая функция представляется в виде бесконечной суммы гармоник. Установим, что будет с разложением, если Т→ ∞. Пусть дана периодическая функция f(t), допускающая в интервале (-Т/2; Т/2) разложение в ряд Фурье т.е.
или в другой форме
где При Т→ ∞ частота первой гармоники разложения f(t) в ряд Фурье: ∆ω=2π/Т → 0. Однако величина ∆ω является приращением частоты при переходе от одной частоты к соседней. При Т→ ∞ приращение частоты становится величиной бесконечно малой, т.е. ∆ω → dω. Обозначим через ω часиоту k –ой гармоники, т.е. положим ω=k∆ω. Под знаком суммы в правой части (2) величина ω принимает дискретные значения. Если Т→ ∞ то ω становится непрерывной величиной. В этом случае
или F(jω) = U(ω)-jV(ω), где функция U(ω) – четная, а V(ω) – нечетная относительно ω. Функцию F(jω) можно записать в виде:
где
Сравним преобразование Фурье F(jω) c относительной комплексной амплитудой k – ой гармоники F(jk∆ω).
В пределе при Т → ∞ (т.е. при ∆ω → 0) правая часть этого равенства совпадает с правой частью равенства (4), т.е. учитывая, что
где Функция F(jk∆ω) даёт при фиксированном k значение относительной амплитуды k- й гармоники разложения периодической функции в ряд Фурье. Если k=0,1,2…,то F(jk∆ω) принимает значения F (jo), F(j∆ω), F(j2∆ω). Функция F(jω) характеризует закон изменения относительных комплексных амплитуд разложения непериодической функции на сумму гармоник, так как частота ω принимает непрерывный ряд значений, то график F(jω) состоит не из отдельных (дискретных) точек, а является непрерывной кривой. Интеграл Фурье дает разложение, представляющее собой сумму бесконечно большого числа гармоник, амплитуды которых бесконечно малы, а частоты смежных гармоник бесконечно близки. Комплексная бесконечно малая амплитуда каждой гармоники, как следует из (5) будет
Амплитуды каждой гармоники в разложении с помощью интеграла Фурье бесконечно малы, поэтому изобразить их на графике не представляется возможным. Поэтому для того, чтобы использовать спектральное представление и для анализа непрерывных процессов по оси ординат откладывают не амплитуду гармоники А, а значение относительной амплитуды. Для периодической функции f(t) получится график
график, характеризующий среднее значение амплитуды, приходящейся на единицу длины интервала частот. В пределе, при Т→ ∞ функция F(j∆ω) превращается в F (jω) непериодической функции f(t), которая с точностью до постоянного множителя π представляет собой отношение бесконечно малого приращения амплитуды, имеющей место при бесконечно малом приращении частоты к указанному приращению частоты
Аргумент спектральной характеристики argF(jω) = φ(ω) характеризует начальную фазу гармоник разложения непериодической функции f(t), а функция Пример. Определить частотные свойства одиночного импульса высотой А и длительностью τ.
Периодически продолжаем функцию с периодом Т и находим коэффициенты ak и bk, функция четная bk=0.
Амплитудно-частотный спектр Ak =│ak│ будет иметь вид:
Графически спектр одиночного импульса изобразить нельзя. Построим график функции │F(jk∆ω) │, т.к.
Первое значение:
При k=0,1,2 … F(jk∆ω) принимает дискретный ряд значений. Через концы отрезков проходит огибающая │F(jω) │, величина площадей заштрихованных прямоугольников с точностью до множителя π равна ak. Нетрудно видеть, что в отличие от огибающей для частотного спектра ak кривая │F(jω) │не зависит от уменьшения (увеличения) частотного интервала ∆ω, происходящего при увеличении (уменьшении) периода Т последовательности импульсов. При Т → ∞ интервал станет бесконечно малым, однако относительные амплитуды остаются неизменными. В данном примере
ПРЕОБРАЗОВАНИЕ ФУРЬЕ Прямое и обратное преобразование Фурье Совокупность операций, позволяющих по заданной функции f(t) находить соответствующую ей спектральную характеристику F(iω) называется преобразованием Фурье:
Символически формулу (1)будем записывать в виде
Интеграл в правой части (1) как и ранее понимается в смысле главного значения, т.е.
Равенство (1) устанавливает связь между функцией f(t), аргументом которой служит t, и ей соответствующей комплексной функцией F(iω), имеющей в качестве аргумента частоту ω. Формула интеграла Фурье
позволяет от известной функции F(iω) определить соответствующую ей функцию f(t). На этом основании формулу (3) называют обратным преобразованием Фурье. Символически будем записывать
В ряде задач автоматического регулирования функция f(t) характеризует процесс, имеющий место лишь начиная с некоторого момента времени t, который можно принять за нулевой. В этом случае f(t) ≡ 0 при t < 0 (1) принимает вид
Преобразование (5) называется прямым односторонним преобразованием Фурье. Обратное преобразование Фурье, соответствующее прямому одностороннему преобразованию, остается двусторонним по переменной ω и дается равенством
При t= 0, значение правой части (6) равно при t < 0, f(t) ≡ 0
СВЯЗЬ ПРЕОБРАЗОВАНИЙ ФУРЬЕ И ЛАПЛАСА Формула
прямого преобразования Лапласа может рассматриваться как результат определенным образом построенного обобщения одностороннего преобразования Фурье. Пусть, например, f(t) удовлетворяет условиям Дирихле в интервале 0 ≤ t < ∞, причем f(t) ≡ 0 при t< 0. Как известно, преобразование Фурье может быть применено к функциям f(t), для которых интеграл Для того чтобы иметь возможность подобную функцию f(t) преобразовать по Фурье, предварительно ее надо умножить на e-ct где вещественное число С>C0 выбрано таким образом, чтобы интеграл Значение С0 для каждой функции f(t) является вполне определенным. Используя формулу прямого одностороннего преобразования Фурье, будем преобразовывать по Фурье не f(t), а f(t)e-ct, удовлетворяющую условиям применения этого преобразования.
Введя новую комплексную переменную S=c+jω, получим Это выражение представляет собой формулу прямого преобразования Лапласа. Таким образом, преобразование Лапласа является результатом распространения преобразования Фурье на функции, которые, удовлетворяя условиям Дирехле в интервале 0<t< ∞, не удовлетворяют в этом интервале условию абсолютной интегрируемости. Если F(jω) спектральная х – тика f(t), то функция F(S) комплексной переменой S является спектральной характеристикой затухающей функции времени f(t)e-ct. Рассмотрим формулу обратного преобразования Фурье:
Заменим в правой и левой частях этого равенства f(t) на f(t)e-ct, получим:
Учитывая, что S=e + jω, dω=dS/j, найдём
Это равенство является формулой обратного преобразования Лапласа, т.е. обратное преобразование Лапласа может рассматриваться как развитие обратного преобразования Фурье. Ранее отмечалось, что представление функции в виде интеграла Фурье соответствует представлению функции в виде суммы бесконечно большого числа гармоник с бесконечно малыми амплитудами, причем частоты гармоник отличаются друг от друга бесконечно мало. Аналогично этому представлению f(t) в виде (*) соответствует представлению этой функции в виде бесконечно большого числа бесконечно малых составляющих, являющихся колебаниями с бесконечно малыми амплитудами, затухающих по экспоненциальному закону. Свойства преобразования Фурье аналогичны свойствам преобразования Лапласа.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-21; просмотров: 518; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.99.80 (0.01 с.) |

 ∆ω=2π/T
∆ω=2π/T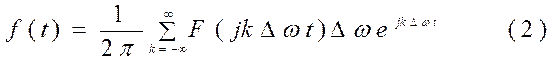
 - относительная комплексная амплитуда.
- относительная комплексная амплитуда.
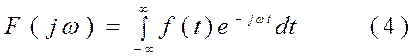
 Функция F(jω) называется преобразованием Фурье функции f(t).Эта функция характеризует спектральный состав функции f(t) и может быть названа также спектральной характеристикой f(t).Используя формулу Эйлера (3) можно представить в виде:
Функция F(jω) называется преобразованием Фурье функции f(t).Эта функция характеризует спектральный состав функции f(t) и может быть названа также спектральной характеристикой f(t).Используя формулу Эйлера (3) можно представить в виде:


 - модуль преобразования Фурье, четная функция.
- модуль преобразования Фурье, четная функция. - аргумент, нечетная функция.
- аргумент, нечетная функция.
 , найдем
, найдем


 т.е.
т.е.
 является относительной амплитудой этих гармоник.
является относительной амплитудой этих гармоник.









 является действительной. В общем случае она может быть и комплексной.
является действительной. В общем случае она может быть и комплексной.
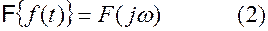



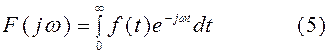
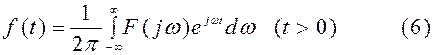
 ;
;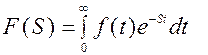
 существует (условие абсолютной интегрируемости). Этому условию не удовлетворяют многие функции, используемые при анализе процессов в автоматических системах, например 1(t), Asin(ω t), Acos(ω t), eαt при α >0, t и др.
существует (условие абсолютной интегрируемости). Этому условию не удовлетворяют многие функции, используемые при анализе процессов в автоматических системах, например 1(t), Asin(ω t), Acos(ω t), eαt при α >0, t и др. был бы сходящимся.
был бы сходящимся.
 .
.