
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Использование методов численного интегрирования при разложении функции в ряд ФурьеСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Разложение функции в ряд Фурье, или гармонический анализ, оказывается нужным во многих чисто практических вопросах машиноведения, электротехники и пр. Но в этих случаях очень редко приходится непосредственно пользоваться формулами Эйлера-Фурье:
для вычисления коэффициентов разложения. Дело в том, что функции, которые нужно подвергнуть гармоническому анализу, обыкновенно задаются таблицей своих значений или графиком. Таким образом, аналитического выражения функции в нашем распоряжении нет; иногда к самому гармоническому анализу прибегают именно для того, чтобы таким путем получить хотя бы приближенное аналитическое выражение для функции. В этих условиях для вычисления коэффициентов Фурье нужно обратиться к приближенным методам. Разумеется, на практике приходится пользоваться лишь немногими первыми членами тригонометрического разложения. Коэффициенты ряда Фурье в большинстве случаев убывают, а с ними быстро падает и влияние далеких гармоник. Обычно дается (или снимается с графика) ряд равноотстоящих ординат, т.е. ряд значений функции Можно сделать вывод, что ряды Фурье широко применяются в инженерно-технических расчетах. Они часто встречаются при рассмотрении ряда задач измерительной техники, особенно при исследовании колебательных процессов в измерительных системах, а также при анализе результатов измерений нестационарных параметров. Пример буден приведен при решении нулевого варианта контрольной работы. Вопросы для самопроверки 1. Запишите формулу средних прямоугольников для вычисления определенного интеграла Примерный вариант и образец выполнения Контрольной работы по теме «Ряды Фурье» Задача 1. Разложить в ряд Фурье функцию Решение. Построим график функции
Эта функция f(x) имеет период По формуле (2) найдем коэффициент
Найдем
По формуле (4)
Подставляя коэффициенты в формулу (1), получаем Это равенство справедливо во всех точках, кроме точек разрыва. В каждой точке разрыва сумма ряда равна среднему арифметическому ее предельных значений изнутри отрезка, то есть в точке x =0.
Ответ. Построим график S4(x)
Задача 2. Разложить в ряд Фурье функцию Решение. Построим график
1. Продолжая эту функцию на промежуток
Ряд для такого разложения Построим S5(x)
2. Продолжая эту функцию на промежуток
Эта функция f(x) имеет период
Это равенство справедливо во всех точках числовой прямой. Построим график S4(x)
Задача3. Разложить в ряд Фурье периодическую функцию Решение. Построим эскиз графика функции Проверив выполнение условий Дирихле для функции, переходим к вычислению коэффициентов Фурье. Заданная функция общего вида с периодом Т=6, l=3, поэтому в разложении ее ряд Фурье имеет вид:
Подставляя коэффициенты в формулу ряда, получаем Построим график S5 (x)
Можно совместить оба графика на одном чертеже
Отметим близость этих графиков. Задача4. Разложить в ряд Фурье функцию Решение. Будем считать функцию периодической с периодом T =3-1=2, l =1 т.е.
Ряд Фурье для этой функции будет иметь следующий вид: Проверив выполнение условий Дирихле для функции, переходим к вычислению коэффициентов Фурье.
Построим график S5 (x)
Задача 5. Разложить в комплексный ряд Фурье периодическую функцию с периодом Решение. Будем считать функцию периодической с периодом Т =2. Построим график.
Проверив выполнение условий Дирихле для функции Интеграл, стоящий в правой части последнего равенства, определяется по частям:
Если Это равенство имеет место лишь в точках непрерывности функции
Задача 6. Разложить в ряд Фурье по косинусам функцию f(x), графически заданную на промежутке [0; 2] (получить первые 4 гармоники разложения).
Решение. По условию функция – четная, задана на отрезке [0; 2] = [0; l ], следовательно, ее график на промежутке [–2; 0] симметричен заданному графику относительно оси ординат и период функции T = 2 l =4 (длина промежутка [–2; 2]). Ряд Фурье для четной периодической функции
где Поскольку вид функции
где Возьмем m = 10,
Вычислим коэффициенты ряда a 0, a 1, a 2, a 4.
Подставляем найденные коэффициенты в формулу (1) и получаем аппроксимацию функции частичной суммой ряда s 3(x):
Для сравнения с функцией f (x) построим на промежутке [0; 2] график заданной функции f (x) и график полученной аппроксимации
Если в аппроксимацию s n(x) включить сумму большего числа гармоник, например, 5, то графики s 5(x) и функции f (x) практически совпадают:
Ответ:
Варианты контрольной работы по теме «Ряды Фурье» Задача 1. Построить эскиз графика, разложить в ряд Фурье следующие функции, периодические с периодом
Задача 2. Разложить в ряд Фурье функцию
Задача3. Разложить в ряд Фурье периодическую функцию
Задача4 Разложить в ряд Фурье функцию
Задача 5. Разложить в комплексный ряд Фурье периодическую функцию с периодом
Задача 6. Разложить в ряд Фурье функцию f(x), графически заданную на промежутке [0; l ] (получить первые гармоники разложения).
Разложить в ряд Фурье по синусам функцию f(x), графически заданную на промежутке [0; π] (получить первые 4 гармоники разложения).
1. Разложить в ряд Фурье по косинусам функцию f(x), графически заданную на промежутке [0; 1] (получить первые 4 гармоники разложения).
2. Разложить в ряд Фурье по синусам функцию f(x), графически заданную на промежутке [0; 2] (получить первые 4 гармоники разложения).
3. Разложить в ряд Фурье по косинусам функцию f(x), графически заданную на промежутке [0; 2,5] (получить первые 4 гармоники разложения).
4. Разложить в ряд Фурье по синусам функцию f(x), графически заданную на промежутке [0; 3] (получить первые 4 гармоники разложения).
5. Разложить в ряд Фурье по косинусам функцию f(x), графически заданную на промежутке [0; π] (получить первые 4 гармоники разложения).
6. Разложить в ряд Фурье по синусам функцию f(x), графически заданную на промежутке [0; 4] (получить первые 4 гармоники разложения).
7. Разложить в ряд Фурье по косинусам функцию f(x), графически заданную на промежутке [0; 5] (получить первые 4 гармоники разложения).
8. Разложить в ряд Фурье по синусам функцию f(x), графически заданную на промежутке [0; π] (получить первые 4 гармоники разложения).
9. Разложить в ряд Фурье по синусам функцию f(x), графически заданную на промежутке [0; 1] (получить первые 4 гармоники разложения).
Рекомендуемая литература
1. Письменный, Д.Т. Конспект лекций по высшей математике. В 2 ч. Ч. 1 / Д.Т. Письменный. –М.: Айрис-пресс, 2003. – 288 с. 2. Щипачев, В.С. Высшая математика: учебник для вузов / В.С. Щипачев.– М.: Высш. шк., 1998.– 479 с. 3.Берман Г.Н. Сборник задач по курсу математического анализа: Уч. пособие.- 22-изд., перераб.- СПб., Изд-во «Профессия», 2005.-432с. 4. Щипачев, В.С. Задачник по высшей математике / В.С. Щипачев.– М.: Высш. шк., 2001.– 304 с.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 2110; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.102 (0.01 с.) |


 , отвечающих равноотстоящим значениям аргумента x. По этим ординатам коэффициенты можно приближенно вычислить, пользуясь методами изложенными выше. Но вычисления здесь оказываются довольно громоздкими, и для того чтобы упростить и, так сказать, автоматизировать их, придумано много различных приемов, один из которых мы и предлагается.
, отвечающих равноотстоящим значениям аргумента x. По этим ординатам коэффициенты можно приближенно вычислить, пользуясь методами изложенными выше. Но вычисления здесь оказываются довольно громоздкими, и для того чтобы упростить и, так сказать, автоматизировать их, придумано много различных приемов, один из которых мы и предлагается. , имеющую период
, имеющую период  .
.
 , отрезок
, отрезок  этого ряда.
этого ряда. .
. по формуле (3)
по формуле (3)
 найдем аналогичным образом
найдем аналогичным образом
 .
. или
или  .
. =
=  , а на концах отрезка в точках
, а на концах отрезка в точках  и
и 
 =
= 

 , заданную на отрезке
, заданную на отрезке  сначала по синусам, затем по косинусам.
сначала по синусам, затем по косинусам.
 нечетным образом, получим функцию, ряд Фурье для которой составлен в §2, пример 2.
нечетным образом, получим функцию, ряд Фурье для которой составлен в §2, пример 2.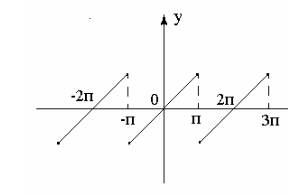
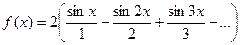

 четным образом. Построим график
четным образом. Построим график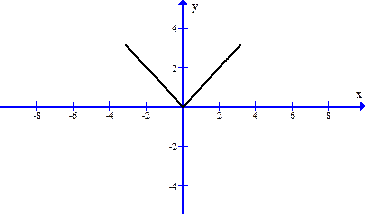
 . Найдем
. Найдем 
 =
= 

 , с периодом Т =6.
, с периодом Т =6.
 .
.
 или
или  . Это равенство имеет место во всех точках, кроме точек -3 и 3. В каждой из этих точек сумма ряда равна среднему арифметическому ее предельных значений справа и слева, то есть
. Это равенство имеет место во всех точках, кроме точек -3 и 3. В каждой из этих точек сумма ряда равна среднему арифметическому ее предельных значений справа и слева, то есть  .
.

 . Построить график S5(x).
. Построить график S5(x). , T =2, l =1. Построим эскиз графика этой функции
, T =2, l =1. Построим эскиз графика этой функции
 .
. .
.


 Подставляя коэффициенты в формулу ряда, получаем
Подставляя коэффициенты в формулу ряда, получаем  или
или  Это равенство имеет место во всех точках, кроме точек 1 и 3. В каждой из этих точек сумма ряда равна среднему арифметическому ее предельных значений справа и слева, то есть
Это равенство имеет место во всех точках, кроме точек 1 и 3. В каждой из этих точек сумма ряда равна среднему арифметическому ее предельных значений справа и слева, то есть 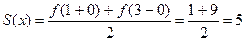 .
.
 , определенную следующим образом:
, определенную следующим образом:  . Построить амплитудно-частотный спектр.
. Построить амплитудно-частотный спектр.
 , переходим к вычислению коэффициентов Фурье по формуле
, переходим к вычислению коэффициентов Фурье по формуле  .
.
 ;
; 
 , то полученные формулы не дают результата. Поэтому коэффициент
, то полученные формулы не дают результата. Поэтому коэффициент  надо вычислить иначе׃
надо вычислить иначе׃  , так как интеграл от нечетной функции по симметричному промежутку равен нулю. Окончательно получим
, так как интеграл от нечетной функции по симметричному промежутку равен нулю. Окончательно получим 
 , где k - любое нечетное число, сумма ряда равна нулю. Построим амплитудно-частотный спектр
, где k - любое нечетное число, сумма ряда равна нулю. Построим амплитудно-частотный спектр

 , (1)
, (1) ,
,  . (2)
. (2) ,
, – середина k -го отрезка разбиения промежутка интегрирования [ a; b ], k = 1, 2, …, m, h – длина шага разбиения промежутка интегрирования:
– середина k -го отрезка разбиения промежутка интегрирования [ a; b ], k = 1, 2, …, m, h – длина шага разбиения промежутка интегрирования:  .
. , т.е. разобъем отрезок [0; 2] на 10 равных частей точками
, т.е. разобъем отрезок [0; 2] на 10 равных частей точками  и считаем с графика значения функции в серединах полученных отрезков. Чтобы вычислить коэффициенты a 0, a 1, a 2, a 4 для первых 4 гармоник разложения функции в ряд Фурье по формулам (2), построим таблицу значений функции f (x) и
и считаем с графика значения функции в серединах полученных отрезков. Чтобы вычислить коэффициенты a 0, a 1, a 2, a 4 для первых 4 гармоник разложения функции в ряд Фурье по формулам (2), построим таблицу значений функции f (x) и  в полученных точках:
в полученных точках:



 ;
;



 :
:

 ,
,  .
.









 , заданную формулой на отрезке
, заданную формулой на отрезке  , с периодом Т =2 l. Построить график частичной суммы при n=5.
, с периодом Т =2 l. Построить график частичной суммы при n=5. . Построить график частичной суммы S4(x).
. Построить график частичной суммы S4(x).









 ,
,  . Построить амплитудно-частотный спектр.
. Построить амплитудно-частотный спектр.






















