
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Равномерная сходимость функциональных рядовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Сходящийся в некотором промежутке X функциональный ряд Теорема 1 (признак Вейерштрасса). Дан ряд (1.1). Если существует такой знакоположительный сходящийся числовой ряд
что Ряд (2.1) в этом случае называется мажорирующим рядом или мажорантой, а ряд (1.1) – мажорируемым сходящимся рядом (2.1). Пример. Установить равномерную сходимость ряда Ñ Рассмотрим ряд
Пример. Показать, что ряд Ñ Для значений Задачи для самостоятельного решения Пользуясь признаком Вейерштрасса, доказать равномерную сходимость следующих функциональных рядов в указанных промежутках. 20. 23.
СВОЙСТВА РАВНОМЕРНО СХОДЯЩИХСЯ ФУНКЦИОНАЛЬНЫХ РЯДОВ Теорема 2. Если члены ряда (1.1) – функции непрерывные в некотором промежутке X и ряд сходится в этом промежутке равномерно, то сумма его Теорема 3. Если члены ряда (1.1) –функции непрерывные в X и ряд сходится равномерно в X, то ряд можно почленно интегрировать на любом отрезке Теорема 4. Если 1) ряд (1.1) сходится в некотором промежутке X к S (x); 2) Т.е. Пример. Исходя из соотношения Ñ Т.к. члены ряда
12.4. СТЕПЕННЫЕ РЯДЫ. СВОЙСТВА СТЕПЕННЫХ РЯДОВ Степенным рядом называется ряд вида
т.е. ряд, членами которого являются степенные функции. Всякий степенной ряд (4.1) сходится в интервале Если R = 0, то ряд (4.1) сходится только в точке x = 0. Если
Более общий вид степенного ряда:
Интервал сходимости этого ряда симметричен относительно точки Теорема 5. На всяком отрезке Теорема 6. Степенной ряд (4.1) можно почленно интегрировать на любом отрезке Т.о., если Теорема 7. Ряд (4.1) можно почленно дифференцировать в каждой точке x его интервала сходимости сколько угодно раз, при этом радиус сходимости ряда не меняется.
Пример. Найти сумму ряда Ñ Обозначим сумму этого ряда через Интервал сходимости этого ряда (-1, 1). На основании теоремы 7 его можно почленно дифференцировать в каждой точке интервала (-1, 1):
Справа в этом равенстве – сумма геометрической прогрессии. Если Пример. Найти сумму ряда Ñ Обозначим сумму ряда через
Этот ряд сходится в интервале (-1, 1). На основании теоремы 6 его можно почленно интегрировать на любом отрезке
Итак, Задачи для самостоятельного решения Найти сумму ряда в № 25-31. 25. 27. 30. РЯДЫ ТЕЙЛОРА И МАКЛОРЕНА. РАЗЛОЖЕНИЕ ФУНКЦИЙ В РЯД ТЕЙЛОРА И МАКЛОРЕНА Пусть функция
называется рядом Тейлора для функции f (x). Если же для всех значений x из некоторой окрестности т.
то f (x) называется разложимой в ряд Тейлора в окрестности т.
и называется рядом Маклорена. Теорема 8. Для того, чтобы функция
Теорема 9. Если
То же самое в символической записи:
При разложении 1) Непосредственное разложение 2) Использование готовых разложений:
Пример. Разложить Ñ Решим эту задачу двумя способами. I способ. Используем непосредственное разложение функции в ряд Тейлора:1)
……………………………………………………
…………………………………………………… Вычислим найденные производные в т. x = 2:
Составим формально ряд Тейлора:
б) Найдем область сходимости ряда (5.2), используя признак Даламбера:
Этот результат будет справедлив при любых x, следовательно, ряд (5.2) сходится на всей числовой оси: в) Докажем, что при всех x ряд (5.2) сходится к
II способ. Разложим
В ряд Маклорена для cos x
справа и слева вместо x подставим
(т.к. в (5/3) При разложении функции в ряд часто используют почленное дифференцирование и интегрирование рядов. Пример. Разложить в ряд Маклорена Ñ Предварительно разложим в ряд Маклорена функцию
Поэтому
Задачи для самостоятельного решения Следующие функции разложить в ряд Маклорена 33. 39. 44. Следующие функции разложить в ряд Тейлора в окрестности т. Указать область сходимости найденного ряда к своей сумме. 48. 52. 55. ПРИЛОЖЕНИЯ СТЕПЕННЫХ РЯДОВ Если некоторое число S разложено в ряд
и то поправка на отбрасывание всех остальных членов выразится остатком
Как произвести оценку погрешности? 1)Если ряд (6.1) – знакочередующийся, то остаток D имеет знак своего первого члена 2) Если ряд (6.1) – знакоположительный, то остаток D оценивают либо с помощью остаточного члена формулы Тейлора, либо пытаются найти легко суммируемый тоже знакоположительный ряд, члены которого были бы больше членов интересующего нас остатка и оценивают остаток ряда (6.1) суммой найденного ряда. Обычно ищут десятичное приближение числа S, в то время как члены ряда могут и не быть десятичными дробями. При обращении их в десятичную дробь возникает новая погрешность, которую тоже нужно учесть. Пример. Какова величина допущенной ошибки, если приближенно положить Ñ Ошибка будет суммой знакоположительного ряда
а) Оценим эту ошибку, заменив члены ряда (6.2) членами геометрической прогрессии, которые будут больше членов ряда (6.2)
б) оценим эту же ошибку с помощью остаточного члена формулы Маклорена
Пример. Вычислить Ñ Проинтегрируем полученное разложение на [0, 2]:
Получили знакочередующийся ряд. Если для вычисления интеграла Пример. Найти общее решение дифференциального уравнения Ñ Т.к. x = 0 не является особой точкой для данного дифференциального уравнения, то решение его можно искать в виде ряда
Продифференцируем ряд (6.4) дважды:
Подставим в уравнение вместо
Приравнивая коэффициенты при всех степенях x к нулю, получим:
Пример. Применяя метод последовательных дифференцирований, найти 5 членов разложения в ряд решения дифференциального уравнения
Ñ Точка x = 0 не является особой точкой данного дифференциального уравнения, поэтому решение можно искать в виде:
(разложение в окрестности x = 0!). Здесь Из уравнения Из уравнения
Подставим в (6.6) Задачи для самостоятельного решения 57. Вычислить приближенное значение 58. Вычислить приближенное значение Вычислить приближенно с указанной степенью точности D. 59. 62. Следующие интегралы вычислить с точностью до 0,001. 65. 69. Вычислить приближенно 70. Найти 6 первых членов разложения в степенной ряд решения дифференциального уравнения
71. Записать в виде степенного ряда частное решение дифференциального уравнения Записать в виде степенного ряда общее решение дифференциального уравнения. 72. 73. 75. Найти 3 члена разложения в ряд частного решения уравнения
Ответы к задачам главы 12 1. [-1; 1] 2. (-1; 1) 3. 7. 13.[-6;-4] 14. 17. 25. 28. 31. a) 34. 37. 39. 40. 42. 44. 46. 47. 49. 50. 52. 54. 56. 67. 0,481 68. 2,835 69. 0,3230, D=0,0001 70. 71. 72. 73. 74.
75.
Г Л А В А 13 РЯДЫ ФУРЬЕ. ИНТЕРАЛ ФУРЬЕ
|
||||||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 2036; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.162.107 (0.013 с.) |

 называется равномерно сходящимся в этом промежутке к
называется равномерно сходящимся в этом промежутке к  , если
, если 
 .
.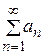 (2.1)
(2.1) , то ряд (1.1) сходится равномерно в промежутке X.
, то ряд (1.1) сходится равномерно в промежутке X. на любом отрезке.
на любом отрезке. . Он является знакоположительным, сходящимся (обобщенный гармонический,
. Он является знакоположительным, сходящимся (обобщенный гармонический, 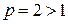 ). Для
). Для  справедливо неравенство
справедливо неравенство . Это значит, что ряд
. Это значит, что ряд  , а значит сходится равномерно на любом отрезке.#
, а значит сходится равномерно на любом отрезке.# сходится равномерно на [-1,1].
сходится равномерно на [-1,1]. очевидно
очевидно  . Ряд
. Ряд  - знакоположительный, сходящийся и, следовательно, по признаку Вейерштрасса ряд
- знакоположительный, сходящийся и, следовательно, по признаку Вейерштрасса ряд 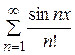 ,
,  , [-3, 3]. 22.
, [-3, 3]. 22.  .
. ,
, 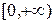 . 24.
. 24. 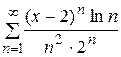 , [0, 4].
, [0, 4]. . Иначе говоря:
. Иначе говоря:  .
. - функции непрерывные в X. 3) Ряд
- функции непрерывные в X. 3) Ряд 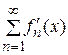 сходится равномерно в X, то ряд (1.1) можно почленно дифференцировать в каждой точке промежутка X.
сходится равномерно в X, то ряд (1.1) можно почленно дифференцировать в каждой точке промежутка X. .
. ,найти сумму ряда
,найти сумму ряда  .
. непрерывны в
непрерывны в  и ряд сходится равномерно в этом промежутке по признаку Вейерштрасса (теорема1):
и ряд сходится равномерно в этом промежутке по признаку Вейерштрасса (теорема1):  , т.е. ряд
, т.е. ряд  мажорируем сходящимся рядом
мажорируем сходящимся рядом  , то ряд
, то ряд  и
и 

 .#
.# (4.1)
(4.1) . R называется радиусом сходимости ряда (4.1).
. R называется радиусом сходимости ряда (4.1).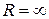 , то ряд (4.1) сходится на всей числовой оси. Если
, то ряд (4.1) сходится на всей числовой оси. Если  , то интервалом сходимости является конечный интервал с центром в точке x = 0.
, то интервалом сходимости является конечный интервал с центром в точке x = 0. . (4.2)
. (4.2) :
:  .
. ряд (4.1) сходится равномерно.
ряд (4.1) сходится равномерно. .
.

 .
. .
.


 , то
, то  , откуда
, откуда 
 . Зная, что
. Зная, что 
 .#
.#


 .
.


 . Сумма последнего ряда – сумма геометрической прогрессии, для которой
. Сумма последнего ряда – сумма геометрической прогрессии, для которой  . Таким образом,
. Таким образом,  . Продифференцируем обе части этого равенства:
. Продифференцируем обе части этого равенства:  (производная интеграла с переменным верхним пределом интегрирования по этому пределу).
(производная интеграла с переменным верхним пределом интегрирования по этому пределу).  .
. . #
. # 26.
26. 
 28.
28.  29.
29. 
 31. Исходя из соотношения
31. Исходя из соотношения  , найти сумму ряда: а)
, найти сумму ряда: а)  ; б)
; б)  . 32. Доказать, что ряд
. 32. Доказать, что ряд  сходится равномерно на
сходится равномерно на  имеет в т.
имеет в т.  и некоторой ее окрестности производные любого порядка. Ряд
и некоторой ее окрестности производные любого порядка. Ряд
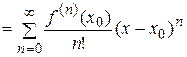 (5.1)
(5.1)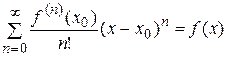 ,
, ). Если x = 0, то ряд Тейлора имеет вид
). Если x = 0, то ряд Тейлора имеет вид
 .
. - остаточный член формулы Тейлора. Записанный в форме Лагранжа, он имеет вид:
- остаточный член формулы Тейлора. Записанный в форме Лагранжа, он имеет вид:  ,
, 

 имеет в некотором промежутке, содержащем т.
имеет в некотором промежутке, содержащем т.  , то
, то 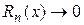 при
при  и значит
и значит 
 .
. для любых n, вычисляют
для любых n, вычисляют  и подставляют найденные значения в (5.1); b) находят область сходимости ряда (5.1); c) выясняют, для каких значений x из области сходимости ряда
и подставляют найденные значения в (5.1); b) находят область сходимости ряда (5.1); c) выясняют, для каких значений x из области сходимости ряда  .
.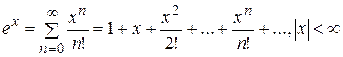


 .
.
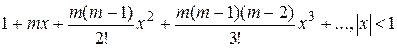
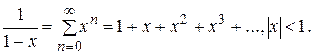
 в ряд Тейлора в окрестности т. x = 2.
в ряд Тейлора в окрестности т. x = 2.
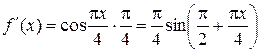 ;
;

 …,
…, ,…
,…
 (5.2)
(5.2)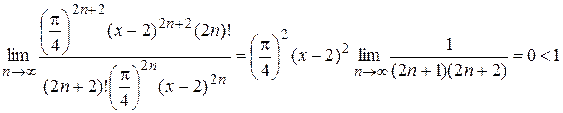
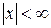 .
.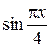 , для чего достаточно показать, что
, для чего достаточно показать, что 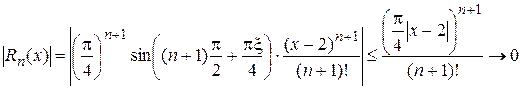 при
при  . Как результат решения задачи можем записать:
. Как результат решения задачи можем записать: ,
,  .
.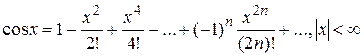 (5.3)
(5.3) , получим:
, получим:
 ; (5.4)
; (5.4) #
# .
. , для чего в разложении
, для чего в разложении  заменим x на
заменим x на  .
.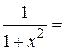

 .
.



 (получившийся ряд сходится и в граничных точках). #
(получившийся ряд сходится и в граничных точках). # ; 34.
; 34.  35.
35.  ; 36.
; 36.  ; 37.
; 37.  ; 38.
; 38.  ;
; ; 40.
; 40. 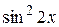 . 41.
. 41. 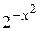 ; 42.
; 42.  ; 43.
; 43.  .
.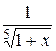 ; 45.
; 45. 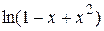 ; 46.
; 46.  ; 47.
; 47. 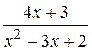 .
. . 49.
. 49.  . 50.
. 50.  . 51.
. 51.  .
.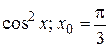 . 53.
. 53.  . 54.
. 54.  .
. . 56.
. 56.  .
.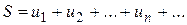 (6.1)
(6.1) ,
, .
. и
и  .
. ?
? . (6.2)
. (6.2)
 .
.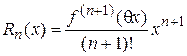 . В нашем случае
. В нашем случае 
 . #
. # с точностью до 0,001 (предполагаем, что
с точностью до 0,001 (предполагаем, что  ).
). .
.
 (6.3)
(6.3) , которая получается за счет отбрасывания членов ряда, начиная с пятого, не будет превосходить первого из отброшенных членов, т.е.
, которая получается за счет отбрасывания членов ряда, начиная с пятого, не будет превосходить первого из отброшенных членов, т.е.  . Вычисления нужно вести с 4 знаками после запятой, тогда ошибка
. Вычисления нужно вести с 4 знаками после запятой, тогда ошибка  , которая получается при обращении II, III, и IV членов ряда (6.3) в десятичные дроби будет меньше
, которая получается при обращении II, III, и IV членов ряда (6.3) в десятичные дроби будет меньше 
 . Общая ошибка
. Общая ошибка  .
.  . Результат округлен до III знака после запятой. #
. Результат округлен до III знака после запятой. # в виде степенного ряда.
в виде степенного ряда. (6.4)
(6.4)

 . (6.5)
. (6.5) и
и  соответственно ряды (6.4) и (6.5):
соответственно ряды (6.4) и (6.5):


 или
или
 .
. .
. ,
,  и т.д.
и т.д.
 #
# при начальных условиях
при начальных условиях  .
. (6.6)
(6.6) .
.
 ,
, ,
, .
.
 :
:  или
или  #
# , взяв 3 члена разложения в ряд Маклорена функции
, взяв 3 члена разложения в ряд Маклорена функции  , оценить погрешность.
, оценить погрешность. , взяв 3 члена разложения в ряд Маклорена функции
, взяв 3 члена разложения в ряд Маклорена функции  , оценить погрешность.
, оценить погрешность. 60.
60.  61.
61. 
 63.
63.  . 64.
. 64. 
 66.
66.  . 67.
. 67.  68.
68.  .
. , взяв 3 первых члена разложения подынтегральной функции в ряд. Оценить погрешность.
, взяв 3 первых члена разложения подынтегральной функции в ряд. Оценить погрешность. , удовлетворяющего начальным условиям:
, удовлетворяющего начальным условиям: .
. .
.
 (шесть первых членов)
(шесть первых членов) . 74.
. 74.  .
.
 6.
6. 
 8. {0} 9.
8. {0} 9.  10.
10.  11.
11.  12.
12.  15.
15.  16.
16.  18.
18.  19.
19. 
 26.
26.  27.
27. 
 . 29.
. 29.  30.
30. 
 б)
б)  33.
33. 
 35.
35.  36.
36. 
 38.
38. 

 41.
41. 
 43.
43. 
 45.
45. 

 48.
48. 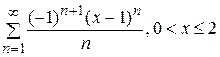

 51.
51. 
 ,
, 
 55.
55. 
 57. 1,39, D=0,01 58. 0,3090, D=0,0001 59. 0,3679 60. 0,9848 61. 4,309 62. 3,079 63. 1,609 64. 3,14159 65. 0,245 66. 0,508
57. 1,39, D=0,01 58. 0,3090, D=0,0001 59. 0,3679 60. 0,9848 61. 4,309 62. 3,079 63. 1,609 64. 3,14159 65. 0,245 66. 0,508









