
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Признаки сходимости знакопеременных рядовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Определение. Знакочередующимся рядом называется ряд вида
где Для знакочередующихся рядов имеет место следующий достаточный признак сходимости: Теорема Лейбница. Если члены знакочередующегося ряда (4.1) убывают по абсолютной величине и предел его общего члена при Т.е. для того, чтобы исследовать знакочередующийся ряд на сходимость, достаточно проверить выполнение двух условий: 1) 2) Замечание. Неравенства (3.2) могут выполняться, начиная с некоторого Примеры Исследовать на сходимость следующие ряды: 1) Решение. Т.к. члены данного ряда по абсолютной величине монотонно убывают: 2) Решение. Проверим условие (3.2): Проверим условие (3.3). Для этого необходимо вычислить Т.о., оба условия теоремы Лейбница выполняются, и, следовательно, данный ряд сходится. Определение. Ряд называется знакопеременным, если среди его членов имеются как положительные, так и отрицательные. Очевидно, знакочередующиеся ряды являются частным случаем знакопеременных. Предполагаем теперь, что в записи
имеются как положительные, так и отрицательные Теорема. (Модульный признак сходимости знакопеременных рядов). Если ряд, составленный из абсолютных величин членов данного знакопеременного ряда (3.4):
сходится, то сходится и данный ряд. Отметим, что если ряд (3.5) расходится, то отсюда не следует, что ряд (3.4) будет также расходящимся. Например, ряд В связи с этим можно ввести понятие абсолютной и условной сходимости: Определение. Знакопеременный ряд Определение. Знакопеременный ряд Например, ряд Грубо говоря, различие между абсолютно и условно сходящимися рядами заключается в следующем: абсолютно сходящиеся ряды сходятся в основном в силу того, что их члены быстро убывают, а условно сходящиеся – в результате того, что положительные и отрицательные слагаемые частично уничтожают друг друга. Свойства абсолютно и условно сходящихся рядов существенно различаются: абсолютно сходящиеся ряды по своим свойствам напоминают конечные суммы: их можно складывать, перемножать, переставлять местами члены ряда. Условно сходящиеся ряды такими свойствами не обладают. Возьмем, например, условно сходящийся ряд
Перепишем ряд в виде (произведя первое действие в каждой скобке):
Видим, что от перестановки членов ряда сумма его уменьшилась в 2 раза. Можно показать (теорема Римана), что от перестановки членов условно сходящегося ряда можно получить ряд, имеющий любую наперед заданную сумму, и даже расходящийся ряд. Примеры Исследовать ряды на абсолютную и условную сходимость. 1) Решение. Ряд, составленный из абсолютных величин членов данного ряда: 2) Решение. Составим ряд из абсолютных величин членов данного ряда: Исследуем данный знакочередующийся ряд с помощью признака Лейбница. Очевидно, что: 1) Оба пункта признака Лейбница выполнены, следовательно, данный ряд условно сходится. Задачи Исследовать ряды на абсолютную и условную сходимость: 45. 48. 51. 54. 57. Степенные ряды До сих пор мы рассматривали ряды, членами которых были числа, т.е. числовые ряды. Перейдем к рассмотрению рядов, членами которых являются функции, в частности, степенные функции с целыми неотрицательными показателями степени:
Определение. Ряд вида (4.1) называется степенным, а числа Рассматривают и степенные ряды более общего вида:
(по степеням Определение. Множество значений Структура области сходимости степенного ряда устанавливается с помощью следующей теоремы: Теорема Абеля 1) Если степенной ряд вида (4.1), т.е. по степеням 2) Если степенной ряд вида (4.1) расходится при значении Из теоремы Абеля вытекает следующая теорема. Теорема. Областью сходимости степенного ряда вида (4.2), т.е. ряда по степеням Число У некоторых рядов интервал сходимости вырождается в точку Для начала укажем способ определения интервала сходимости степенного ряда на примере ряда (4.1). Рассмотрим ряд, составленный из абсолютных величин членов этого ряда:
Т.к. при каждом конкретном Допустим, что существует
Тогда, по признаку Даламбера ряд сходится, если Следовательно, ряд (4.1) сходится абсолютно при При Замечание. Интервал сходимости можно найти, используя радикальный признак Коши (также применяя его к ряду (4.3)):
Примеры Найти области сходимости степенных рядов: 1) Решение. Рассмотрим ряд, составленный из абсолютных величин членов данного ряда
Применим к нему признак Даламбера.
Отсюда получаем интервал сходимости: Исследуем сходимость на концах интервала: При Следовательно, интервал сходимости ряда имеет вид: 2) Решение. Ряд, составленный из модулей, имеет вид:
3) Решение. Ряд, составленный из абсолютных величин членов данного ряда Следовательно, область сходимости ряда состоит из одной точки 4) Решение
Отсюда получаем интервал сходимости: При Свойства степенных рядов 1. Сумма степенного ряда 2. Степенной ряд можно почленно интегрировать по любому отрезку
3. Степенной ряд внутри интервала сходимости можно почленно дифференцировать сколь угодно раз. При этом будут получаться степенные ряды с тем же радиусом сходимости:
Задачи. Найти области сходимости степенных рядов: 60 63. 66. 69. 72. 75. 78. 81. 84. Ряды Маклорена и Тейлора Предположим, что функция
Выразим коэффициенты ряда через
…………………………………………………………….
Полагая в полученных равенствах
Подставляя значения коэффициентов
называемый рядом Маклорена. Отметим, что не все функции могут быть разложены в ряд Маклорена. Может оказаться, что ряд Маклорена, составленный формально для функции Если представить ряд Маклорена в виде Теорема. Для того чтобы ряд Маклорена сходился к функции Можно доказать, что если функция Замечание. Ряд Маклорена является частным случаем ряда Тейлора:
Ряд Тейлора тесно связан с формулой Тейлора:
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1909; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.008 с.) |

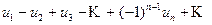 , (3.1)
, (3.1) – положительные числа.
– положительные числа. равен нулю, то ряд сходится, а его сумма не превосходит первого члена
равен нулю, то ряд сходится, а его сумма не превосходит первого члена  .
. (3.2)
(3.2)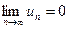 (3.3)
(3.3) .
.
 , и вообще,
, и вообще,  , а общий член ряда при
, а общий член ряда при  .
. . Доказать это неравенство достаточно сложно. Поэтому применим следующий прием: докажем, что функция
. Доказать это неравенство достаточно сложно. Поэтому применим следующий прием: докажем, что функция  монотонно убывает на некотором интервале вида
монотонно убывает на некотором интервале вида  с помощью вычисления производной и исследования функции (это уже было сделано в §2, раздел IV, пример 2). В нашем случае
с помощью вычисления производной и исследования функции (это уже было сделано в §2, раздел IV, пример 2). В нашем случае  при
при  , и функция монотонно убывает в данном промежутке. Следовательно, неравенства (3.2) выполняются для любых
, и функция монотонно убывает в данном промежутке. Следовательно, неравенства (3.2) выполняются для любых 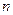 , начиная с трех.
, начиная с трех. . Используя правило Лопиталя, получим
. Используя правило Лопиталя, получим  . Следовательно, и
. Следовательно, и  .
. (3.4)
(3.4)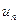 .
. (3.5)
(3.5) расходится.
расходится. является условно сходящимся (см. пример 1). А ряд
является условно сходящимся (см. пример 1). А ряд  является абсолютно сходящимся, т.к. ряд, составленный из абсолютных величин
является абсолютно сходящимся, т.к. ряд, составленный из абсолютных величин  , сходится (обобщенный гармонический при
, сходится (обобщенный гармонический при  ).
).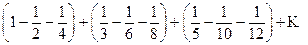


 сходится по признаку сравнения, т.к.
сходится по признаку сравнения, т.к.  , а ряд
, а ряд  – сходится (обобщенный гармонический ряд при
– сходится (обобщенный гармонический ряд при 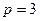 ). Следовательно, данный ряд является абсолютно сходящимся.
). Следовательно, данный ряд является абсолютно сходящимся.
 . Исследуем этот ряд на сходимость с помощью предельного признака сравнения, сравнив его с эталонным рядом
. Исследуем этот ряд на сходимость с помощью предельного признака сравнения, сравнив его с эталонным рядом  (p подберем в процессе сравнения), имеем
(p подберем в процессе сравнения), имеем  и
и 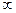 лишь при равенстве степеней числителя и знаменателя, т.е. при
лишь при равенстве степеней числителя и знаменателя, т.е. при  , следовательно, сравниваемые ряды являются расходящимися. Таким образом, ряд, составленный из модулей, расходится, и абсолютной сходимости нет.
, следовательно, сравниваемые ряды являются расходящимися. Таким образом, ряд, составленный из модулей, расходится, и абсолютной сходимости нет.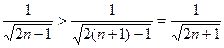 , 2)
, 2)  .
. 46.
46. 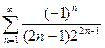 47.
47. 
 49.
49. 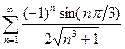 50.
50. 
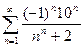 52.
52.  53.
53. 
 55.
55.  56.
56. 
 58.
58.  59.
59. 
 (4.1)
(4.1) называются коэффициентами степенного ряда.
называются коэффициентами степенного ряда. (4.2)
(4.2) ). Такой ряд не отличается существенно от ряда вида (4.1), ибо приводится к нему простой заменой переменной:
). Такой ряд не отличается существенно от ряда вида (4.1), ибо приводится к нему простой заменой переменной:  .
. , при которых степенной ряд (4.1) или (4.2) сходится, называется областью сходимости степенного ряда.
, при которых степенной ряд (4.1) или (4.2) сходится, называется областью сходимости степенного ряда. (отличном от нуля), то он сходится, и притом абсолютно, при всех значениях
(отличном от нуля), то он сходится, и притом абсолютно, при всех значениях  .
. , то он расходится при всех значениях
, то он расходится при всех значениях  .
. и с концами в точках
и с концами в точках  и
и  .
. получило название радиуса сходимости, а интервал
получило название радиуса сходимости, а интервал  – интервала сходимости степенного ряда. На концах интервала сходимости, т.е. при
– интервала сходимости степенного ряда. На концах интервала сходимости, т.е. при  и
и  вопрос о сходимости или расходимости данного ряда решается индивидуально для каждого конкретного ряда.
вопрос о сходимости или расходимости данного ряда решается индивидуально для каждого конкретного ряда. ), у других охватывает всю числовую ось (при
), у других охватывает всю числовую ось (при  ).
). (4.3)
(4.3)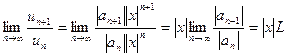 .
. (т.е. при
(т.е. при 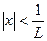 ), и расходится, если
), и расходится, если 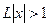 (т.е. при
(т.е. при 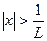 ).
). , а радиусом сходимости является число
, а радиусом сходимости является число  .
. признак Даламбера не дает ответа на вопрос о сходимости, поэтому необходимо, подставляя значения
признак Даламбера не дает ответа на вопрос о сходимости, поэтому необходимо, подставляя значения  в ряд (4.1), исследовать получающиеся числовые ряды в каждом конкретном случае.
в ряд (4.1), исследовать получающиеся числовые ряды в каждом конкретном случае.

 .
.
 .
.
 .
. исходный ряд принимает вид:
исходный ряд принимает вид: 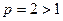 , а значит, он сходится. При
, а значит, он сходится. При  получаем абсолютно сходящийся ряд
получаем абсолютно сходящийся ряд 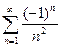 , т.к. ряд, составленный из модулей его членов, сходится.
, т.к. ряд, составленный из модулей его членов, сходится. .
. .
. .
.
 .
.
 , исследуем с помощью радикального признака Коши:
, исследуем с помощью радикального признака Коши: 
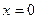 .
.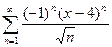
 .
. .
. исходный ряд имеет вид:
исходный ряд имеет вид: 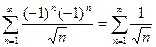 – это расходящийся ряд (обобщенный гармонический при
– это расходящийся ряд (обобщенный гармонический при  ). Подставляя
). Подставляя  . Окончательно, интервал сходимости ряда имеет вид:
. Окончательно, интервал сходимости ряда имеет вид:  .
. является непрерывной функцией во всем интервале сходимости ряда.
является непрерывной функцией во всем интервале сходимости ряда. , лежащему в интервале сходимости
, лежащему в интервале сходимости .
.
 61.
61. 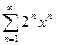 62.
62. 
 64.
64.  65.
65. 
 67.
67.  68.
68. 
 70.
70.  71.
71. 
 73.
73.  74.
74. 
 76.
76. 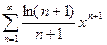 77.
77. 
 79.
79.  80.
80. 
 82.
82.  83.
83. 
 85.
85.  (Указание: при исследовании сходимости на правом конце интервала учесть, что факториалы больших чисел могут быть выражены приближенно формулой Стирлинга
(Указание: при исследовании сходимости на правом конце интервала учесть, что факториалы больших чисел могут быть выражены приближенно формулой Стирлинга  ).
). , определенная и бесконечно дифференцируемая в окрестности точки
, определенная и бесконечно дифференцируемая в окрестности точки  (5.1)
(5.1)



 ,
,  ,
,  ,
,  , …,
, …,  , откуда
, откуда ,
,  ,
,  ,
,  ,…,
,…,  ,…
,… , в (5.1), получим ряд:
, в (5.1), получим ряд: (5.2)
(5.2) , где
, где  –
–  –
–  для всех значений
для всех значений  при
при 
 , где
, где  – остаточный член формулы Тейлора, который можно записать в форме Лагранжа:
– остаточный член формулы Тейлора, который можно записать в форме Лагранжа: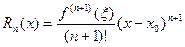 ,
,  .
.


