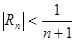Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теоремы о структуре знакопеременных рядов.Содержание книги
Поиск на нашем сайте
Обозначим
Пример A Am Po P Qo Q
Теорема Ряды P, Po, ряды Q, Qo сходятся или расходятся одновременно.
Доказательство. Так как ряд знакопеременный, то два последовательных положительных члена отделяет друг от друга конечное число отрицательных членов. То же верно и для последовательных отрицательных членов. Пусть первая серия нулей в Po:
Теорема. Если P сходится, Q – сходится, то Am сходится, т.е. ряд A сходится абсолютно. Доказательство. Так как P сходится, то Po сходится, так как Q – сходится, то Qo – сходится. Складывая сходящиеся ряды Po и (-Qo) почленно (учитывая, что
Теорема. Если P сходится и Q расходится или P расходится и Q сходится, то A расходится. Доказательство. Рассмотрим один из вариантов. Пусть P сходится и Q расходится. Тогда Po сходится. Будем доказывать от противного. Пусть A сходится, тогда, вычитая из него сходящийся ряд Po, получим сходящийся ряд Qo. Тогда по доказанной выше теореме ряд Q сходится. Противоречие. Второй вариант P расходится и Q сходится рассматривается аналогично.
Теорема. Пусть ряд A условно сходится, тогда ряды P, Q расходятся. Доказательство. Если P, Q оба сходятся, то по доказанной выше теореме Am сходится, т.е. ряд A сходится абсолютно. Противоречие. Если P сходится и Q расходится или P расходится и Q сходится, то A расходится.(по доказанной выше теореме). Противоречие. Следовательно, оба ряда P, Q расходятся. Итак, получена следующая схема.
Эта схема отражает суть теорем о структуре знакопеременных рядов.
Пример. P: Q: Пример. P: Q:
Теорема Римана. Пусть S – произвольное число (конечное или бесконечное). Тогда можно так переставить местами члены условно сходящегося знакопеременного ряда, что его сумма будет равна S.
Доказательство. Так как ряд A условно сходится, то ряды P, Q расходятся (теоремы о структуре знакопеременного ряда). Пусть для определенности S>0. Переставляем в начало ряда столько положительных членов, чтобы их сумма стала больше S, Теперь переставляем столько отрицательных членов, чтобы частичная сумма ряда стала бы меньше S. Повторяем этот процесс. Процесс осуществим для любого S, так как ряды P, Q расходятся (т.е. повторением членов можно набрать любую их сумму). С другой стороны, частичная сумма сконструированного ряда сходится именно к S. В сконструированном ряде Сам ход доказательства напоминает добавление положительных членов – гирь на одну чашку весов, пока весы не покажут вес, больший S. Последний член – гиря
Знакочередующиеся ряды.
Знакопеременный ряд называется знакочередующимся, если знаки членов ряда чередуются, т.е. ряд К знакочередующимся рядам можно применить все теоремы, доказанные выше для знакопеременных рядов. Но есть специальный, очень удобный достаточный признак сходимости знакочередующихся рядов – признак Лейбница (он не является необходимым признаком).
Признак Лейбница. Пусть 1. ряд 2. последовательность 3. Тогда 1) ряд 2) Доказательство. Рассмотрим последовательность частичных сумм с четными номерами
Т.е. последовательность
Т.е. последовательность По теореме Вейерштрасса существует Рассмотрим теперь последовательность частичных сумм с нечетными номерами
По условию По доказанному выше
Раскроем определение предела Из доказанного выше неравенства
Следствие. Доказательство. Так как остаток знакочередующегося ряда тоже знакочередующийся ряд, то его сумма по признаку Лейбница оценивается модулем его первого члена. То есть
Пример. Ряд
Функциональные ряды
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 664; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.141.47.139 (0.006 с.) |

 - положительные члены,
- положительные члены,  - отрицательные члены знакопеременного ряда. A – ряд
- отрицательные члены знакопеременного ряда. A – ряд  , Am – ряд
, Am – ряд  , P – ряд
, P – ряд  , Po – ряд A, в котором все отрицательные члены заменены нулями на тех же местах. Q – ряд
, Po – ряд A, в котором все отрицательные члены заменены нулями на тех же местах. Q – ряд  , Qo – ряд A, в котором все положительные члены заменены нулями на тех же местах.
, Qo – ряд A, в котором все положительные члены заменены нулями на тех же местах.



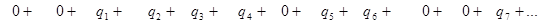

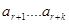 Тогда
Тогда  , т.е. k элементов в последовательности частичных сумм повторяются. Исключим их из последовательности и перенумеруем члены (это соответствует исключению серии нулей). Исключение последовательных одинаковых элементов не влияет на сходимость и предел последовательности. Далее доказательство можно провести по индукции, так как операция исключения нулей аналогична. Поэтому ряды Po и P сходятся или расходятся одновременно. Аналогичное верно и для Qo и Q.
, т.е. k элементов в последовательности частичных сумм повторяются. Исключим их из последовательности и перенумеруем члены (это соответствует исключению серии нулей). Исключение последовательных одинаковых элементов не влияет на сходимость и предел последовательности. Далее доказательство можно провести по индукции, так как операция исключения нулей аналогична. Поэтому ряды Po и P сходятся или расходятся одновременно. Аналогичное верно и для Qo и Q. ), получим сходящийся ряд. Это – ряд Am.
), получим сходящийся ряд. Это – ряд Am.
 .
.
 - сходящаяся бесконечно убывающая геометрическая прогрессия.
- сходящаяся бесконечно убывающая геометрическая прогрессия. сходящаяся бесконечно убывающая геометрическая прогрессия. Следовательно, исходный ряд A абсолютно сходится.
сходящаяся бесконечно убывающая геометрическая прогрессия. Следовательно, исходный ряд A абсолютно сходится.
 - сходящаяся бесконечно убывающая геометрическая прогрессия.
- сходящаяся бесконечно убывающая геометрическая прогрессия. расходящийся ряд (по второму признаку сравнения с гармоническим рядом). Следовательно, исходный ряд A расходится.
расходящийся ряд (по второму признаку сравнения с гармоническим рядом). Следовательно, исходный ряд A расходится. - тот член ряда, добавление которого меняет знак
- тот член ряда, добавление которого меняет знак 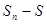 .
.  так как знакопеременный ряд условно сходится.
так как знакопеременный ряд условно сходится. . Затем добавление на другую чашку весов столько отрицательных – членов (вернее гирь, весом, равным модулям этих членов), чтобы весы показали вес, меньший S. Процесс повторяется. Вес гирь, вызывающих переход указателя весов через S, убывает до нуля, так как для условно сходящегося ряда выполняется необходимый признак сходимости. Поэтому
. Затем добавление на другую чашку весов столько отрицательных – членов (вернее гирь, весом, равным модулям этих членов), чтобы весы показали вес, меньший S. Процесс повторяется. Вес гирь, вызывающих переход указателя весов через S, убывает до нуля, так как для условно сходящегося ряда выполняется необходимый признак сходимости. Поэтому  .
. . Предполагаем, что ряд начинается с положительного члена,
. Предполагаем, что ряд начинается с положительного члена,  .
.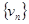 монотонно убывает
монотонно убывает

 (последовательность
(последовательность 
 ограничена сверху
ограничена сверху  .
.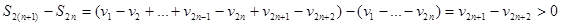
 .
. .
. .
. . Поэтому предел левой части равенства тоже существует и равен
. Поэтому предел левой части равенства тоже существует и равен .
.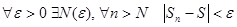 как для четных n, так и для нечетных n. Следовательно, это справедливо для любых
как для четных n, так и для нечетных n. Следовательно, это справедливо для любых  , поэтому
, поэтому  .
. . Переходя к пределу, получим
. Переходя к пределу, получим  .
. . Остаток ряда оценивается модулем первого отброшенного члена ряда.
. Остаток ряда оценивается модулем первого отброшенного члена ряда.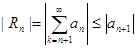 . А первый член остатка ряда и есть первый отброшенный член.
. А первый член остатка ряда и есть первый отброшенный член.
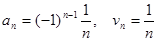 . Ряд сходится по признаку Лейбница. Ряд из модулей – расходящийся гармонический ряд. Следовательно, ряд сходится условно.
. Ряд сходится по признаку Лейбница. Ряд из модулей – расходящийся гармонический ряд. Следовательно, ряд сходится условно.