
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Краткий курс математического анализаСтр 1 из 10Следующая ⇒
Галкин С.В.
Краткий курс математического анализа В лекционном изложении для студентов МГТУ им. Н. Э. Баумана (третий семестр)
Москва 2005.
Часть1 Кратные и криволинейные интегралы, теория поля. Лекция 1. Двойной интеграл. Задача об объеме цилиндрического тела. К определенному интегралу мы пришли от задачи о площади криволинейной трапеции. К двойному интегралу мы приходим, решая задачу об объеме цилиндрического тела. - Рассмотрим, например, прямой круговой цилиндр с высотой h и радиусом основания R его объем равен - Объем цилиндра той же высоты, в основании которого лежит эллипс с полуосями - Объем цилиндра той же высоты, с площадью основания Пусть надо вычислить объем цилиндрического тела, в основании которого лежит область
Двойной интеграл [1]
Теорема существования [2]. Пусть функция
Замечание [4]. Предел этот не зависит от - способа выбора разбиения, лишь бы выполнялось условие А - выбора «отмеченных точек» на элементах разбиения, - способа измельчения разбиения, лишь бы выполнялось условие В
Свойства двойного интеграла [5].
1. Линейность б) свойство однородности Доказательство. Запишем интегральные суммы для интегралов в левых частях равенств. Они равны интегральным суммам для правых частей равенств, так как число слагаемых конечно. Затем перейдем к пределу, по теореме о предельном переходе в равенстве получим желаемый результат.
2. Аддитивность. Доказательство. Выберем разбиение области D так, чтобы ни один из элементов разбиения (первоначально и при измельчении разбиения) не содержал одновременно как элементы D1, так и элементы D2. Это можно сделать по теореме существования (замечание к теореме). Далее проводится доказательство через интегральные суммы, как в п.1.
3. 4. Если в области D выполнено неравенство Доказательство. Запишем неравенство для интегральных сумм и перейдем к пределу. Заметим, что, в частности, возможно 5. Теорема об оценке. Если существуют константы
Доказательство. Интегрируя неравенство
6. Теорема о среднем (значении интеграла). Существует точка Доказательство. Так как функция Геометрический смысл теоремы состоит в том, что существует цилиндр постоянной высоты
Лекция 3 Тройной интеграл. Лекция 4. Приложения тройного интеграла.
Задача о работе силы.
1. Организуем разбиение области- дуги AB на элементы – элементарные дуги
2. Отметим на элементах разбиения «отмеченные точки» Mi и вычислим в них значения функции 3. Построим интегральную сумму 4. Переходя к пределу при условии
Теорема существования. Пусть вектор - функция
Замечание. Предел этот не зависит от - способа выбора разбиения, лишь бы выполнялось условие А - выбора «отмеченных точек» на элементах разбиения, - способа измельчения разбиения, лишь бы выполнялось условие В
Лекция 6. Формула Грина.
Теорема (формула) Грина. Пусть G – плоская односвязная область с кусочно-гладкой границей L. Пусть функции P(x, y), Q(x, y) непрерывны и имеют непрерывные частные производные по своим переменным в области G и на L. Тогда справедлива формула Грина
Доказательство. 1) Назовем плоскую область D (в плоскости OXY) правильной, если любая прямая, параллельная координатной оси (OX или OY) пересекает область не более, чем в двух точках. Можно показать, что область G можно представить как объединение конечного числа правильных областей Тогда по свойству аддитивности двойной интеграл в правой части формулы Грина равен сумме двойных интегралов по правильным областям. Криволинейный интеграл в левой части равен сумме криволинейных интегралов по границам правильных областей, так как криволинейные интегралы по общим границам любых правильных областей различны по знаку из-за различных направлений обхода границы и взаимно уничтожаются при суммировании. Поэтому доказательство может быть проведено для правильной области G. 2) Пусть G – правильная область. Так как P, Q могут быть произвольными функциями, то формула Грина сводится двум формулам
Формула Ньютона – Лейбница. Пусть выполнены условия теоремы о полном дифференциале и пусть выражение
Тогда справедлива формула Ньютона – Лейбница
Доказательство. В теореме о полном дифференциале доказано, что потенциал можно записать в виде Лекция 8 Скалярное и векторное поля. Говорят, что в области (плоской или пространственной) задано скалярное поле j (M), если в этой области задана скалярная функция j (M).
Говорят, что в области (плоской или пространственной) задано векторное поле Например, масса или температура частиц в комнате – скалярные поля, скорость или силы взаимодействия частиц – векторные поля. В интегралах первого рода:двойных, криволинейных, поверхностных мы имели дело со скалярным полем – распределением масс точек кривой или поверхности в пространстве. В интегралах второго рода вычислялись характеристики векторных полей: работа векторного поля (силового поля) в криволинейном интеграле, поток векторного поля в поверхностном интеграле. Рассмотрим подробнее основные характеристики скалярных и векторных полей.
Скалярные поля.
Линии уровня плоского поля j (x, y) – кривые, на которых значения функции постоянны j (x, y) = С. Например, линии равной высоты, нанесенные на географической карты (h (x, y) = 0 – уровень моря, h = 7000м – немногие горные вершины, h = - 10000м – самые глубокие океанские впадины). Поверхности уровня пространственного поля j (x, y, z) – поверхности, на которых значения функции постоянны j (x, y, z) = С. Например, поверхности равной температуры или давления в атмосфере. Любая линия на поверхности уровня – это линия уровня. Пример. Задано поле Линии или поверхности различных уровней не пересекаются. Чем чаще (гуще) поверхности или линии уровня, тем интенсивнее изменение поля. Градиент поля – вектор Утверждение. Градиент скалярного поля ортогонален его поверхности уровня. Доказательство. Пусть точка (x, y, z) остается на поверхности уровня g(x, y, z) = 0 при вариациях переменных. Тогда равенство превращается в тождество, а тождество можно дифференцировать.
Вектор
Производная скалярного поля по направлению
Пример. Найти производную скалярного поля g(x, y, z) = x2 + y2 + z3 по направлению {1,3,2} в точке (1,0,4)
Векторное поле.
Векторная линия -линия, в каждой точке которой вектор поля направлен по касательной к ней. Уравнения векторной линии легко получить из условия коллинеарности векторов поля
Пример. Написать уравнения векторных линий векторного поля
Векторной трубкой называется поверхность, образованная векторными линиями.
Свойства дивергенции. 1) Линейность.
2)
3)
Лекция 9 Формула Стокса. Ротор векторного поля. Назовем ротором векторного поля
Свойства ротора. 1) Линейность
2)
3)
Теорема Стокса.
Пусть пространственно односвязная область V содержит кусочно-гладкую поверхность Пусть компоненты векторного поля Тогда справедлива формула Стокса
Замечание. Нормаль к поверхности
Доказательство теоремы Стокса.
представляет собой вектор Отсюда видно, что
(на поверхности = Используем формулу Грина для области D с ее границей
= В самом деле, на контуре Одна из частей формулы Стокса доказана.
Линейным интегралом векторного поля Линейный интеграл имеет смысл работы векторного поля при перемещении по дуге.
Циркуляцией векторного поля называется линейный интеграл по замкнутому контуру.
Вводя эти понятия, можно записать формулу Стокса в «полевой» форме
Мы определили ротор векторного поля в декартовой системе координат, однако ротор – это характеристика самого векторного поля Поэтому необходимо дать определение ротора, которое не зависит от выбора системы координат.
Инвариантное определение ротора. Рассмотрим произвольную точку M в области V. Проведем через нее поверхность
Здесь, как и ранее
Это и есть инвариантное определение ротора. Правая часть формулы – это поверхностная плотность циркуляции векторного поля (энергии в точке M вращения векторного поля или работы векторного поля при вращении вокруг некоторого направления, определяемого вектором Если направление Левая часть достигает максимума при коллинеарности направления и ротора векторного поля. Поэтому направление ротора векторного поля – это то направление, вокруг которого поверхностная плотность циркуляции векторного поля – наибольшая. Пример. Найти ротор линейной скорости вращения с постоянной угловой скоростью
Векторное поле линейной скорости
Ранее была сформулирована теорема о полном дифференциале для пространственной кривой. В ее доказательстве не хватало только одного пункта – перехода от пункта 3) к пункту 2). Все остальное доказывается аналогично случаю плоской кривой.
Оператор Гамильтона Оператор Гамильтона Применим оператор Гамильтона к скалярному полю Оператор Гамильтона представляет собой вектор-оператор. Его можно скалярно или векторно умножить на векторное поле
Это дифференциальные операции первого порядка над скалярным и векторным полями. От скалярного поля можно взять градиент, от векторного поля можно взять дивергенцию и ротор. Гармоническое поле. Скалярное поле
Векторное поле называется гармоническим, если оно потенциальное ( Теорема. Для того, чтобы векторное поле Необходимость. Если векторное поле Достаточность. Если векторное поле
Так как гармоническое поле потенциально и соленоидально, то его свойства – свойства соленоидального поля и свойства потенциального поля.
Свойства сходящихся рядов. 1. Члены сходящегося ряда можно умножить на одно и то же число k. Полученный ряд будет сходиться, а сумма его будет в k раз больше суммы исходного ряда.
Доказательство. Для второго ряда частичная сумма будет равна
2. Члены сходящегося ряда можно группировать. Полученный ряд будет сходиться, и сумма его не изменится.
Сгруппируем члены ряда, например, так
3. В сходящемся ряде можно отбросить конечное число первых членов
Запишем частичные суммы второго ряда Замечание. Ряд, полученный из исходного ряда отбрасыванием первых k членов, называется остатком ряда и обозначается
4. Для того чтобы ряд сходился необходимо и достаточно, чтобы сходился остаток ряда. (Докажите это самостоятельно, используя доказательство свойства 3). Поэтому сходимость ряда можно исследовать, «начиная с некоторого n».
5. Сходящиеся ряды можно складывать (или вычитать), получая сходящийся ряд с суммой, равной сумме (или разности) сумм исходных рядов.
Рассмотрим два сходящихся ряда
Примеры. 1. Ряд –5+7-8+100+1+0,5+0,25+0,125+… сходится. В самом деле, отбросив первых четыре члена ряда (свойства 3,4), получим сходящуюся бесконечно убывающую геометрическую прогрессию 2. Ряд 3. Ряд
Интегральный признак Коши.
Доказательство. Так как . Достаточность. Если интеграл сходится, то Необходимость. Если ряд Если ряд расходится, то и интеграл расходится и наоборот. Это легко доказывается от противного. Поэтому говорят, что несобственный интеграл и ряд сходятся или расходятся «одновременно», т.е. один из них сходится, то и другой сходится, если один расходится, то и другой расходится. Это понятие часто употребляют при сравнении рядов.
Пример. Применим интегральный признак к гармоническому ряду.
Пример. Рассмотрим «ряды Дирихле»
Интересно, что ряд Теперь становится яснее, где пролегает граница между сходящимися и расходящимися рядами. Заодно накоплена библиотека сходящихся и расходящихся рядов, которые можно использовать как эталонные при сравнении рядов. Сравнивать ряды можно с помощью признаков сравнения.
Признаки сравнения рядов. Второй признак сравнения. Пусть Доказательство. Раскроем определение предела.
Если ряд Если ряд
|
|||||||||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 393; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.131.13.37 (0.171 с.) |

 равен
равен  .
. , равен
, равен  .
. с площадью
с площадью  изменяется от точки к точке так, что конец ее описывает некоторую поверхность
изменяется от точки к точке так, что конец ее описывает некоторую поверхность 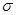 (
( ). Тогда логично разбить область
). Тогда логично разбить область  .
.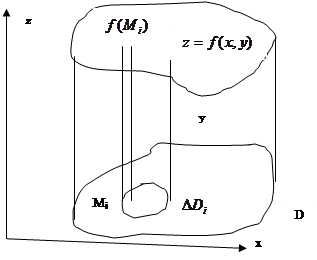


 так, чтобы эти элементы не имели общих внутренних точек и
так, чтобы эти элементы не имели общих внутренних точек и  (условие А)
2. Отметим на элементах разбиения «отмеченные точки» Mi и вычислим в них значения функции
(условие А)
2. Отметим на элементах разбиения «отмеченные точки» Mi и вычислим в них значения функции  3. Построим интегральную сумму
3. Построим интегральную сумму  , где
, где  - площадь
- площадь  (условие В), получим двойной интеграл как предел интегральных сумм:
(условие В), получим двойной интеграл как предел интегральных сумм: 
 непрерывна в замкнутой односвязной области D[3]. Тогда двойной интеграл существует как предел интегральных сумм.
непрерывна в замкнутой односвязной области D[3]. Тогда двойной интеграл существует как предел интегральных сумм.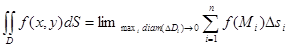 .
.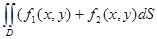 . =
. =  +
+ 
 . =
. = 
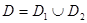 , то
, то 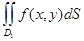 +
+ 
 -площадь области D.
-площадь области D. , то
, то 
 (неравенство можно интегрировать).
(неравенство можно интегрировать).
 , что
, что  , то
, то
 (свойство 4), получим
(свойство 4), получим  . По свойству 1 константы
. По свойству 1 константы  , что
, что  .
. непрерывна на замкнутом ограниченном множестве
непрерывна на замкнутом ограниченном множестве 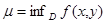 и верхняя грань
и верхняя грань  . Выполнено неравенство
. Выполнено неравенство  . Деля обе части на
. Деля обе части на  , получим
, получим  . Но число
. Но число  заключено между нижней и верхней гранью функции. Так как функция
заключено между нижней и верхней гранью функции. Так как функция  функция должна принимать это значение. Следовательно,
функция должна принимать это значение. Следовательно,  , объем которого равен объему цилиндрического тела
, объем которого равен объему цилиндрического тела 
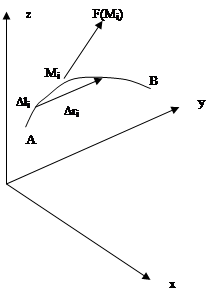
 , где
, где 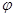 - угол между векторами. В общем случае эту формулу можно использовать для построения интегральной суммы, предполагая силу постоянной на элементе дуги
- угол между векторами. В общем случае эту формулу можно использовать для построения интегральной суммы, предполагая силу постоянной на элементе дуги  достаточно малой длины. Вместо длины малого элемента дуги можно взять длину стягивающей ее хорды
достаточно малой длины. Вместо длины малого элемента дуги можно взять длину стягивающей ее хорды  , так как эти величины – эквивалентные бесконечно малые величины при условии
, так как эти величины – эквивалентные бесконечно малые величины при условии 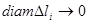 (первый семестр).
(первый семестр).
 (условие А)
(условие А)
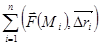 , где
, где 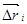 вектор, направленный по хорде, стягивающей -дугу
вектор, направленный по хорде, стягивающей -дугу  (условие В), получим криволинейный интеграл второго рода как предел интегральных сумм (и работу силы):
(условие В), получим криволинейный интеграл второго рода как предел интегральных сумм (и работу силы): . Часто обозначают
. Часто обозначают 
 непрерывна на кусочно-гладкой дуге L[12]. Тогда криволинейный интеграл второго рода существует как предел интегральных сумм.
непрерывна на кусочно-гладкой дуге L[12]. Тогда криволинейный интеграл второго рода существует как предел интегральных сумм. .
.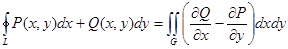 .
. .
. и
и  , каждую из которых надо доказать. Докажем первую формулу, вторая доказывается аналогично.
, каждую из которых надо доказать. Докажем первую формулу, вторая доказывается аналогично.
 =
= 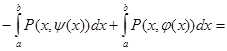 =
=  =
=
 =
= 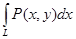
 - полный дифференциал, а функция
- полный дифференциал, а функция  - потенциал.
- потенциал. , где
, где 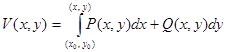 . Так как интеграл не зависит от пути интегрирования, то дугу, соединяющую точки (x1, y1), (x2, y2) можно провести через точку (x0, y0). Поэтому
. Так как интеграл не зависит от пути интегрирования, то дугу, соединяющую точки (x1, y1), (x2, y2) можно провести через точку (x0, y0). Поэтому 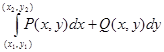 =
=  +
+  =
=  =
= 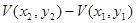 .
.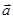 (M), если в этой области задана векторная функция
(M), если в этой области задана векторная функция  . При С > 0 поверхности уровня – однополостные гиперболоиды, при С = 0 поверхность уровня – конус, при С < 0 поверхности уровня – двуполостные гиперболоиды.
. При С > 0 поверхности уровня – однополостные гиперболоиды, при С = 0 поверхность уровня – конус, при С < 0 поверхности уровня – двуполостные гиперболоиды. .
. .
. (x, y, z) - это вектор, касательный в точке (x, y, z) к любой кривой, лежащей на поверхности уровня, проходящей через эту точку. Поэтому в точке (x, y, z) вектор градиента ортогонален всем касательным к линии уровня, проходящим через эту точку. Следовательно, он ортогонален касательной плоскости к поверхности уровня и направлен по нормали к поверхности уровня.
(x, y, z) - это вектор, касательный в точке (x, y, z) к любой кривой, лежащей на поверхности уровня, проходящей через эту точку. Поэтому в точке (x, y, z) вектор градиента ортогонален всем касательным к линии уровня, проходящим через эту точку. Следовательно, он ортогонален касательной плоскости к поверхности уровня и направлен по нормали к поверхности уровня.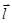 определяется как
определяется как  . Известно из теории функций многих переменных (выпуск V учебника), что производная по направлению есть проекция градиента на данное направление
. Известно из теории функций многих переменных (выпуск V учебника), что производная по направлению есть проекция градиента на данное направление .
. .
. 
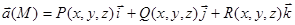 и касательной
и касательной 
 .
.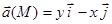
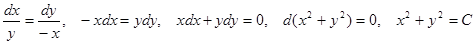 - линии уровня – окружности (С>0).
- линии уровня – окружности (С>0).

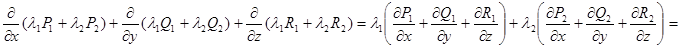
 .
. , где
, где  - постоянное векторное поле.
- постоянное векторное поле.
 , где
, где  - скалярное поле.
- скалярное поле. =
=  =
=  .
.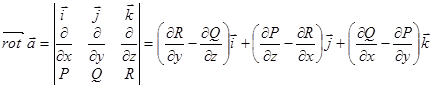
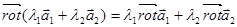
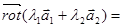
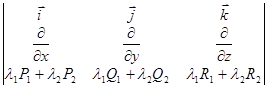 =
= 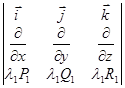 +
+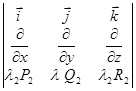 =
= 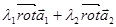 .
.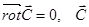 - постоянное векторное поле.
- постоянное векторное поле.
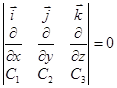
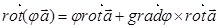
 =
=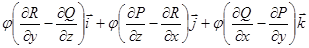 +
+ 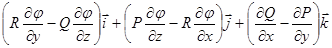 =
= 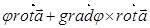 .
.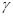 .
.
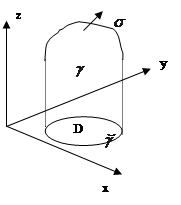

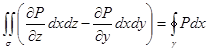 - часть формулы Стокса, в которой содержится только компонента P.
Предположим, что поверхность
- часть формулы Стокса, в которой содержится только компонента P.
Предположим, что поверхность 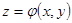 . Тогда нормаль к поверхности
. Тогда нормаль к поверхности

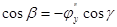 . Вспомним еще, что
. Вспомним еще, что 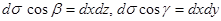 .
.
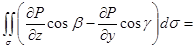
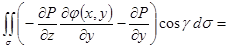
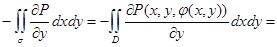
 . Ее можно записать в виде
. Ее можно записать в виде . Нам понадобится только та ее часть, которая относится к функции P
. Нам понадобится только та ее часть, которая относится к функции P 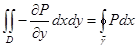 . Продолжаем равенство дальше.
. Продолжаем равенство дальше.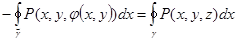 .
.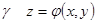 , а переменные x, y на том и другом контуре те же, так как контур
, а переменные x, y на том и другом контуре те же, так как контур 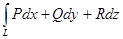 .
.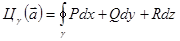 .
.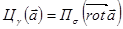 .
.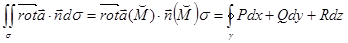 .
.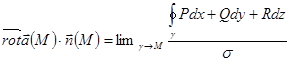
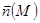 ). Левая часть – это проекция ротора на это направление.
). Левая часть – это проекция ротора на это направление.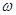
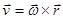 .
.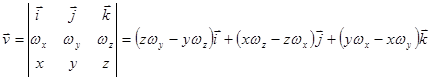 ,
,
 .
. .
.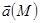 .
.
 - уравнение Лапласа.
- уравнение Лапласа. ), а потенциал
), а потенциал  .
. было гармоническим, необходимо и достаточно чтобы оно было соленоидальным и потенциальным.
было гармоническим, необходимо и достаточно чтобы оно было соленоидальным и потенциальным. .
. . Следовательно, поле потенциально и его потенциал удовлетворяет уравнению Лапласа, поэтому векторное поле – гармоническое.
. Следовательно, поле потенциально и его потенциал удовлетворяет уравнению Лапласа, поэтому векторное поле – гармоническое. . По теореме о предельном переходе в равенстве
. По теореме о предельном переходе в равенстве  .
. . Видно, что частичные суммы группированного ряда представляют собой подпоследовательность последовательности частичных сумм исходного ряда. Так как последовательность сходится, то и подпоследовательность сходится к тому же пределу.
. Видно, что частичные суммы группированного ряда представляют собой подпоследовательность последовательности частичных сумм исходного ряда. Так как последовательность сходится, то и подпоследовательность сходится к тому же пределу. . Полученный ряд будет сходиться, а его сумма будет меньше суммы исходного ряда на B.
. Полученный ряд будет сходиться, а его сумма будет меньше суммы исходного ряда на B. . По теореме о предельном переходе в равенстве
. По теореме о предельном переходе в равенстве  .
.
 и
и  . Рассмотрим ряд
. Рассмотрим ряд  , где
, где  .
.  . Переходя к пределу в равенстве, получим
. Переходя к пределу в равенстве, получим  .
. расходится. Он представляет собой сумму двух рядов: сходящейся геометрической прогрессии (нечетные члены) и гармонического ряда (четные члены). Если бы этот ряд сходился, то, вычитая из него почленно сходящийся ряд
расходится. Он представляет собой сумму двух рядов: сходящейся геометрической прогрессии (нечетные члены) и гармонического ряда (четные члены). Если бы этот ряд сходился, то, вычитая из него почленно сходящийся ряд  , мы должны были бы по свойству 5 получить сходящийся ряд. А получаем расходящийся гармонический ряд. Следовательно, исходный ряд расходится.
, мы должны были бы по свойству 5 получить сходящийся ряд. А получаем расходящийся гармонический ряд. Следовательно, исходный ряд расходится. сходится. Рассмотрим сходящийся ряд
сходится. Рассмотрим сходящийся ряд  . Группируем его члены
. Группируем его члены , получаем исходный ряд. Следовательно, он сходится (свойство 2), и его сумма равна 1.
, получаем исходный ряд. Следовательно, он сходится (свойство 2), и его сумма равна 1.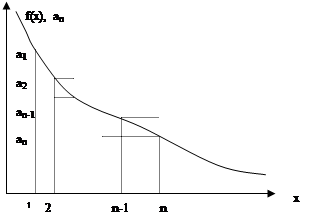






 определена непрерывная, не возрастающая функция f(x), такая, что
определена непрерывная, не возрастающая функция f(x), такая, что  .
Тогда ряд
.
Тогда ряд  .
.
 - это площадь под графиком функции
- это площадь под графиком функции  при
при 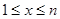 .
. (сумма площадей прямоугольников) ограничивает площадь под графиком функции снизу, а
(сумма площадей прямоугольников) ограничивает площадь под графиком функции снизу, а  ограничивает ее сверху, то
ограничивает ее сверху, то  .
. , поэтому последовательность
, поэтому последовательность  ограничена сверху. Так как эта последовательность не убывает, то по теореме Вейерштрасса
ограничена сверху. Так как эта последовательность не убывает, то по теореме Вейерштрасса  . Поэтому ряд
. Поэтому ряд  при
при  . Поэтому последовательность
. Поэтому последовательность  (неубывающая, так как
(неубывающая, так как  ) ограничена сверху. Следовательно, по теореме Вейерштрасса
) ограничена сверху. Следовательно, по теореме Вейерштрасса  , т.е. несобственный интеграл сходится.
, т.е. несобственный интеграл сходится. - интеграл расходится, поэтому и гармонический ряд расходится.
- интеграл расходится, поэтому и гармонический ряд расходится. . Название взято в кавычки, так неизвестно, рассматривал ли эти ряды Дирихле, но оно устоялось за долгие годы.
. Название взято в кавычки, так неизвестно, рассматривал ли эти ряды Дирихле, но оно устоялось за долгие годы. . Ясно, что интеграл сходится при p>1 и расходится при P<1. Случай p=1 рассмотрен выше (расходящийся гармонический ряд). Отсюда следует вывод
. Ясно, что интеграл сходится при p>1 и расходится при P<1. Случай p=1 рассмотрен выше (расходящийся гармонический ряд). Отсюда следует вывод .
. , интегралы
, интегралы  расходятся (проверьте по интегральному признаку).
расходятся (проверьте по интегральному признаку). . Тогда ряды
. Тогда ряды 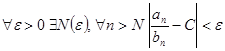 .
. .
. сходится (
сходится ( , ряд
, ряд  сходится (свойство сходящихся рядов), тогда по 1 признаку сравнения ряд
сходится (свойство сходящихся рядов), тогда по 1 признаку сравнения ряд 


