
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Соленоидальное поле и его свойства.Содержание книги
Поиск на нашем сайте
Векторное поле Свойства соленоидального поля. 1) Для того чтобы поле было соленоидальным, необходимо и достаточно, чтобы поток через любую замкнутую поверхность равнялся нулю.
Необходимость следует из формулы Остроградского – Гаусса, достаточность – из инвариантного определения дивергенции.
2) Поток соленоидального поля через любую поверхность, окружающую изолированный источник или сток, один и тот же.
поток векторного поля через границы этих областей равен нулю.
Складывая эти выражения, получим
3) Поток соленоидального поля через произвольное сечение векторной трубки один и тот же.
Следствие. Векторные линии соленоидального поля не могут начинаться и заканчиваться внутри поля. В самом деле, иначе конечный поток приходился бы на нулевую площадь источника или стока, что требовало бы бесконечной мощности источника или стока.
Лекция 9 Формула Стокса. Ротор векторного поля. Назовем ротором векторного поля
Свойства ротора. 1) Линейность
2)
3)
Теорема Стокса.
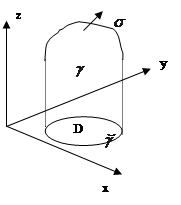
Пусть пространственно односвязная область V содержит кусочно-гладкую поверхность Пусть компоненты векторного поля Тогда справедлива формула Стокса
Замечание. Нормаль к поверхности
Доказательство теоремы Стокса.
представляет собой вектор Отсюда видно, что
(на поверхности = Используем формулу Грина для области D с ее границей
= В самом деле, на контуре Одна из частей формулы Стокса доказана.
Линейным интегралом векторного поля Линейный интеграл имеет смысл работы векторного поля при перемещении по дуге.
Циркуляцией векторного поля называется линейный интеграл по замкнутому контуру.
Вводя эти понятия, можно записать формулу Стокса в «полевой» форме
Мы определили ротор векторного поля в декартовой системе координат, однако ротор – это характеристика самого векторного поля Поэтому необходимо дать определение ротора, которое не зависит от выбора системы координат.
Инвариантное определение ротора. Рассмотрим произвольную точку M в области V. Проведем через нее поверхность
Здесь, как и ранее
Это и есть инвариантное определение ротора. Правая часть формулы – это поверхностная плотность циркуляции векторного поля (энергии в точке M вращения векторного поля или работы векторного поля при вращении вокруг некоторого направления, определяемого вектором Если направление Левая часть достигает максимума при коллинеарности направления и ротора векторного поля. Поэтому направление ротора векторного поля – это то направление, вокруг которого поверхностная плотность циркуляции векторного поля – наибольшая. Пример. Найти ротор линейной скорости вращения с постоянной угловой скоростью
Векторное поле линейной скорости
Ранее была сформулирована теорема о полном дифференциале для пространственной кривой. В ее доказательстве не хватало только одного пункта – перехода от пункта 3) к пункту 2). Все остальное доказывается аналогично случаю плоской кривой.
|
||||||||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 2135; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |

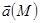 называется соленоидальным в области V, если в любой точке M этой области
называется соленоидальным в области V, если в любой точке M этой области 
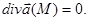




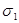 и
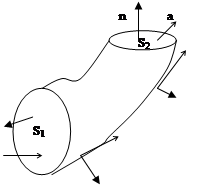
и 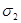 , окружающие изолированный источник (сток). Будем считать векторное поле соленоидальным в пространственной области между поверхностями. Рассечем поверхности плоскостью P и выберем на ней «верхнюю» сторону плоскости и «нижнюю» сторону, введем на плоскости вектор нормали от «нижней» стороны к «верхней». Плоскость разделяет поверхности на «верхние» и «нижние» части. Обозначим на них направления внешних нормалей к поверхностям.
Рассмотрим две пространственных области. Одна из них лежит выше плоскости и ограничена верхними частями поверхностей и верхней частью плоскости. Вторая ограничена нижними частями поверхностей и нижней частью плоскости.
В той и другой области поле соленоидально. Следовательно,
, окружающие изолированный источник (сток). Будем считать векторное поле соленоидальным в пространственной области между поверхностями. Рассечем поверхности плоскостью P и выберем на ней «верхнюю» сторону плоскости и «нижнюю» сторону, введем на плоскости вектор нормали от «нижней» стороны к «верхней». Плоскость разделяет поверхности на «верхние» и «нижние» части. Обозначим на них направления внешних нормалей к поверхностям.
Рассмотрим две пространственных области. Одна из них лежит выше плоскости и ограничена верхними частями поверхностей и верхней частью плоскости. Вторая ограничена нижними частями поверхностей и нижней частью плоскости.
В той и другой области поле соленоидально. Следовательно,
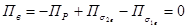 ,
,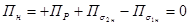 .
.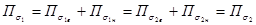 .
.
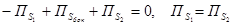 .
.
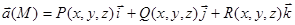 вектор
вектор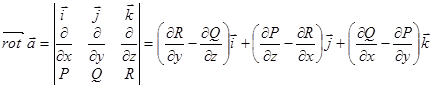
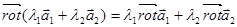
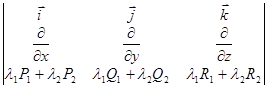 =
= 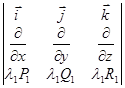 +
+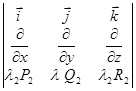 =
= 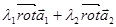 .
.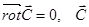 - постоянное векторное поле.
- постоянное векторное поле.
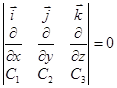
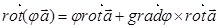
 =
=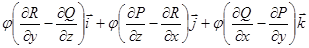 +
+ 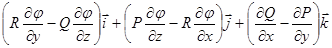 =
= 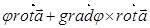 .
. с кусочно-гладкой границей
с кусочно-гладкой границей  .
.

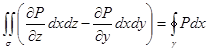 - часть формулы Стокса, в которой содержится только компонента P.
Предположим, что поверхность
- часть формулы Стокса, в которой содержится только компонента P.
Предположим, что поверхность 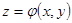 . Тогда нормаль к поверхности
. Тогда нормаль к поверхности

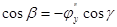 . Вспомним еще, что
. Вспомним еще, что 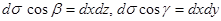 .
.
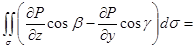
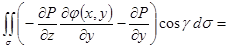
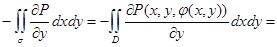
 . Ее можно записать в виде
. Ее можно записать в виде . Нам понадобится только та ее часть, которая относится к функции P
. Нам понадобится только та ее часть, которая относится к функции P 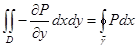 . Продолжаем равенство дальше.
. Продолжаем равенство дальше.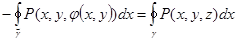 .
.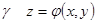 , а переменные x, y на том и другом контуре те же, так как контур
, а переменные x, y на том и другом контуре те же, так как контур 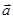 по дуге L называется криволинейный интеграл
по дуге L называется криволинейный интеграл 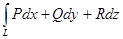 .
.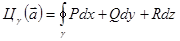 .
.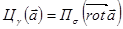 .
.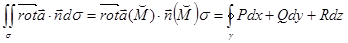 .
.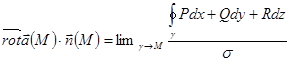
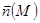 ). Левая часть – это проекция ротора на это направление.
). Левая часть – это проекция ротора на это направление.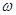
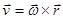 .
.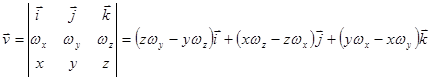 ,
,



