
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лекция 11 Знакоположительные ряды.Содержание книги
Поиск на нашем сайте
Числовой ряд называется знакоположительным, если все его члены – положительные (неотрицательные) числа.
Основная и довольно приятная особенность знакоположительных рядов в том, что частичные суммы ряда представляют собой неубывающую последовательность.
Поэтому достаточно проверить, что последовательность частичных сумм ограничена сверху, чтобы по теореме Вейерштрасса утверждать, что последовательность частичных сумм имеет конечный предел, т.е. ряд сходится. На этом основаны, практически, все признаки сходимости рядов. Ряд может сравниваться с несобственным интегралом (интегральный признак Коши), с другими рядами (признаки сравнения рядов), в частности, со сходящейся геометрической прогрессией (признак Даламбера, радикальный признак Коши). Каждый признак можно сравнить с увеличительным стеклом. У каждого признака есть своя область применения, более широкая или более узкая (как поле зрения линзы) и своя сила. Одни признаки сильнее, позволяют различать слабо сходящиеся или слабо расходящиеся ряды, но имеют узкую область применения (например, интегральный признак Коши). Другие, наоборот, имеют широкую область применения, но довольно слабы, ряды, близкие к границе сходимости, с их помощью не различишь (например, признаки Даламбера и Коши (радикальный)). Пока в библиотеке рядов, которые мы можем использовать для сравнения, всего два ряда: сходящийся ряд - бесконечно убывающая геометрическая прогрессия, известная еще из школы, и расходящийся гармонический ряд, полученный по критерию Коши. Заметим, что критерий Коши (как критерий сходимости), вообще, самый сильный инструмент при исследовании сходимости ряда, но его область применимости узка. Интегральный признак Коши, основанный на сравнении с несобственным интегралом – очень сильный признак. В самом деле, если аппроксимировать непрерывную подинтегральную функцию кусочно-постоянной, то площадь под графиком функции (интеграл) и площадь под графиком кусочно-постоянной функции будут различаться на конечное число.
Интегральный признак Коши.
Доказательство. Так как . Достаточность. Если интеграл сходится, то Необходимость. Если ряд Если ряд расходится, то и интеграл расходится и наоборот. Это легко доказывается от противного. Поэтому говорят, что несобственный интеграл и ряд сходятся или расходятся «одновременно», т.е. один из них сходится, то и другой сходится, если один расходится, то и другой расходится. Это понятие часто употребляют при сравнении рядов.
Пример. Применим интегральный признак к гармоническому ряду.
Пример. Рассмотрим «ряды Дирихле»
Интересно, что ряд Теперь становится яснее, где пролегает граница между сходящимися и расходящимися рядами. Заодно накоплена библиотека сходящихся и расходящихся рядов, которые можно использовать как эталонные при сравнении рядов. Сравнивать ряды можно с помощью признаков сравнения.
Признаки сравнения рядов.
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1816; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.21.12.122 (0.006 с.) |


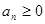

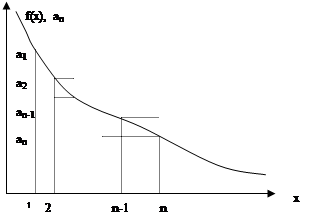






 определена непрерывная, не возрастающая функция f(x), такая, что
определена непрерывная, не возрастающая функция f(x), такая, что  .
Тогда ряд
.
Тогда ряд  .
.
 - это площадь под графиком функции
- это площадь под графиком функции  при
при 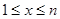 .
. (сумма площадей прямоугольников) ограничивает площадь под графиком функции снизу, а
(сумма площадей прямоугольников) ограничивает площадь под графиком функции снизу, а  ограничивает ее сверху, то
ограничивает ее сверху, то  .
. , поэтому последовательность
, поэтому последовательность  ограничена сверху. Так как эта последовательность не убывает, то по теореме Вейерштрасса
ограничена сверху. Так как эта последовательность не убывает, то по теореме Вейерштрасса  . Поэтому ряд
. Поэтому ряд  при
при  . Поэтому последовательность
. Поэтому последовательность  (неубывающая, так как
(неубывающая, так как  ) ограничена сверху. Следовательно, по теореме Вейерштрасса
) ограничена сверху. Следовательно, по теореме Вейерштрасса  , т.е. несобственный интеграл сходится.
, т.е. несобственный интеграл сходится. - интеграл расходится, поэтому и гармонический ряд расходится.
- интеграл расходится, поэтому и гармонический ряд расходится. . Название взято в кавычки, так неизвестно, рассматривал ли эти ряды Дирихле, но оно устоялось за долгие годы.
. Название взято в кавычки, так неизвестно, рассматривал ли эти ряды Дирихле, но оно устоялось за долгие годы. . Ясно, что интеграл сходится при p>1 и расходится при P<1. Случай p=1 рассмотрен выше (расходящийся гармонический ряд). Отсюда следует вывод
. Ясно, что интеграл сходится при p>1 и расходится при P<1. Случай p=1 рассмотрен выше (расходящийся гармонический ряд). Отсюда следует вывод .
. , интегралы
, интегралы  расходятся (проверьте по интегральному признаку).
расходятся (проверьте по интегральному признаку).


