
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Радиус сходимости и интервал сходимости степенного ряда.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Рассмотрим монотонно убывающую последовательность Такое число Определение радиуса и интервала сходимости степенного ряда. Зафиксируем некоторое значение x и запишем ряд из модулей членов степенного ряда
Применяя признак Даламбера, имеем
Поэтому Применяя радикальный признак Коши, имеем
Так определяется радиус сходимости степенного ряда. Затем исследуется сходимость ряда на границе интервала сходимости, в точках
Пример. Составим ряд из модулей Радиус сходимости R=5, интервал сходимости (-2, 8). Исследуем сходимость ряда на границе, подставляя точки x= -2, в исходный ряд.. В точке x = -2 имеем ряд
В точке x = 8 имеем ряд
Область сходимости исходного ряда (-2, 8].
Теорема. Степенной ряд равномерно сходится внутри интервала сходимости. Доказательство. Пусть где Тогда в области
Следствие. Внутри интервала сходимости справедливы теоремы о непрерывности суммы ряда, о почленном интегрировании и дифференцировании ряда.
Теорема. При почленном дифференцировании и интегрировании степенного ряда его радиус сходимости не меняется.
Доказательство. Рассмотрим ряд из модулей членов степенного ряда (это – знакоположительный числовой ряд в конкретной точке) и определим радиус сходимости по признаку Даламбера.
Продифференцируем почленно степенной ряд
Таким образом, при почленном дифференцировании радиус сходимости степенного ряда не меняется. Он не меняется и при почленном интегрировании, иначе он изменился бы при почленном дифференцировании.
Лекция 15. Ряд Тейлора. Ряд Тейлора.
Рядом Тейлора называется степенной ряд вида Рядом Маклорена называется ряд Тейлора при Теорема. Степенной ряд является рядом Тейлора для своей суммы. Доказательство. Пусть Так как степенной ряд сходится равномерно внутри интервала сходимости, мы можем его дифференцировать почленно. Полученный ряд будет сходиться в том же интервале, так как радиус сходимости при дифференцировании не меняется. Его вновь можно дифференцировать почленно и т.д. Вычислим коэффициенты в степенных рядах, полученных почленным дифференцированием.
Продолжая этот процесс, получим
Следствие. Разложение функции в степенной ряд единственно. Доказательство. По предыдущей теореме коэффициенты разложения функции в степенной ряд определяются однозначно, поэтому разложение функции в степенной ряд единственно.
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 553; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.129.70.138 (0.006 с.) |

 , такую, что в точке
, такую, что в точке  степенной ряд
степенной ряд  расходится. Если выбрать
расходится. Если выбрать  , то степенной ряд будет сходиться (ряд из нулей), поэтому рассматриваемая последовательность ограничена снизу нулем. По теореме Вейерштрасса монотонно убывающая, ограниченная снизу числовая последовательность имеет предел. То есть
, то степенной ряд будет сходиться (ряд из нулей), поэтому рассматриваемая последовательность ограничена снизу нулем. По теореме Вейерштрасса монотонно убывающая, ограниченная снизу числовая последовательность имеет предел. То есть  .
. называется радиусом сходимости степенного ряда. Следовательно, степенной ряд (по теореме Абеля) абсолютно сходится в интервале
называется радиусом сходимости степенного ряда. Следовательно, степенной ряд (по теореме Абеля) абсолютно сходится в интервале  сходимости степенного ряда.
сходимости степенного ряда. . Это – знакоположительный числовой ряд. Применим к нему признак Даламбера или радикальный признак Коши.
. Это – знакоположительный числовой ряд. Применим к нему признак Даламбера или радикальный признак Коши. . Отсюда
. Отсюда  .
.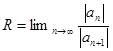 .
. .
. Эти точки подставляются в исходный ряд, ряд становится обычным числовым рядом и исследуется стандартными методами для числовых рядов.
Эти точки подставляются в исходный ряд, ряд становится обычным числовым рядом и исследуется стандартными методами для числовых рядов. .
. , применим радикальный признак Коши
, применим радикальный признак Коши  .
. - гармонический ряд, он расходится.
- гармонический ряд, он расходится. - сходящийся (по признаку Лейбница) знакочередующийся ряд.
- сходящийся (по признаку Лейбница) знакочередующийся ряд. . Выберем
. Выберем  , например
, например 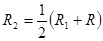 . На интервале
. На интервале  и в точке x1 степенной ряд сходится абсолютно, так как этот интервал лежит внутри интервала сходимости. Тогда (точно так же, как в доказательстве теоремы Абеля оценим
и в точке x1 степенной ряд сходится абсолютно, так как этот интервал лежит внутри интервала сходимости. Тогда (точно так же, как в доказательстве теоремы Абеля оценим 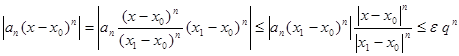 ,
,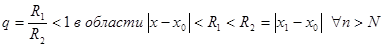 (
(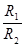 не зависит от
не зависит от 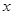 ).
). степенной ряд будет сходиться равномерно по признаку Вейерштрасса (члены ряда мажорируются членами бесконечно убывающей геометрической прогрессии).
степенной ряд будет сходиться равномерно по признаку Вейерштрасса (члены ряда мажорируются членами бесконечно убывающей геометрической прогрессии). .
. , перейдем к ряду из модулей и найдем радиус сходимости по признаку Даламбера.
, перейдем к ряду из модулей и найдем радиус сходимости по признаку Даламбера. .
.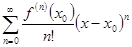 (предполагается, что функция
(предполагается, что функция  является бесконечно дифференцируемой).
является бесконечно дифференцируемой).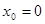 , то есть ряд
, то есть ряд  .
. и степенной ряд сходится в интервале
и степенной ряд сходится в интервале 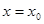 , получим
, получим  .
. =
=  ,
, 
 ,
,  ,
,  ,
, ,
,  ,
,  ,
, . Это – коэффициенты ряда Тейлора. Поэтому степенной ряд есть ряд Тейлора.
. Это – коэффициенты ряда Тейлора. Поэтому степенной ряд есть ряд Тейлора.


