
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
I. Необходимый признак сходимости рядовСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Необходимым признаком сходимости рядов является следующая теорема. Теорема. Если ряд сходится, то предел его общего члена Однако на практике в таком виде применять теорему для исследования ряда невозможно, т.к. мы не знаем, сходится ли наш ряд. Поэтому для практического применения необходимый признак сходимости сформулируем в следующем виде: Следствие. Если предел общего члена ряда при Пример. Исследовать на сходимость ряд Решение. Т.к. Очень важно помнить, что из того, что Замечание. Смысл или польза этого признака: если общий член ряда стремится к нулю, то ряд может быть как сходящимся, так и расходящимся, а если В качестве примера рассмотрим ряд
называемый гармоническим. Необходимый признак сходимости для этого ряда не работает, т.к. Перепишем ряд (2.1) в виде:
Напишем вспомогательный ряд:
Ряд (2.3) строится так, что каждый его член меньше либо равен соответствующему члену ряда (2.2). Обозначим через Т.к. каждый член ряда (2.2) больше либо равен соответствующему ему члену ряда (2.3), то
Вычислим несколько частичных сумм ряда (2.3) для значений
………………………………………………………….
Далее рассмотрим достаточные признаки сходимости знакоположительных рядов. II. Признак Даламбера Теорема. Пусть для ряда а) если б) если в) если Примеры Исследовать следующие ряды на сходимость: 1)
2) Замечание. Напомним, что Решение. Воспользуемся формулой
следовательно, по признаку Даламбера ряд сходится. 3) Решение
и ряд расходится. Замечание. С помощью признака Даламбера исследовать ряды на сходимость имеет смысл только тогда, когда в выражении для III. Радикальный признак Коши Теорема. Пусть для ряда а) если б) если в) если Примеры. Исследовать следующие ряды на сходимость: 1) Решение. Вычислим
2) Решение. Вычислим
Замечание. С помощью радикального признака Коши исследовать ряды на сходимость имеет смысл тогда, когда IV. Интегральный признак Коши Теорема. Пусть члены ряда 1) если несобственный интеграл 2) если несобственный интеграл Для краткости говорят: «Ряд и интеграл ведут себя одинаково». Замечание. Для применения интегрального признака к исследованию сходимости ряда Примеры 1) Применим интегральный признак к исследованию на сходимость ряда вида Решение. В этом случае требуемой функцией является Если Если Следовательно, несобственный интеграл сходится при Запомнить! Обобщенный гармонический ряд 2) Исследовать на сходимость ряд Решение. Выписав Внимание! Пока мы не убедились, что функция невозрастающая на некотором интервале вида Исследуем функцию
V. Признаки сравнения Теорема.Первый признак сравнения (признак сравнения в форме неравенства). Пусть даны два ряда с положительными членами:
причем члены первого ряда не превосходят членов второго при любом
Тогда: а) если сходится ряд (2.6), то сходится и ряд (2.5) б) если расходится ряд (2.5), то расходится и ряд (2.6). Удобно применять другую формулировку этой теоремы: а) если больший ряд сходится, то меньший ряд тоже сходится; б) если меньший ряд расходится, то больший ряд тоже расходится. Примеры Исследовать сходимость следующих рядов: 1) Решение. Сравним данный ряд с гармоническим Понятно, что для применения признака сравнения в форме неравенства нужно сначала установить подходящее неравенство. При этом часто пользуются следующими стандартными неравенствами:
Иногда приходится применять более сложные неравенства:
2) Решение. Прежде всего, заметим, что это ряд с положительными членами, т.к. синус возводится в четную степень. Далее очевидное неравенство 3) Решение. Преобразуем выражение, стоящее под знаком суммы, следующим образом:
(здесь мы учли, что Т.к. ряд Отметим «эталонные» ряды, часто используемые для сравнения: а) геометрический ряд б) обобщенный гармонический ряд Нестандартность применения признака сравнения заключается в том, что надо не только подобрать соответствующий «эталонный» ряд, но и доказать неравенство (2.7), для чего часто требуется преобразование рядов (например, отбрасывание или приписывание конечного числа членов, умножение на определенные числа и т. п.). Более простым оказывается признак сравнения в предельной форме – ведь вычислять пределы обычно гораздо проще, чем доказывать неравенства. Теорема.Второй признак сравнения (признак сравнения в предельной форме). Если Чаще всего исследуемый ряд сравнивают с обобщенным гармоническим рядом Примеры 1) Решение. Сравним данный ряд с обобщенным гармоническим рядом Выпишем предел
Мы пришли к пределу отношения двух степенных выражений на бесконечности. Если степень числителя меньше степени знаменателя, то предел равен 0, а это тот случай, когда признак сравнения в предельной форме не работает. Если степень числителя больше степени знаменателя, то предел равен Разумеется, решение похожих задач не надо расписывать так подробно. Обычно, выписав предел (2.9), далее пишут Следствием второго (предельного) признака сравнения является третий признак сравнения. Теорема.Третий признак сравнения (признак сравнения в форме эквивалентных б.м. или кратко эквивалентный признак сравнения). В общем члене ряда бесконечно малый множитель или делитель можно заменить на эквивалентный, поведение ряда (сходимость или расходимость) от этого не изменится. Замечание 1. Напомним таблицу эквивалентных бесконечно малых величин (при
Замечание 2. При работе с эквивалентным признаком сравнения необходимо помнить, что таблица эквивалентных бесконечно малых величин выписана при 2) Решение. Т.к. при На практике запись ведут кратко:
3) Решение. Т.к. Последний ряд легко исследуется по признаку Даламбера (он сходится). Несмотря на то, что предельный и эквивалентный признаки сравнения более просты по сравнению с признаком сравнения в форме неравенства, иногда без первого признака не обойтись. Покажем это на следующем примере, а заодно продемонстрируем, как надо рассуждать в общем и целом при исследовании рядов на сходимость. 4) Решение. Проверим необходимый признак:
т.е. вопрос о сходимости ряда остается открытым. Этого следовало ожидать (см. замечание к признаку Даламбера). Применим признак сравнения в предельной форме. Сравним данный ряд, например, с гармоническим рядом:
т.е. ответа о сходимости ряда нет. Аналогичная картина наблюдается и при использовании других «эталонных» рядов. Применим, наконец, признак сравнения в форме неравенства (первый признак сравнения). Сравним данный ряд с гармоническим, у которого отброшен первый член: Отметим, что для исследования сходимости данного ряда неприменим и интегральный признак, т.к. первообразная подынтегральной функции не является элементарной функцией, т.е. соответствующий неопределенный интеграл Задачи А) Исследовать ряды с помощью признака Даламбера: 1. 4. B) Исследовать ряды с помощью радикального признака Коши: 7. C) Исследовать ряды с помощью интегрального признака Коши: 11. 14. D) Исследовать ряды с помощью признаков сравнения: 16. 19. Е) Исследовать ряды на сходимость: 22. 25. 28. 31. 34. 37. 40. 43.
|
||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1225; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.108 (0.006 с.) |

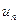 при
при  равен нулю, т.е.
равен нулю, т.е.  .
.
 , то ряд расходится (по необходимому признаку сходимости).
, то ряд расходится (по необходимому признаку сходимости). , не следует ни сходимость, ни расходимость ряда. Говорят, что если
, не следует ни сходимость, ни расходимость ряда. Говорят, что если  , то это заведомо расходящийся ряд. Этот признак является необходимым, но не достаточным.
, то это заведомо расходящийся ряд. Этот признак является необходимым, но не достаточным. , (2.1)
, (2.1) . Докажем, что ряд расходится.
. Докажем, что ряд расходится. (2.2)
(2.2) (2.3)
(2.3) сумму
сумму 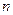 первых членов ряда (2.2), и через
первых членов ряда (2.2), и через  частичную сумму ряда (2.3).
частичную сумму ряда (2.3). . (2.4)
. (2.4) :
:


 следовательно,
следовательно, 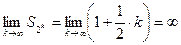 , а тогда в силу (2.4)
, а тогда в силу (2.4)  , и ряд (2.1) расходится.
, и ряд (2.1) расходится.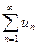 (
(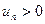 ) существует предел отношения (
) существует предел отношения ( )-го члена ряда к
)-го члена ряда к  . Тогда:
. Тогда: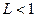 , то ряд сходится,
, то ряд сходится, , то ряд расходится,
, то ряд расходится, , то вопрос о сходимости ряда остается нерешенным, т. е. признак не работает.
, то вопрос о сходимости ряда остается нерешенным, т. е. признак не работает. . Решение. Т.к.
. Решение. Т.к. то по признаку Даламбера ряд сходится.
то по признаку Даламбера ряд сходится.
 , поэтому
, поэтому 
 .
. , тогда:
, тогда:
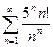


 . Тогда
. Тогда
 , следовательно, по радикальному признаку Коши ряд расходится.
, следовательно, по радикальному признаку Коши ряд расходится.
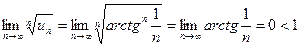 , следовательно, по радикальному признаку Коши ряд сходится.
, следовательно, по радикальному признаку Коши ряд сходится.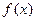 такая непрерывная функция, что
такая непрерывная функция, что 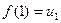 ,
,  , …
, …  , …, причем функция
, …, причем функция 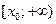 при некотором
при некотором  . Тогда справедливы следующие утверждения:
. Тогда справедливы следующие утверждения: сходится, то сходится и ряд
сходится, то сходится и ряд  , т.е. попросту говоря, выписать
, т.е. попросту говоря, выписать 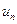 и заменить в нем n на x, и затем исследовать сходимость интеграла
и заменить в нем n на x, и затем исследовать сходимость интеграла  ,
, 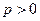 , называемого обобщенным гармоническим рядом или рядом Дирихле.
, называемого обобщенным гармоническим рядом или рядом Дирихле. . Функция
. Функция 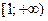 . Вычислим
. Вычислим  .
. , то
, то  .
. , то
, то  .
. и расходится при
и расходится при  . То же самое можно сказать и о данном ряде.
. То же самое можно сказать и о данном ряде. .
.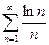 .
. и заменив в нем n на x, получим функцию
и заменив в нем n на x, получим функцию  .
.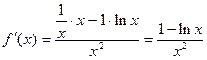 . Критическая точка
. Критическая точка  , на интервале
, на интервале 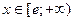
 , т.е. функция
, т.е. функция 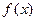 невозрастающая. Теперь можно переходить к интегрированию.
невозрастающая. Теперь можно переходить к интегрированию. ,
,  интеграл расходится, расходится и данный ряд.
интеграл расходится, расходится и данный ряд. (2.5)
(2.5)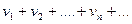 (2.6)
(2.6)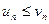 (2.7)
(2.7)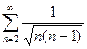
 , мысленно отбросив его первый член, равный 1 (что, естественно, не повлияет на сходимость ряда). Т.к.
, мысленно отбросив его первый член, равный 1 (что, естественно, не повлияет на сходимость ряда). Т.к. 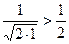 ,
, 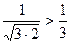 , и вообще,
, и вообще,  (ведь
(ведь 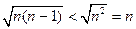 ), то члены данного ряда больше членов расходящегося гармонического ряда, и, следовательно, на основании признака сравнения данный ряд расходится.
), то члены данного ряда больше членов расходящегося гармонического ряда, и, следовательно, на основании признака сравнения данный ряд расходится. , (2.8)
, (2.8) ,
, .
.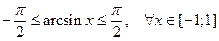 ,
,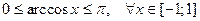 ,
, ,
, ,
, при некотором
при некотором 
 позволяет заключить, что
позволяет заключить, что  , а поскольку ряд
, а поскольку ряд 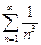 сходится, то и ряд с меньшими членами
сходится, то и ряд с меньшими членами 


 ).
). – сходится (как обобщенный гармонический при
– сходится (как обобщенный гармонический при  – сходится при
– сходится при  , расходится при
, расходится при  ,
, – ряды с положительными членами и существует предел отношения их общих членов
– ряды с положительными членами и существует предел отношения их общих членов 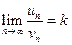 , причем
, причем  , то ряды ведут себя одинаково: либо одновременно сходятся, либо одновременно расходятся.
, то ряды ведут себя одинаково: либо одновременно сходятся, либо одновременно расходятся.
 , причем p подберем в процессе сравнения.
, причем p подберем в процессе сравнения. и преобразуем его:
и преобразуем его: (2.9)
(2.9)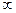 , а это опять тот случай, когда признак сравнения в предельной форме не работает. Таким образом, нас устроит только случай, когда степень числителя равна степени знаменателя, т.е.
, а это опять тот случай, когда признак сравнения в предельной форме не работает. Таким образом, нас устроит только случай, когда степень числителя равна степени знаменателя, т.е.  , или
, или  (в этом случае предел равен отношению старших коэффициентов, т.е. не 0 и не
(в этом случае предел равен отношению старших коэффициентов, т.е. не 0 и не  , т.е. сходится.
, т.е. сходится. ):
): .
. , а в рядах всегда
, а в рядах всегда  , т.е. n является бесконечно большой. А вот бесконечно малыми являются величины вида:
, т.е. n является бесконечно большой. А вот бесконечно малыми являются величины вида: 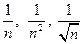 (и вообще
(и вообще  при
при  (и вообще
(и вообще  при
при  ).
).
 (т.е.
(т.е.  – б.м.), то
– б.м.), то  , и ряд
, и ряд  – обобщенный гармонический ряд при p =1/2<1, т.е. расходится.
– обобщенный гармонический ряд при p =1/2<1, т.е. расходится.
 – расходится. Ясно, что слово «расходится» относится к обоим рядам.
– расходится. Ясно, что слово «расходится» относится к обоим рядам.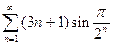 .
. ,то
,то 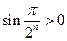 , ряд
, ряд  знакоположительный, и к нему можно применять эквивалентный признак сравнения. Поскольку
знакоположительный, и к нему можно применять эквивалентный признак сравнения. Поскольку  – б.м. при
– б.м. при 

 =
=  .
.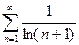
 – необходимый признак не работает. Попробуем применить признак Даламбера:
– необходимый признак не работает. Попробуем применить признак Даламбера: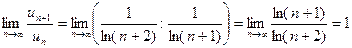 ,
, ,
,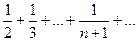 ... Т.к. члены рассматриваемого ряда больше членов расходящегося гармонического
... Т.к. члены рассматриваемого ряда больше членов расходящегося гармонического  , что вытекает из неравенства (2.8), то данный ряд расходится.
, что вытекает из неравенства (2.8), то данный ряд расходится.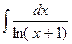 является «не берущимся».
является «не берущимся». 2.
2.  3.
3. 
 5.
5.  6.
6. 
 8.
8.  9.
9.  10.
10. 
 12.
12.  13.
13. 
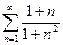 15.
15. 
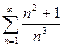 17.
17. 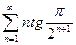 18.
18. 
 20.
20.  21.
21. 
 23.
23.  24.
24. 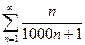
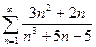 26.
26. 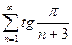 27.
27. 
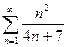 29.
29.  30.
30. 
 32.
32.  33.
33. 
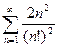 35.
35.  36.
36. 
 38.
38.  39.
39. 
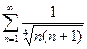 41.
41.  42.
42. 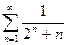
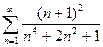 44.
44.  .
.


