
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Эталонные ряды- это ряд, сходимость которого нам известна
Эталонные ряды- это ряд, сходимость которого нам известна Геометрический ряд
Обобщеный гармонический ряд
В частности, при к=1 получаем гармонический ряд
2. Признаки сравнения знакоположительных рядов. Признаки Даламбера и Коши. Предельный признак сравнения рядов. Интегральный признак сходимости рядов. Признаки сравнения знакоположительных рядов. Общий признак сравнения (ОПС). Пусть 1. ряд Q сходится 2. ряд Р расходится { По условию Pn ≤ Qn. (1): Pn ≤ Qn ≤ Q т.е. Pn ограничены и ряд Р сходится (§5). (2): Pn →∞, Qn ≥ Pn Замечание. Неравенство Пример. Исследовать на сходимость: Предельный признак сравнения. Пусть существует 1) С ≠ 0: ряды P и Q сходятся или расходятся одновременно. 2) С = 0: из сходимости Q следует сходимость Р, а из расходимости Р следует расходимость Q. { (1): (2): Предельный признак Коши. Пусть существует Если s < 1 – ряд Р сходится, если s > 1 – расходится. (при s = 1 вопрос о сходимости открыт). {1. сходится. 2. s > 1; Замечание. При использовании признака Коши, полезно помнить: Предельный признак Даламбера.. Пусть существует Если s < 1 – ряд Р сходится, если s > 1 – расходится. (при s = 1 вопрос о сходимости открыт)
Интегральный признак Коши. Пусть функция f (x) ≥ 0 не возрастает при х ≥ 1. В этом случае сходятся или расходятся одновременно. Проинтегрируем эти неравенства от (k – 1) до k и просуммируем по k от 2-х до n: неравенство) и ряд сходится. Если интеграл расходится (к бесконечности!), то частичные суммы неограниченны (правое неравенство) и ряд расходится. В обратную сторону доказательство аналогично.}
3. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимость рядов. Ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков, т. е.: Признак Лейбница — признак сходимости знакочередующегося ряда, установлен Готфридом Лейбницем. Формулировка теоремы:
Пусть для знакочередующегося ряда выполняются следующие условия: 1. 2. Тогда этот ряд сходится. Ряд А называется абсолютно сходящимся, если сходится ряд Если ряд сходится абсолютно, то он сходится. {Обозначим т.е. An = Pn – A*n и ряд А сходится.} Замечание. Отсюда следует, что для абсолютно сходящихся рядов отпадает необходимость в отдельном исследовании на обычную или условную сходимость. Обозначим через pk и qk положительные и модули отрицательных членов ряда А соответственно. Тогда An = Pm – Qs. Ряд А называется условно сходящимся, если он сходится, а ряд A * расходится. Если А сходится абсолютно, то ряды P и Q сходятся. Если А сходится условно, то ряды P и Q расходятся (к бесконечности). {(1): Pn ≤ A* и Qn ≤ A* и ряды P и Q сходятся (§5); (2): предположим, что P, Q сходятся
4. Функциональные ряды. Степенные ряды. Признак равномерной сходимости функционального ряда. Функциональный ряд — ряд, каждым членом которого, в отличие от числового ряда, является не число, а функция Ряд Функциональный ряд называется равномерно сходящимся на множестве D, если
Замечания. 1. Равномерная сходимость рассматривается только на множестве. 2. Наименьшее значение N min, при котором выполняется заключительное неравенство, для каждого
5. Область сходимости степенного ряда. Теорема Абеля. Формула для нахождения радиуса сходимости и ее разновидности. Свойства степенных рядов
Любой степенной ряд сходится в т. х = 0 и S (0) = a 0. Ряд Теорема Абеля. Пусть ряд { Так как ряд Пусть
Признак сходимости коши Если s < 1 – ряд Р сходится, если s > 1 – расходится. (при s = 1 вопрос о сходимости открыт) Формула Тейлора Формула Тейлора используется при доказательстве большого числа теорем в дифференциальном исчислении. Говоря нестрого, формула Тейлора показывает поведение функции вокрестности некоторой точки.Теорема: · Пусть функция · Пусть · Пусть тогда:
БИНОМИАЛЬНЫЙ РЯД - степенной ряд вида
где n - целое, а α - произвольное фиксированное число (вообще говоря, комплексное), z = x + iy - комплексное переменное, (αn) - биномиальные коэффициенты. Для целых α = m ≥ 0 Б. р. сводится к конечной сумме m + 1 слагаемых
8. Разложение функций в ряд Маклорена. Разложение функции Разложение функции f(x) в ряд Тейлора при x0=0
Уравнение кривой, которой описывается форма гибкой нерастяжимой нити, закрепленной концами в двух данных точках, 1) под действием собственного веса; 2) под действием равномерно распределенной нагрузки. Цепной линией называется плоская кривая, форма которой соответствует однородной гибкой нерастяжимой тяжелой нити, закрепленной в обоих концах и провисающей под действием силы тяжести. 1)
Итак, цепная линия описывается гиперболическим косинусом. Ее форма однозначно определяется параметром 2) форма цепной линии равного сопротивления определяется функцией
где b обозначает Формула Грина Пусть в плоскости
25. Криволинейные интегралы первого и второго рода.
Свойства 1. Линейность:
2. Аддитивность: если
3. Монотонность: если
4. Теорема о среднем для непрерывной вдоль
Очевидно, что: 5. Изменение направления обхода кривой интегрирования не влияет на знак интеграла: 6. Криволинейный интеграл первого рода не зависит от параметризации кривой. Вычисление Пусть
Здесь точкой обозначена производная по
Свойства 1. Линейность:
2. Аддитивность:
3. Замечание. Для криволинейных интегралов второго рода несправедливы свойство монотонности, оценка модуля и теорема о среднем.
Вычисление Пусть
Если обозначить за
Формула Стокса
Пусть на ориентируемом многообразии
где Теорема распространяется на линейные комбинации подмногообразий одной размерности, так называемые цепи. В этом случае формула Стокса реализует двойственность междукогомологией де Рама и гомологией циклов многообразия
Дивергенция — след такого тензора производных. Она не зависит от системы координат (является инвариантом преобразований координат, скаляром), а в прямоугольных декартовых координатах вычисляется по формуле:
Это же выражение можно записать с использованием символического оператора набла
Теорема Остроградского-Гаусса позволяет вычислить поток векторного поля с помощью объёмного интеграла от дивергенции поля.
Ротор — векторная характеристика вихревой составляющей векторного поля. Это вектор с координатами:
где i, j и k — единичные орты для осей x, y и z соответственно. Для удобства запоминания можно условно представлять ротор как векторное произведение:
Эталонные ряды- это ряд, сходимость которого нам известна Геометрический ряд
Обобщеный гармонический ряд
В частности, при к=1 получаем гармонический ряд
2. Признаки сравнения знакоположительных рядов. Признаки Даламбера и Коши. Предельный признак сравнения рядов. Интегральный признак сходимости рядов. Признаки сравнения знакоположительных рядов. Общий признак сравнения (ОПС). Пусть 1. ряд Q сходится 2. ряд Р расходится { По условию Pn ≤ Qn. (1): Pn ≤ Qn ≤ Q т.е. Pn ограничены и ряд Р сходится (§5). (2): Pn →∞, Qn ≥ Pn Замечание. Неравенство Пример. Исследовать на сходимость: Предельный признак сравнения. Пусть существует 1) С ≠ 0: ряды P и Q сходятся или расходятся одновременно. 2) С = 0: из сходимости Q следует сходимость Р, а из расходимости Р следует расходимость Q. { (1): (2): Предельный признак Коши. Пусть существует Если s < 1 – ряд Р сходится, если s > 1 – расходится. (при s = 1 вопрос о сходимости открыт). {1. сходится. 2. s > 1; Замечание. При использовании признака Коши, полезно помнить:
Предельный признак Даламбера.. Пусть существует Если s < 1 – ряд Р сходится, если s > 1 – расходится. (при s = 1 вопрос о сходимости открыт)
Интегральный признак Коши. Пусть функция f (x) ≥ 0 не возрастает при х ≥ 1. В этом случае сходятся или расходятся одновременно. Проинтегрируем эти неравенства от (k – 1) до k и просуммируем по k от 2-х до n: неравенство) и ряд сходится. Если интеграл расходится (к бесконечности!), то частичные суммы неограниченны (правое неравенство) и ряд расходится. В обратную сторону доказательство аналогично.}
3. Знакочередующиеся ряды. Признак Лейбница. Абсолютная и условная сходимость рядов. Ряд называется знакочередующимся, если его члены попеременно принимают значения противоположных знаков, т. е.: Признак Лейбница — признак сходимости знакочередующегося ряда, установлен Готфридом Лейбницем. Формулировка теоремы: Пусть для знакочередующегося ряда выполняются следующие условия: 1. 2. Тогда этот ряд сходится. Ряд А называется абсолютно сходящимся, если сходится ряд Если ряд сходится абсолютно, то он сходится. {Обозначим т.е. An = Pn – A*n и ряд А сходится.} Замечание. Отсюда следует, что для абсолютно сходящихся рядов отпадает необходимость в отдельном исследовании на обычную или условную сходимость. Обозначим через pk и qk положительные и модули отрицательных членов ряда А соответственно. Тогда An = Pm – Qs. Ряд А называется условно сходящимся, если он сходится, а ряд A * расходится. Если А сходится абсолютно, то ряды P и Q сходятся. Если А сходится условно, то ряды P и Q расходятся (к бесконечности). {(1): Pn ≤ A* и Qn ≤ A* и ряды P и Q сходятся (§5); (2): предположим, что P, Q сходятся
4. Функциональные ряды. Степенные ряды. Признак равномерной сходимости функционального ряда. Функциональный ряд — ряд, каждым членом которого, в отличие от числового ряда, является не число, а функция Ряд Функциональный ряд называется равномерно сходящимся на множестве D, если
Замечания. 1. Равномерная сходимость рассматривается только на множестве. 2. Наименьшее значение N min, при котором выполняется заключительное неравенство, для каждого
5. Область сходимости степенного ряда. Теорема Абеля. Формула для нахождения радиуса сходимости и ее разновидности. Свойства степенных рядов
Любой степенной ряд сходится в т. х = 0 и S (0) = a 0. Ряд Теорема Абеля. Пусть ряд
{ Так как ряд Пусть
|
|||||||||
|
Последнее изменение этой страницы: 2016-06-23; просмотров: 6825; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.15.214.238 (0.012 с.) |



 − знакоположительные ряды.
− знакоположительные ряды. . В этом случае:
. В этом случае: ряд Р сходится.
ряд Р сходится.
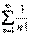 . {
. {  }
} В этом случае:
В этом случае: утверждение следует из ОПС.
утверждение следует из ОПС. и снова ОПС }
и снова ОПС } .
. По ОПС ряд P
По ОПС ряд P ряд Р расходится по необходимому признаку }
ряд Р расходится по необходимому признаку } 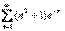

 и
и 

 Если интеграл сходится, то частичные суммы ограничены (левое
Если интеграл сходится, то частичные суммы ограничены (левое
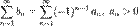
 (монотонное убывание {an})
(монотонное убывание {an}) .
.
 По признаку сравнения ряд Р сходится. Но Pn = An + A * n,
По признаку сравнения ряд Р сходится. Но Pn = An + A * n, , что противоречит условию; пусть теперь Р расходится, а Q сходится. An + Qs = Pm и
, что противоречит условию; пусть теперь Р расходится, а Q сходится. An + Qs = Pm и  что противоречит предположению}
что противоречит предположению} .
. называется степенным рядом. Здесь
называется степенным рядом. Здесь  называют коэффициентами ряда. Любой степенной ряд сходится в т. х = 0 и S (0) = a 0.
называют коэффициентами ряда. Любой степенной ряд сходится в т. х = 0 и S (0) = a 0.
 свое, но, в отличие от обычной сходимости на D, существует наибольшее значение из всех наименьших N:
свое, но, в отличие от обычной сходимости на D, существует наибольшее значение из всех наименьших N:  , которое и фигурирует в определении.
, которое и фигурирует в определении. − степенной ряд с центром в т. х 0.
− степенной ряд с центром в т. х 0. сходится в т.
сходится в т.  Тогда он абсолютно сходится во всех точках х, удовлетворяющих условию
Тогда он абсолютно сходится во всех точках х, удовлетворяющих условию 
 сходится, то
сходится, то  величина
величина  ограничена:
ограничена: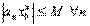 .
. Ряд
Ряд  сходится как бесконечно убывающая геометрическая прогрессия. Следовательно, ряд
сходится как бесконечно убывающая геометрическая прогрессия. Следовательно, ряд  сходится (по признаку сравнения)
сходится (по признаку сравнения) имеет
имеет  производную в некоторой окрестности точки
производную в некоторой окрестности точки  ,
, 

 — произвольное положительное число,
— произвольное положительное число, точка
точка  при
при  или
или  при
при  :
:

 называемой Ньютона биномом.
называемой Ньютона биномом. .
. называется разложением этой функции в ряд Маклорена.
называется разложением этой функции в ряд Маклорена.




 дана ограниченная замкнутым контуром
дана ограниченная замкнутым контуром  правильная область
правильная область  , причем ее проекцией на ось
, причем ее проекцией на ось  является отрезок
является отрезок  , снизу область
, снизу область  , а сверху – кривой
, а сверху – кривой  (в совокупности эти кривые составляют замкнутый контур
(в совокупности эти кривые составляют замкнутый контур  и
и  , имеющие непрерывные частные производные.
, имеющие непрерывные частные производные.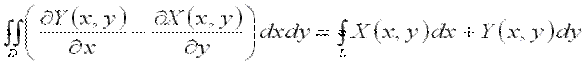 .
.
 в одной точке, то
в одной точке, то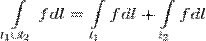
 на
на 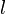 , то
, то
 :
:
 .
. .
.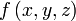 определена и интегрируема вдоль кривой
определена и интегрируема вдоль кривой  .
. :
:  .
.


 ,
, ,
, .
. единичный вектор касательной к кривой
единичный вектор касательной к кривой 


 размерности
размерности  заданы ориентируемое
заданы ориентируемое  и дифференциальная форма
и дифференциальная форма  степени
степени  класса
класса  (
( ). Тогда, если граница подмногообразия
). Тогда, если граница подмногообразия  положительно ориентирована, то
положительно ориентирована, то
 обозначает внешний дифференциал формы
обозначает внешний дифференциал формы 

 ,
,



