
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Необходимый признак сходимости числового ряда.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Гармонический ряд. Нахождение n -й частичной суммы
Теорема. Если ряд
Пусть ряд
Следствие (достаточное условие расходимости ряда) Если
Действительно, если бы ряд сходился, то (по теореме)
Теорема о сходимости дает необходимое условие сходимости ряда, но не достаточное: из условия В качестве примера рассмотрим так называемый гармонический ряд
Очевидно, что Как известно,
т.е. Подставляя в полученное неравенство поочередно n=1, 2, …, n – 1, n, получим:
Сложив почленно эти неравенства, получаем
Достаточные признаки сходимости знакопостоянных рядов.
Необходимый признак сходимости не дает возможности судить о том, сходится ли данный ряд или нет. Сходимость и расходимость ряда во многих случаях можно установить с помощью так называемых достаточных признаков. Рассмотрим некоторые из них для знакоположительных рядов, т.е. рядов с неотрицательными членами.
Признаки сравнения рядов.
Сходимость или расходимость знакоположительного ряда часто устанавливают путем сравнения его с другим рядом, о котором известно, сходится он или нет. В основе такого сравнения лежат следующие теоремы.
Теорема1. Пусть даны два знакоположительных ряда
и
Если для всех n выполняется неравенство
то из сходимости ряда
Обозначим n -е частичные суммы рядов
Пусть ряд Пусть теперь ряд
Теорема2 (предельный признак сравнения) Пусть даны два знакоположительных ряда
По определению предела последовательности для всех n, кроме, возможно, конечного числа их, для любого Если ряд Если ряд Аналогично, если ряд
Признак Даламбера
В отличии от признаков сравнения признак Даламбера позволяет часто решить вопрос о сходимости ряда, проделав лишь некоторые операции над самим рядом.
Теорема Пусть дан ряд Тогда ряд сходится при l<1 и расходится при l>1.
Так как
Пусть l<1. Можно подобрать
т.е. члены ряда Пусть l>1. В этом случае Если l=1, то ряд
Радикальный признак Коши
Теорема. Пусть дан ряд
Как и для признака Даламбера, в случае, когда l=1, вопрос о сходимости ряда остается открытым. Доказательство теоремы аналогично доказательству признака Даламбера.
Интегральный признак Коши
|
||||
|
Последнее изменение этой страницы: 2016-04-23; просмотров: 1715; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.57 (0.007 с.) |

 и ее предела для произвольного ряда во многих случаях является непростой задачей. Поэтому для выяснения сходимости ряда устанавливают специальные признаки сходимости. Первым из них, как правило, является необходимый признак сходимости.
и ее предела для произвольного ряда во многих случаях является непростой задачей. Поэтому для выяснения сходимости ряда устанавливают специальные признаки сходимости. Первым из них, как правило, является необходимый признак сходимости. сходится, то его общий член
сходится, то его общий член  стремится к нулю, т.е.
стремится к нулю, т.е.  .
. . Тогда и
. Тогда и  . Учитывая, что
. Учитывая, что  при n>1, получаем:
при n>1, получаем: .
. или этот предел не существует, то ряд расходится.
или этот предел не существует, то ряд расходится.
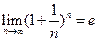 . Отсюда следует, что при любом
. Отсюда следует, что при любом  имеет место неравенство
имеет место неравенство  . Логарифмируя это неравенство по основанию е, получим:
. Логарифмируя это неравенство по основанию е, получим: ,
, ,
, 

 . Поскольку
. Поскольку  , получаем
, получаем  , т.е. гармонический ряд
, т.е. гармонический ряд 

 ,
, и
и  . Из неравенства
. Из неравенства 
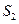 . Тогда
. Тогда  . Члены ряда
. Члены ряда  и, следовательно, с учетом неравенства
и, следовательно, с учетом неравенства  . таким образом, последовательность
. таким образом, последовательность  (
( ) монотонно возрастает (
) монотонно возрастает ( имеет предел
имеет предел  , т.е. ряд
, т.е. ряд  . Тогда с учетом неравенства
. Тогда с учетом неравенства  , т.е. ряд
, т.е. ряд 
 , то ряды сходятся или расходятся одновременно.
, то ряды сходятся или расходятся одновременно. выполняется неравенство
выполняется неравенство  , или
, или  .
. также сходится. Но тогда, согласно свойству1 числовых рядов, ряд
также сходится. Но тогда, согласно свойству1 числовых рядов, ряд  с положительными членами и существует конечный или бесконечный предел
с положительными членами и существует конечный или бесконечный предел  .
. или
или  .
. так, что число
так, что число 
 ,
,  . Обозначим
. Обозначим  , или
, или  . В силу свойства 3 числовых рядов можно считать, что
. В силу свойства 3 числовых рядов можно считать, что 
 меньше соответствующих членов ряда
меньше соответствующих членов ряда  , который сходится как ряд геометрической прогрессии со знаменателем 0<q<1. Но тогда, на основании признака сравнения, сходится ряд
, который сходится как ряд геометрической прогрессии со знаменателем 0<q<1. Но тогда, на основании признака сравнения, сходится ряд  . Отсюда следует, что начиная с некоторого номера N, выполняется неравенство
. Отсюда следует, что начиная с некоторого номера N, выполняется неравенство  , или
, или  , т.е. члены ряда возрастают с увеличением номера n. Поэтому
, т.е. члены ряда возрастают с увеличением номера n. Поэтому  . Тогда ряд сходится при
. Тогда ряд сходится при  и расходится при
и расходится при  .
.


