
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Алгебраические операции и сходимостьСодержание книги
Поиск на нашем сайте
Теорема 4. Пусть Теорема 5. Два сходящихся ряда можно почленно складывать и вычитать, то есть, если ряды
Следствие. Если два ряда
Пример 20. Найдем сумму ряда
Тогда по теореме 5 Теорема 6. Если ряд Пример 21. Рассмотрим ряд Так как Теорема 7. Если оба ряда Пример 22. Рассмотрим ряд Так как
Ряды с неотрицательными членами Критерий сходимости ряда с неотрицательными членами Пусть члены ряда Теорема 8. Для того чтобы ряд с неотрицательными членами сходился, необходимо и достаточно, чтобы последовательность его частичных сумм Если последовательность Пример 24. Исследовать на сходимость ряд Так как
Признаки сравнения Теорема 9 (первый признак сравнения). Пусть даны два ряда:
с неотрицательными членами: Если Пример 25. Исследовать на сходимость ряд
Пример 26. Исследовать на сходимость ряд Пример 27. Исследовать на сходимость ряд При
Пример 28. Ряд Пример 29. Ряд больших n и так как гармонический ряд расходится. Теорема 10 (второй признак сравнения). Пусть даны два ряда:
Теорема 11 (предельный признак сравнения). Если В частности, если Если Пример 30. Исследовать на сходимость ряд Подберем подходящий для сравнения эталонный ряд. Рассмотрим поведение числителя и знаменателя общего члена ряда при
Возьмем
Пример 31. Исследовать на сходимость ряд Преобразуем формулу общего члена ряда:
Пример 32. Ряд
и гармонический ряд расходится. Пример 33. Исследовать на сходимость ряд Так как предел отношения общих членов данного ряда и ряда
предельному признаку сравнения из сходимости ряда Пример 34. Исследовать на сходимость ряд Из асимптотических формул Пример 35. Исследовать на сходимость ряд Так как Признаки Даламбера и Коши Теорема 12 (признак Даламбера). Пусть дан ряд:
Если Если же (Жан Лерон Д`Аламбер (1717-1783) – один из самых разносторонних и влиятельных ученых Франции. Математик, физик, механик, автор физико-математической части «Энциклопедии» Д. Дидро, а также ряда трудов по музыке и эстетике.)
Признак Даламбера часто применяется в предельной форме: если существует верхний предел:
то при В случае Признак Даламбера позволяет дать оценку остатка ряда. Из неравенства
Пример 36. Исследовать сходимость ряда Имеем что Замечание. Из примера следует необходимое условие сходимости ряда, т.е. Пример 37. Ряд
Пример 38. Исследуем на сходимость ряд Имеем
Пример 39. Исследовать сходимость ряда Имеем
Пример 40. Исследовать сходимость ряда По признаку Даламбера:
Окончательная погрешность вычислений (т.е. сумма погрешности от отбрасывания всех членов ряда, начиная с шестого, и погрешности от неточного вычисления пяти членов ряда) будет меньше, чем
Замечание. Для оценки остатка ряда можно было воспользоваться формулой Теорема 13 (радикальный признак Коши). Пусть дан ряд:
Если Если же На практике обычно применяют признак Коши в предельной форме: если существует предел:
то при При Пример 41. Исследуем сходимость ряда Имеем Пример 42. Исследуем сходимость ряда Так как
Пример 43. Исследуем на сходимость ряд Используя асимптотическую формулу Стирлинга
Следовательно, данный ряд расходится.
|
||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 331; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.58.141 (0.007 с.) |

 Ряды
Ряды  и
и  одновременно сходятся или расходятся. Если один из них сходится, то
одновременно сходятся или расходятся. Если один из них сходится, то 
 сходятся, то ряд
сходятся, то ряд  тоже сходится, причем
тоже сходится, причем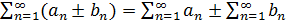 .
. ряд
ряд  также сходится и
также сходится и .
. Данный ряд можно представить как сумму двух рядов:
Данный ряд можно представить как сумму двух рядов:  и
и . Каждый из них является геометрическим рядом со знаменателем
. Каждый из них является геометрическим рядом со знаменателем  , а потому сходится. По формуле (2. 5) суммы первого и второго рядов соответственно равны:
, а потому сходится. По формуле (2. 5) суммы первого и второго рядов соответственно равны:


 и ряд
и ряд  сходится (см. п. 1. 1, пример 14), а гармонический ряд
сходится (см. п. 1. 1, пример 14), а гармонический ряд  расходится, то ряд
расходится, то ряд  расходится.
расходится. .
. то
то 
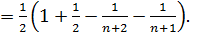 Следовательно,
Следовательно,  т.е. ряд
т.е. ряд  В то же время каждый из рядов
В то же время каждый из рядов  является расходящимся. Расходимость второго ряда очевидна: он получается из гармонического отбрасыванием двух его первых членов.
является расходящимся. Расходимость второго ряда очевидна: он получается из гармонического отбрасыванием двух его первых членов. Последовательность частичных сумм такого ряда является неубывающей. Поэтому по теореме о пределе монотонной последовательности справедливо следующее утверждение.
Последовательность частичных сумм такого ряда является неубывающей. Поэтому по теореме о пределе монотонной последовательности справедливо следующее утверждение. была ограничена сверху:
была ограничена сверху: 

 то
то поэтому ряд сходится.
поэтому ряд сходится.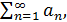 (3.1),
(3.1),
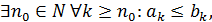 то из сходимости ряда (3.2) с «большими» членами следует сходимость ряда (3.1) c «меньшими» членами, а из расходимости ряда (3.1) следует расходимость ряда (3.2). Ряд (3.2) называют мажорантным для ряда (3.1).
то из сходимости ряда (3.2) с «большими» членами следует сходимость ряда (3.1) c «меньшими» членами, а из расходимости ряда (3.1) следует расходимость ряда (3.2). Ряд (3.2) называют мажорантным для ряда (3.1). Так как
Так как  и ряд
и ряд  сходится (как обобщенный гармонический), то по признаку сравнения исходный ряд сходится.
сходится (как обобщенный гармонический), то по признаку сравнения исходный ряд сходится. Так как
Так как  и гармонический ряд расходится, то данный ряд расходится.
и гармонический ряд расходится, то данный ряд расходится.
 имеем
имеем  Тогда
Тогда Ряд
Ряд  сходится (как обобщенный гармонический), следовательно, по признаку сравнения исходный ряд сходится.
сходится (как обобщенный гармонический), следовательно, по признаку сравнения исходный ряд сходится. сходится, так как
сходится, так как  (для 3> n), и ряд
(для 3> n), и ряд  расходится, так как
расходится, так как 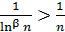 для достаточно
для достаточно Если
Если  то из сходимости ряда
то из сходимости ряда 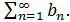
 для всех
для всех  и если
и если  то ряды
то ряды  при
при  , т. е. если
, т. е. если  то ряды
то ряды  то из сходимости ряда
то из сходимости ряда 
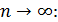
 ,
, .
. и в качестве эталонного ряда рассмотрим обобщенный гармонический ряд
и в качестве эталонного ряда рассмотрим обобщенный гармонический ряд  . Найдем
. Найдем 
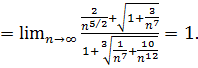 Предел конечен и отличен от нуля, условие предельного признака сравнения выполнено. Эталонный ряд расходится, значит исходный ряд по предельному признаку сравнения тоже расходится.
Предел конечен и отличен от нуля, условие предельного признака сравнения выполнено. Эталонный ряд расходится, значит исходный ряд по предельному признаку сравнения тоже расходится.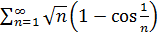 .
. Так как
Так как  при
при  сходится, то и исходный ряд сходится.
сходится, то и исходный ряд сходится. расходится, так как
расходится, так как 


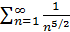 равен нулю:
равен нулю: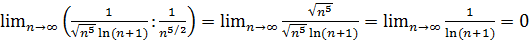 , то по
, то по
 ,
,  при
при 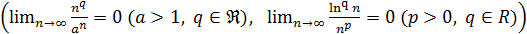 следует, что
следует, что 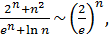 где
где  Так как геометрический ряд
Так как геометрический ряд  сходится, то и данный ряд также сходится.
сходится, то и данный ряд также сходится.
 , то
, то 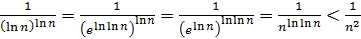 при
при  Из сходимости ряда
Из сходимости ряда 
 то ряд
то ряд  то ряд
то ряд 
 ряд
ряд  - расходится.
- расходится. возможна как сходимость, так и расходимость ряда (требуется провести дополнительное исследование).
возможна как сходимость, так и расходимость ряда (требуется провести дополнительное исследование). следует, что
следует, что  . Отсюда
. Отсюда 

 и т.д. Вообще при любом
и т.д. Вообще при любом  справедливо неравенство
справедливо неравенство  откуда следует, что
откуда следует, что

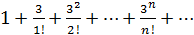
 тогда
тогда  Очевидно,
Очевидно, для
для 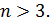 По признаку Даламбера исходный ряд сходится.
По признаку Даламбера исходный ряд сходится.
 сходится, т.к.
сходится, т.к.

 поэтому ряд сходится.
поэтому ряд сходится. .
. Отсюда
Отсюда 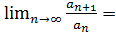
 , т.е. рассматриваемый ряд сходится.
, т.е. рассматриваемый ряд сходится. . Оценить погрешность приближенного равенства
. Оценить погрешность приближенного равенства  Найти в этом случае сумму ряда.
Найти в этом случае сумму ряда. поэтому ряд сходится. Найдем
поэтому ряд сходится. Найдем  . Так как
. Так как то, для того чтобы гарантировать требуемую точность, будем вычислять каждое слагаемое с семью знаками после запятой, делая округление на седьмом знаке. При такой точности вычислений ошибка при подсчете каждого слагаемого будет меньше, чем
то, для того чтобы гарантировать требуемую точность, будем вычислять каждое слагаемое с семью знаками после запятой, делая округление на седьмом знаке. При такой точности вычислений ошибка при подсчете каждого слагаемого будет меньше, чем  и накопление таких ошибок от пяти членов ряда будет меньше, чем
и накопление таких ошибок от пяти членов ряда будет меньше, чем  Поэтому
Поэтому


 где
где 

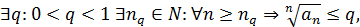 то ряд сходится.
то ряд сходится. то ряд
то ряд 

 , следовательно, по признаку Коши ряд расходится.
, следовательно, по признаку Коши ряд расходится.
 то
то 
 Поэтому данный ряд сходится.
Поэтому данный ряд сходится.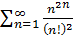 .
. ,
,  получим
получим



