Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие числового ряда и его суммыСодержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Понятие числового ряда и его суммы Основные свойства сходящихся рядов Критерий Коши сходимости ряда
В приведенных примерах п. 1.1 нам удавалось не только установить сходимость или расходимость рассматриваемых рядов, но и найти их суммы (в случае сходимости ряда). Непосредственный анализ последовательности (Коши Огюстен Луи (1789-1857) – французский математик, член Парижской Академии наук.) Теорема 1. Ряд
Если условие (2.1) не выполняется, т.е. если
Определение. Ряд
Из теоремы 1 легко получить следующее важное утверждение. Теорема 2. Ряд Следствие. Прибавление (отбрасывание, изменение) конечного числа членов не влияет на сходимость ряда (но может, конечно, изменить его сумму). Так как для сходящегося ряда Пример 15. Пользуясь критерием Коши, доказать сходимость ряда Пусть
Таким образом, взяв Пример 16. Покажем с помощью критерия Коши, что обобщенный гармонический ряд Для любого
Итак, для Необходимое условие сходимости ряда Из критерия Коши сходимости ряда вытекает Теорема 3. Если ряд члена равен нулю:
Замечание. Как утверждается в теореме, для сходимости ряда необходимо, чтобы Наоборот, если
Для сходимости ряда недостаточно, чтобы n -й член ряда стремился к нулю; нужно, чтобы он стремился к нулю достаточно быстро (обсуждение этого вопроса в п. 3. 2). Пример 17. Рассмотрим ряд
составленный из членов геометрической прогрессии: часто называют геометрическим рядом. Исследуем сходимость данного ряда. Если Пусть Наоборот, если ряд (2. 4) суммируем, то Таким образом, геометрический ряд суммируем тогда и только тогда, когда
Пример 18. Ряд
Пример 19. Ряд
Ряды с неотрицательными членами Критерий сходимости ряда с неотрицательными членами Пусть члены ряда Теорема 8. Для того чтобы ряд с неотрицательными членами сходился, необходимо и достаточно, чтобы последовательность его частичных сумм Если последовательность Пример 24. Исследовать на сходимость ряд Так как
Признаки сравнения Теорема 9 (первый признак сравнения). Пусть даны два ряда:
с неотрицательными членами: Если Пример 25. Исследовать на сходимость ряд Пример 26. Исследовать на сходимость ряд Пример 27. Исследовать на сходимость ряд При
Пример 28. Ряд Пример 29. Ряд больших n и так как гармонический ряд расходится. Теорема 10 (второй признак сравнения). Пусть даны два ряда:
Теорема 11 (предельный признак сравнения). Если В частности, если Если Пример 30. Исследовать на сходимость ряд Подберем подходящий для сравнения эталонный ряд. Рассмотрим поведение числителя и знаменателя общего члена ряда при
Возьмем
Пример 31. Исследовать на сходимость ряд Преобразуем формулу общего члена ряда:
Пример 32. Ряд
и гармонический ряд расходится. Пример 33. Исследовать на сходимость ряд Так как предел отношения общих членов данного ряда и ряда
предельному признаку сравнения из сходимости ряда Пример 34. Исследовать на сходимость ряд Из асимптотических формул Пример 35. Исследовать на сходимость ряд Так как Признаки Даламбера и Коши Теорема 12 (признак Даламбера). Пусть дан ряд:
Если Если же (Жан Лерон Д`Аламбер (1717-1783) – один из самых разносторонних и влиятельных ученых Франции. Математик, физик, механик, автор физико-математической части «Энциклопедии» Д. Дидро, а также ряда трудов по музыке и эстетике.) Признак Даламбера часто применяется в предельной форме: если существует верхний предел:
то при В случае Признак Даламбера позволяет дать оценку остатка ряда. Из неравенства
Пример 36. Исследовать сходимость ряда Имеем что Замечание. Из примера следует необходимое условие сходимости ряда, т.е. Пример 37. Ряд
Пример 38. Исследуем на сходимость ряд Имеем
Пример 39. Исследовать сходимость ряда Имеем
Пример 40. Исследовать сходимость ряда По признаку Даламбера:
Окончательная погрешность вычислений (т.е. сумма погрешности от отбрасывания всех членов ряда, начиная с шестого, и погрешности от неточного вычисления пяти членов ряда) будет меньше, чем
Замечание. Для оценки остатка ряда можно было воспользоваться формулой Теорема 13 (радикальный признак Коши). Пусть дан ряд:
Если Если же На практике обычно применяют признак Коши в предельной форме: если существует предел:
то при При Пример 41. Исследуем сходимость ряда Имеем Пример 42. Исследуем сходимость ряда Так как
Пример 43. Исследуем на сходимость ряд Используя асимптотическую формулу Стирлинга
Следовательно, данный ряд расходится. Знакопеременные ряды Знакопеременный ряд – это ряд, членами которого являются вещественные числа произвольного знака. Определение. Ряд
называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов:
Определение. Сходящийся ряд (2.1) называют условно сходящимся, если ряд (2.2) расходится. Знакочередующиеся ряды Определение. Знакопеременный ряд называют знакочередующимся, если каждые два соседних члена этого ряда имеют противоположные знаки. Обычно знакочередующийся ряд записывают в виде:
Укажем очень простой достаточный признак сходимости знакочередующегося ряда, принадлежащий Лейбницу. (Лейбниц Готфрид Вильгельм(1646–1716) – немецкий математик, физик и изобретатель, юрист, историк, философ-идеалист, языковед.) Теорема (признак Лейбница). Пусть члены знакочередующегося ряда (2.3) удовлетворяют условиям: 1) 2) Тогда ряд (2.3) сходится и для его суммы S справедливо неравенство:
Следствие: Пусть Замечание. Признак Лейбница является следствием признака Дирихле. Пример 59. Исследовать на сходимость ряд Покажем, что ряды, начиная с некоторого номера, убывают по абсолютной величине. Имеем Пример 60. Исследовать на сходимость ряд Рассмотрим ряд, составленный из абсолютных величин членов исходного ряда:
Предел конечен и отличен от нуля, следовательно, ряд Пример 61. Покажем, что ряд Замечание. Для сходимости знакочередующегося ряда выполнение признака Лейбница не является необходимым условием: знакочередующийся ряд может сходиться, даже если модуль его общего члена стремится к нулю не монотонно. Так ряд Пример 62. Исследовать сходимость ряда Так как по правилу Лопиталя
Пример 63. Рассмотрим ряд Ряд только для рядов с неотрицательными членами! Пример 64. Рассмотрим ряд Используя асимптотическую формулу Пример 65. Вычислить приближенно с точностью до
Сходимость ряда следует из признака Лейбница. Так как для сходящегося ряда его сумма
В данном примере
[1] Гармонический ряд – это ряд, каждый член которого, начиная со второго, является средним гармоническим его соседних членов: Понятие числового ряда и его суммы
|
||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 457; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 52.14.140.108 (0.011 с.) |

 не всегда представляется возможным. Так как на практике частичные суммы ряда (в случае его сходимости) принимают за приближенное значение суммы ряда, то представляет интерес выяснение вопроса о сходимости или расходимости числового ряда без вычисления величины его суммы, а также оценка зависимости остатка ряда
не всегда представляется возможным. Так как на практике частичные суммы ряда (в случае его сходимости) принимают за приближенное значение суммы ряда, то представляет интерес выяснение вопроса о сходимости или расходимости числового ряда без вычисления величины его суммы, а также оценка зависимости остатка ряда  от номера n (скорость сходимости ряда). Наиболее общий критерий сходимости числового ряда вытекает из критерия Коши для сходимости последовательности.
от номера n (скорость сходимости ряда). Наиболее общий критерий сходимости числового ряда вытекает из критерия Коши для сходимости последовательности. сходится тогда и только тогда, когда
сходится тогда и только тогда, когда
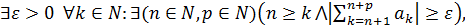 то ряд
то ряд 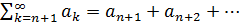 называют остатком ряда
называют остатком ряда 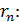
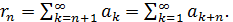
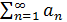 сходится или расходится одновременно с рядом
сходится или расходится одновременно с рядом 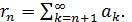 При этом
При этом 
 то при достаточно больших n можно считать, что
то при достаточно больших n можно считать, что 
 .
. – произвольное положительное число. Так как
– произвольное положительное число. Так как то
то 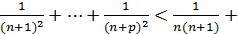
 при произвольном
при произвольном  Отсюда следует, что при
Отсюда следует, что при 
 .
. получим, что при
получим, что при  и произвольном p выполняется требуемое неравенство, и ряд сходится.
и произвольном p выполняется требуемое неравенство, и ряд сходится. расходится.
расходится. возьмем n=k и p=k. Тогда
возьмем n=k и p=k. Тогда
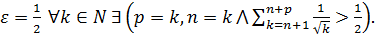 Следовательно, ряд
Следовательно, ряд  (2.3)
(2.3) Таким образом, если
Таким образом, если  то ряд
то ряд  , то ряд не обязательно является сходящимся. Пример гармонического ряда показывает, что это условие не является достаточным: ряд
, то ряд не обязательно является сходящимся. Пример гармонического ряда показывает, что это условие не является достаточным: ряд  расходится, хотя при этом
расходится, хотя при этом .
.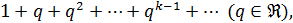 (2.4)
(2.4) Его
Его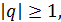 то
то  следовательно,
следовательно,  и в этом случае не выполнен необходимый признак сходимости. Итак, в случае
и в этом случае не выполнен необходимый признак сходимости. Итак, в случае  ряд (2. 4) расходится.
ряд (2. 4) расходится.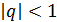 . Тогда
. Тогда 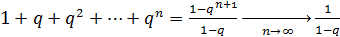 , поскольку
, поскольку 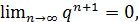 если
если  и, следовательно,
и, следовательно,  . (2.5)
. (2.5)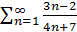 расходится, ибо
расходится, ибо
 расходится, т.к. последовательность
расходится, т.к. последовательность  не является бесконечно малой. В самом деле, предположим противное:
не является бесконечно малой. В самом деле, предположим противное:  . Тогда
. Тогда 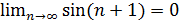 . Так как
. Так как , то
, то  , что противоречит равенству
, что противоречит равенству  . Следовательно, рассматриваемый ряд расходится.
. Следовательно, рассматриваемый ряд расходится. Последовательность частичных сумм такого ряда является неубывающей. Поэтому по теореме о пределе монотонной последовательности справедливо следующее утверждение.
Последовательность частичных сумм такого ряда является неубывающей. Поэтому по теореме о пределе монотонной последовательности справедливо следующее утверждение.

 то
то поэтому ряд сходится.
поэтому ряд сходится.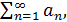 (3.1),
(3.1), (3.2)
(3.2)
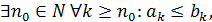 то из сходимости ряда (3.2) с «большими» членами следует сходимость ряда (3.1) c «меньшими» членами, а из расходимости ряда (3.1) следует расходимость ряда (3.2). Ряд (3.2) называют мажорантным для ряда (3.1).
то из сходимости ряда (3.2) с «большими» членами следует сходимость ряда (3.1) c «меньшими» членами, а из расходимости ряда (3.1) следует расходимость ряда (3.2). Ряд (3.2) называют мажорантным для ряда (3.1). Так как
Так как  и ряд
и ряд  Так как
Так как  и гармонический ряд расходится, то данный ряд расходится.
и гармонический ряд расходится, то данный ряд расходится.
 имеем
имеем  Тогда
Тогда Ряд
Ряд  сходится (как обобщенный гармонический), следовательно, по признаку сравнения исходный ряд сходится.
сходится (как обобщенный гармонический), следовательно, по признаку сравнения исходный ряд сходится. сходится, так как
сходится, так как  (для 3> n), и ряд
(для 3> n), и ряд  расходится, так как
расходится, так как 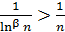 для достаточно
для достаточно Если
Если  то из сходимости ряда
то из сходимости ряда 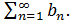
 для всех
для всех  и если
и если  то ряды
то ряды  при
при  , т. е. если
, т. е. если  то ряды
то ряды  то из сходимости ряда
то из сходимости ряда 
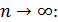
 ,
, .
. и в качестве эталонного ряда рассмотрим обобщенный гармонический ряд
и в качестве эталонного ряда рассмотрим обобщенный гармонический ряд  . Найдем
. Найдем 
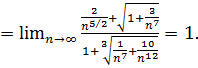 Предел конечен и отличен от нуля, условие предельного признака сравнения выполнено. Эталонный ряд расходится, значит исходный ряд по предельному признаку сравнения тоже расходится.
Предел конечен и отличен от нуля, условие предельного признака сравнения выполнено. Эталонный ряд расходится, значит исходный ряд по предельному признаку сравнения тоже расходится.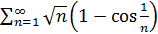 .
. Так как
Так как  при
при  сходится, то и исходный ряд сходится.
сходится, то и исходный ряд сходится. расходится, так как
расходится, так как 


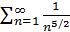 равен нулю:
равен нулю: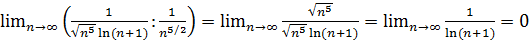 , то по
, то по
 ,
,  при
при 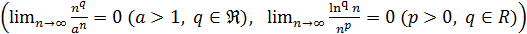 следует, что
следует, что 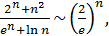 где
где  Так как геометрический ряд
Так как геометрический ряд  сходится, то и данный ряд также сходится.
сходится, то и данный ряд также сходится.
 , то
, то 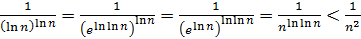 при
при  Из сходимости ряда
Из сходимости ряда 
 то ряд
то ряд  то ряд
то ряд 
 ряд
ряд  - расходится.
- расходится. возможна как сходимость, так и расходимость ряда (требуется провести дополнительное исследование).
возможна как сходимость, так и расходимость ряда (требуется провести дополнительное исследование). следует, что
следует, что  . Отсюда
. Отсюда 

 и т.д. Вообще при любом
и т.д. Вообще при любом  справедливо неравенство
справедливо неравенство  откуда следует, что
откуда следует, что

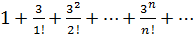
 тогда
тогда  Очевидно,
Очевидно, для
для 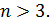 По признаку Даламбера исходный ряд сходится.
По признаку Даламбера исходный ряд сходится.
 сходится, т.к.
сходится, т.к.

 поэтому ряд сходится.
поэтому ряд сходится. .
. Отсюда
Отсюда 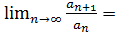
 , т.е. рассматриваемый ряд сходится.
, т.е. рассматриваемый ряд сходится. . Оценить погрешность приближенного равенства
. Оценить погрешность приближенного равенства  Найти в этом случае сумму ряда.
Найти в этом случае сумму ряда. поэтому ряд сходится. Найдем
поэтому ряд сходится. Найдем  . Так как
. Так как то, для того чтобы гарантировать требуемую точность, будем вычислять каждое слагаемое с семью знаками после запятой, делая округление на седьмом знаке. При такой точности вычислений ошибка при подсчете каждого слагаемого будет меньше, чем
то, для того чтобы гарантировать требуемую точность, будем вычислять каждое слагаемое с семью знаками после запятой, делая округление на седьмом знаке. При такой точности вычислений ошибка при подсчете каждого слагаемого будет меньше, чем  и накопление таких ошибок от пяти членов ряда будет меньше, чем
и накопление таких ошибок от пяти членов ряда будет меньше, чем  Поэтому
Поэтому


 где
где 

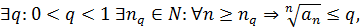 то ряд сходится.
то ряд сходится. то ряд
то ряд 

 , следовательно, по признаку Коши ряд расходится.
, следовательно, по признаку Коши ряд расходится.
 то
то 
 Поэтому данный ряд сходится.
Поэтому данный ряд сходится.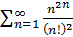 .
. ,
,  получим
получим
 (2.1)
(2.1) (2.2)
(2.2)
 (2.3)
(2.3)

 .
. - остаток ряда (2.3) и пусть выполнены условия 1) и 2) признака Лейбница. Тогда любой остаток ряда не превосходит по абсолютной величине первого из своих членов:
- остаток ряда (2.3) и пусть выполнены условия 1) и 2) признака Лейбница. Тогда любой остаток ряда не превосходит по абсолютной величине первого из своих членов:  ,
,  и имеет одинаковый с ним знак:
и имеет одинаковый с ним знак:  .
. .
. . Так как
. Так как  при
при  , то, начиная с номера
, то, начиная с номера  , выполняется неравенство
, выполняется неравенство  . Кроме того,
. Кроме того,  условия теоремы Лейбница выполнены, следовательно, ряд сходится. Затем, что ряд
условия теоремы Лейбница выполнены, следовательно, ряд сходится. Затем, что ряд  , составленный из модулей членов данного ряда, расходится, так как
, составленный из модулей членов данного ряда, расходится, так как  ,
,  .
. . Сравним его со сходящимся рядом
. Сравним его со сходящимся рядом  .
. расходится. Так как
расходится. Так как  то общий член ряда не стремится к нулю. Необходимое условие сходимости ряда не выполнено, и поэтому исходный ряд расходится.
то общий член ряда не стремится к нулю. Необходимое условие сходимости ряда не выполнено, и поэтому исходный ряд расходится. сходится и притом абсолютно, хотя признак Лейбница и не выполнен: абсолютная величина об-щего члена ряда хотя и стремится к нулю, но не монотонно.
сходится и притом абсолютно, хотя признак Лейбница и не выполнен: абсолютная величина об-щего члена ряда хотя и стремится к нулю, но не монотонно. .
. и
и при
при  то выполнены соответственно условия 1) и 2) признака Лейбница. Поэтому данный ряд сходится. Заметим, что ряд, составленный из абсолютных величин членов данного ряда, расходится:
то выполнены соответственно условия 1) и 2) признака Лейбница. Поэтому данный ряд сходится. Заметим, что ряд, составленный из абсолютных величин членов данного ряда, расходится:  Поэтому ряд
Поэтому ряд  сходится условно.
сходится условно. .
. сходится в силу признака Лейбница, гармонический ряд
сходится в силу признака Лейбница, гармонический ряд  ,
,  где
где  .
. ,
,  получаем
получаем  , где
, где  ,
,  Так как ряд
Так как ряд  в силу признака Лейбница сходится условно, то заданный ряд сходится условно.
в силу признака Лейбница сходится условно, то заданный ряд сходится условно. сумму зна-кочередующегося ряда:
сумму зна-кочередующегося ряда:
 , то при достаточно больших n можно считать, что
, то при достаточно больших n можно считать, что  , причем для остатка ряда справедлива оценка
, причем для остатка ряда справедлива оценка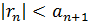 .
. . По условию задачи должно выпол-няться неравенство
. По условию задачи должно выпол-няться неравенство