
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сочетательное свойство для числовых рядов.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Посмотрим, как влияет на сходимость ряда группировка его членов. Пример 54. Сгруппируем формально члены следующего ряда по два, начиная с первого:
Если же формально сгруппировать члены этого же ряда по два, начиная со второго, то получим:
Пример показывает, что группировка членов расходящегося ряда может привести к разным результатам. В общем случае перепишем ряд
где
Обозначим
называют группировкой ряда Теорема 18. Если исходный ряд Замечание. Обратное утверждение неверно. Рассмотрим ряд Теорема 19. Пусть
Тогда ряд Пример 55. Рассмотрим ряд
то рассматриваемый ряд сходится. Поскольку гармонический ряд расходится, то знакопеременный гармонический ряд сходится условно. 4. 1. 2. Переместительное свойство сходящихся рядов Одним из важнейших свойств суммы конечного числа вещественных слагаемых является переместительное свойство. Естественно возникает вопрос, остается ли справедливым это свойство для суммы сходящегося ряда. Определение. Если отображение Пример 56. Рассмотрим условно сходящийся ряд:
Перестать и сгруппируем члены ряда по три следующим образом:
сумма которого равна: Таким образом, перестановка членов условно сходящегося ряда изменяет его сумму. В данном случае она уменьшилась вдвое. Рассмотренный пример показывает, что условно сходящийся ряд не обладает переместительным свойством. Полную ясность в вопрос о сходимости перестановки условно сходящегося ряда вносит следующее утверждение. Теорема 21 (Коши). Если ряд сходится абсолютно, то любая его перестановка также сходится абсолютно, причем к той же сумме. Рассмотрим ряд
Теорема 22 (признак Абеля). Пусть дан ряд (Абель Нильс Хенрик(1802–1829) – норвежский математик, один из крупнейших математиков 19 века.) Теорема 23 (признак Дирихле). Пусть дан ряд (Дирихле Петер Густав Лежён (1805–1859) – немецкий математик.) На практике при применении признаков Абеля и Дирихле в качестве последовательности Пример 57. Пусть последовательность Так как
В частности, например, сходятся ряды:
Пример 58. Рассмотрим ряд Оценка Заметим, что ряд Знакочередующиеся ряды Определение. Знакопеременный ряд называют знакочередующимся, если каждые два соседних члена этого ряда имеют противоположные знаки. Обычно знакочередующийся ряд записывают в виде:
Укажем очень простой достаточный признак сходимости знакочередующегося ряда, принадлежащий Лейбницу. (Лейбниц Готфрид Вильгельм(1646–1716) – немецкий математик, физик и изобретатель, юрист, историк, философ-идеалист, языковед.) Теорема (признак Лейбница). Пусть члены знакочередующегося ряда (2.3) удовлетворяют условиям: 1) 2) Тогда ряд (2.3) сходится и для его суммы S справедливо неравенство:
Следствие: Пусть Замечание. Признак Лейбница является следствием признака Дирихле. Пример 59. Исследовать на сходимость ряд Покажем, что ряды, начиная с некоторого номера, убывают по абсолютной величине. Имеем Пример 60. Исследовать на сходимость ряд Рассмотрим ряд, составленный из абсолютных величин членов исходного ряда:
Предел конечен и отличен от нуля, следовательно, ряд Пример 61. Покажем, что ряд Замечание. Для сходимости знакочередующегося ряда выполнение признака Лейбница не является необходимым условием: знакочередующийся ряд может сходиться, даже если модуль его общего члена стремится к нулю не монотонно. Так ряд Пример 62. Исследовать сходимость ряда Так как по правилу Лопиталя
Пример 63. Рассмотрим ряд Ряд только для рядов с неотрицательными членами! Пример 64. Рассмотрим ряд Используя асимптотическую формулу Пример 65. Вычислить приближенно с точностью до
Сходимость ряда следует из признака Лейбница. Так как для сходящегося ряда его сумма
В данном примере
[1] Гармонический ряд – это ряд, каждый член которого, начиная со второго, является средним гармоническим его соседних членов:
|
||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1041; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.216.202 (0.012 с.) |



 в виде
в виде

 Ряд
Ряд

 сходится, то любая его группировка
сходится, то любая его группировка  также сходится, причем к той же сумме, которую имеет исходный ряд:
также сходится, причем к той же сумме, которую имеет исходный ряд:  .
. . Если
. Если 
 то
то  в то время как исходный ряд
в то время как исходный ряд  а последовательность натуральных чисел
а последовательность натуральных чисел 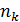 возрастает:
возрастает:

 Этот ряд может быть просуммирован группировкой по два члена:
Этот ряд может быть просуммирован группировкой по два члена:  Так как
Так как
 является биекцией множества N натуральных чисел на себя, то ряд
является биекцией множества N натуральных чисел на себя, то ряд  называется перестановкой ряда
называется перестановкой ряда  .
.
 .
. , общий член которого может быть представлен в виде произведения:
, общий член которого может быть представлен в виде произведения:  . Приведем достаточные признаки сходимости таких рядов.
. Приведем достаточные признаки сходимости таких рядов. . Если последовательность
. Если последовательность  монотонна и ограничена, а ряд
монотонна и ограничена, а ряд  сходится, то ряд
сходится, то ряд  чаще всего берется или последовательность
чаще всего берется или последовательность  , или одна из последовательностей
, или одна из последовательностей  и
и  .
. сходится при любом
сходится при любом  , а ряд
, а ряд  сходится при любом
сходится при любом  .
. ,
,  ,
, то обе суммы ограничены по абсолютной величине числом
то обе суммы ограничены по абсолютной величине числом  . По признаку Дирихле оба ряда сходятся при
. По признаку Дирихле оба ряда сходятся при  ибо все его члены обращаются в нуль.
ибо все его члены обращаются в нуль. ,
,  ,
,  и т.п.
и т.п. .
. не дает информации о поведении ряда
не дает информации о поведении ряда  . Покажем, что исходный ряд сходится. Положим
. Покажем, что исходный ряд сходится. Положим  и
и  . Ряд
. Ряд  монотонна
монотонна  и ограничена
и ограничена  . Поэтому в силу признака Абеля исходный ряд сходится. Расходимость ряда
. Поэтому в силу признака Абеля исходный ряд сходится. Расходимость ряда  и расходимости ряда
и расходимости ряда  . В самом деле, так как
. В самом деле, так как 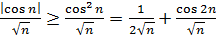 и так как ряд
и так как ряд  сходится, а ряд
сходится, а ряд  расходится, то ряд
расходится, то ряд  расходится. Поэтому в силу теоремы сравнения расходится и ряд
расходится. Поэтому в силу теоремы сравнения расходится и ряд  также сходится условно.
также сходится условно.
 (2.3)
(2.3)


 .
. - остаток ряда (2.3) и пусть выполнены условия 1) и 2) признака Лейбница. Тогда любой остаток ряда не превосходит по абсолютной величине первого из своих членов:
- остаток ряда (2.3) и пусть выполнены условия 1) и 2) признака Лейбница. Тогда любой остаток ряда не превосходит по абсолютной величине первого из своих членов:  ,
,  и имеет одинаковый с ним знак:
и имеет одинаковый с ним знак:  .
. .
. . Так как
. Так как  при
при  , то, начиная с номера
, то, начиная с номера  , выполняется неравенство
, выполняется неравенство  . Кроме того,
. Кроме того,  условия теоремы Лейбница выполнены, следовательно, ряд сходится. Затем, что ряд
условия теоремы Лейбница выполнены, следовательно, ряд сходится. Затем, что ряд  , составленный из модулей членов данного ряда, расходится, так как
, составленный из модулей членов данного ряда, расходится, так как  ,
,  . Поэтому исходный ряд сходится условно.
. Поэтому исходный ряд сходится условно. .
. . Сравним его со сходящимся рядом
. Сравним его со сходящимся рядом  :
: .
. расходится. Так как
расходится. Так как  то общий член ряда не стремится к нулю. Необходимое условие сходимости ряда не выполнено, и поэтому исходный ряд расходится.
то общий член ряда не стремится к нулю. Необходимое условие сходимости ряда не выполнено, и поэтому исходный ряд расходится. сходится и притом абсолютно, хотя признак Лейбница и не выполнен: абсолютная величина об-щего члена ряда хотя и стремится к нулю, но не монотонно.
сходится и притом абсолютно, хотя признак Лейбница и не выполнен: абсолютная величина об-щего члена ряда хотя и стремится к нулю, но не монотонно. .
. и
и при
при  то выполнены соответственно условия 1) и 2) признака Лейбница. Поэтому данный ряд сходится. Заметим, что ряд, составленный из абсолютных величин членов данного ряда, расходится:
то выполнены соответственно условия 1) и 2) признака Лейбница. Поэтому данный ряд сходится. Заметим, что ряд, составленный из абсолютных величин членов данного ряда, расходится:  Поэтому ряд
Поэтому ряд  сходится условно.
сходится условно. .
. сходится в силу признака Лейбница, гармонический ряд
сходится в силу признака Лейбница, гармонический ряд  расходится, следовательно, данный ряд расходится. В тоже время
расходится, следовательно, данный ряд расходится. В тоже время  ,
,  где
где  ,
,  .
. ,
,  получаем
получаем  , где
, где  ,
,  Так как ряд
Так как ряд  в силу признака Лейбница сходится условно, то заданный ряд сходится условно.
в силу признака Лейбница сходится условно, то заданный ряд сходится условно. сумму зна-кочередующегося ряда:
сумму зна-кочередующегося ряда:
 , то при достаточно больших n можно считать, что
, то при достаточно больших n можно считать, что  , причем для остатка ряда справедлива оценка
, причем для остатка ряда справедлива оценка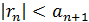 .
. . По условию задачи должно выпол-няться неравенство
. По условию задачи должно выпол-няться неравенство



