Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Пластические и реологические свойства горных пород.Содержание книги
Поиск на нашем сайте
Горные породы, так же как и другие материалы деформируются по-разному при мгновенном и при длительном приложении нагрузки, в результате чего проявляются их различные свойства. Пластичность – явление роста деформаций при некотором возрастании напряжения сверх предела упругости без нарушения сплошности породы. Пластическая деформация в породах обусловлена внутри- и межзеренным скольжением. Внутризеренное скольжение обусловлено дислокациями – сдвигами одной части кристалла относительно другой. К параметрам, характеризующим пластические свойства горной породы, следует относить модуль пластичности (Епл., Па), который представляет собой отношение прироста напряжений в пластической зоне до момента разрушения породы к полной пластической деформации
Параметры
Рисунок 5.4 — График к расчету модуля пластичности образца горной породы.
На графике tga1 равен модулю упругости Е; tga2 – модулю полных деформаций перед разрушением Едеф; tga3 – модулю пластичности Епл; tga4 – модулю спада М несущей способности породы, который характеризует степень хрупкости процесса разрушения породы (поэтому его иначе называют – модуль хрупкости). По величине модуля пластичности можно сравнить относительную пластичность горных пород. Обычно с увеличением предела прочности одноосному сжатию коэффициент пластичности уменьшается. Пластичность зависит от минерального состава горных пород. Наличие жестких кварцевых зерен и полевого шпата в породе уменьшает ее пластичность. Пластичность углей зависит от содержания в них углерода. Модуль упругости более пластичных пород обычно ниже, чем пород менее пластичных. С увеличением числа пластичности глин возрастает их сжимаемость и водонепроницаемость. Пластичность скальных пород увеличивается с повышением температуры и всестороннего давления. Породы, ведущие себя как хрупкие в обычных условиях, при повышенных давлениях и температурах приобретают явно выраженные пластические свойства. Температура ускоряет (интенсифицирует) процесс пластического течения. Пластические деформации при больших всесторонних давлениях объясняются тем, что в этих условиях более легко могут проявиться внутризеренные движения и смещения, не приводящие к нарушению сплошности и к возникновению трещиноватости, т.е. к разрушающим деформациям. Реологические свойства горных пород – свойства, которые характеризуют изменение деформаций и напряжений в горных породах при длительном действии нагрузок. Реологические процессы в горных породах обычно описывают с помощью условно выделенных реологических явлений: ползучесть и релаксация напряжений. На рисунке 5.5 изображен характер проявления ползучести (а) и релаксации (б) в горных породах во времени t.
Рисунок 5.5 — Кривые, характеризующие проявление ползучести и релаксации у твердых тел.
Ползучесть – явление постепенного роста деформаций породы во времени при постоянном напряжении, не превышающем предела упругости. Скорость развития деформаций ползучести на основании теории наследственности часто описывают следующим уравнением
где sτ – напряжения в породе в момент времени τ; t – другой, больший, чем τ момент времени; α и δ – коэффициенты ядра ползучести для данной породы. Они и являются параметрами данного свойства породы; для пород α» 0,7 и δ=(245)10-3. Релаксация напряжений – явление постепенного снижения напряжений в породе при постоянной её деформации. Релаксацию можно представить следующим образом. Если образец горной породы зажать между двумя плоскостями и создать условия, где ε = const, то давление на плоскости со стороны образца в начальный момент будет равно σ, а со временем станет уменьшаться, стремясь к определенной величине. Уравнения кривой релаксации обычно приводят в следующем виде
где to – период релаксации (параметр данного свойства породы), т.е. отрезок времени, за который напряжение снижается в e раз (для горных пород несколько сотен лет, для стекла, например, около 100 лет, а для воды – 10-11 с). Рассмотрение ползучести и релаксации пород показывает, что существует общая закономерность изменения свойств пород со временем действия нагрузки, – чем более длительно воздействие на породу нагрузки, тем слабее становятся упругие свойства пород, уменьшается предел упругости и тем сильнее проявляются её пластические свойства.
В лабораторных условиях реологические параметры горных пород можно определить поперечным изгибом образцов-балочек (рисунок 5.6). Для этих целей используют образцы призматической формы, поперечные размеры которых в 6 – 10 раз меньше его длины. Образцы нагружают постоянной нагрузкой, создающей усилие F.
Рисунок 5.6 – Метод испытания «поперечный изгиб образцов-балочек».
С учетом величин F и t устанавливают величину прогиба уt, а реологические параметры
где уо – величина мгновенного, упругого прогиба, мм.
к – коэффициент влияния касательных напряжений.
h, а, в — соответственно толщина, ширина и длина образца, мм. Обычно измеряют во времени несколько раз величину прогиба (уt) и получают несколько уравнений, которые затем решают как систему линейных уравнений, относительно параметров Весьма характерной чертой реологических процессов, в частности ползучести, является зависимость деформации наблюдаемой в данный момент от характера всего процесса нагружения горной породы, или, другими словами, от всей предыдущей истории его деформирования. Это свойство горных пород называют наследственностью. Теория наследственности была предложена Л. Больцманом с использованием математического аппарата интегральных уравнений В. Вольтерра. Горные породы сохраняют характерную информацию о механических воздействиях в прошлом. Это свойство пород получило название "памяти" о действовавших ранее напряжениях. Со временем (после разгрузки – снятия напряжений) "память" горных пород ослабевает или исчезает полностью. Деформирование горных пород во времени может быть математически опасно путем абстрактного схематического представления горных пород в виде некоторых моделей из структурных элементарных единиц, причем каждая из этих единиц представляет собой упругий, пластичный или вязкий элемент. При этом структурные единицы, обладающие упругими свойствами, могут быть уподоблены пружинами с законом деформирования Гука. Структурные единицы с вязкими свойствами подчиняются закону деформирования Ньютона
где dε/dt – скорость деформирования, η – коэффициент вязкости. В модели они могут быть представлены поршнем со сквозными отверстиями в цилиндре с вязкой жидкостью. Пластические свойства структурных единиц моделируются сухим трением. В этом случае деформирование может иметь место лишь при напряжениях, превышающих некоторое значение, называемое пределом текучести.
Изображение упругих, вязких и пластических элементов при построении реологических моделей горных пород представлено на рисунке 5.7.
Рисунок 5.7 — Изображение упругих (а), вязких (б) и пластических (в) элементов в моделях горных пород.
Деформирование горных пород может быть отражено посредством соответствующего сочетания указанных элементов (рисунок 5.8).
Рисунок 5.8 — Реологические модели горных пород: а – упругого (Гука); б – вязкого (Ньютона); в – упруго-вязкого (Максвелла); д – пластичного (Сен-Венана); е – вязкопластического (Бингама-Шведова), ж – линейного стандартного (Пойнтинга-Томпсона).
Большинство горных пород относится к упрочняющимся телам. Для поддержания в них пластических деформаций необходимо повышать напряжения, рост напряжений происходит с убывающей скоростью. Такое поведение породы моделируется комбинацией идеально упругого тела Гука и идеально вязкого тела Ньютона (поршень с отверстиями, движущийся в цилиндре, наполненном вязкой жидкостью). При параллельном соединении этих тел получается модель тела Кельвина-Фойгта, при последовательном – тела Максвелла. В случае идеального пластического тела после достижения предела упругости тело начинает пластически течь – деформация возрастает при постоянном напряжении. Механическая модель, описывающая эту деформацию, представляет собой тяжелое тело, лежащее на горизонтальной плоскости и соединенное с пружинной (тело Сен-Венана). Комбинируя свойства описанных выше сред, существует модель Бинтама-Шведова, состоящая из последовательно соединенных моделей Сен-Венана и Максвелла. Эта среда при нагрузке, не превосходящей предела текучести, ведет себя как упругая. При нагрузке, превосходящей предел текучести, среда начинает течь, причем напряжения в ней зависят от скорости. Модель стандартной линейной среды описывается моделью Пойтинга – Томпсона. Нагрузка, приложенная к такой модели, вызовет, прежде всего, упругую мгновенную деформацию обеих пружин; в дальнейшем деформация будет расти за счет соответствующего расстояния пружины. Таким образом, все приведенные выше модели можно разделить на классы. Среди них можно выделить класс сред, деформация которых возрастает с течением времени при постоянном напряжении по линейному закону, – модели Максвелла, Сен-Венана, Бингама-Шведова. Возрастание деформаций в таких моделях ограничено только продолжительность действия силы. Другой класс образует модели, деформация которых возрастает по экспериментальному закону, – модели Фойгта, Пойтинга-Томсона и обобщенная линейная среда. Возрастание деформации в таких средах ограничено, предельное значение деформации зависит от величины нагрузки и констант вещества.
Контрольные вопросы
1. Что называется деформацией горной породы? 2. Какие виды деформаций известны? 3. Что называется модулем Юнга, модулем сдвига, коэффициентом Пуассона? 5. Что называется явлением ползучести и релаксации? 5. Какие свойства горных пород называются реологическими? 6. Назовите основные принципы составления реологических моделей.
|
|||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 3091; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.18.59 (0.009 с.) |

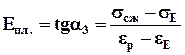 . (5.3)
. (5.3) и
и 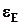 можно определить из графика, представленного на рисунке 5.5.
можно определить из графика, представленного на рисунке 5.5.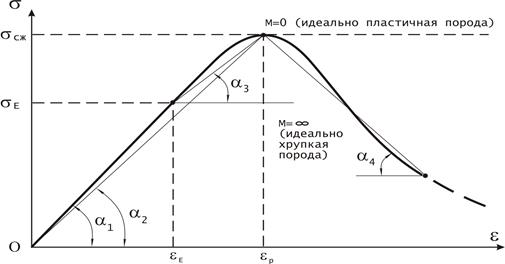

 , (5.4)
, (5.4) , (5.5)
, (5.5)
 и
и  определяют из выражения
определяют из выражения , (5.6)
, (5.6)
 , (5.7)
, (5.7) , (5.8)
, (5.8) , (5.9)
, (5.9)