
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Лабораторные методы исследований
К лабораторным методам исследования механических процессов в породном массиве относятся физическое и аналоговое моделирование. Физическое моделирование предусматривает воссоздание в модели физических полей, действующих в объекте натуры, измененных по своим абсолютным значениям в соответствии с масштабом моделирования. Аналоговое моделирование предусматривает замену в модели по сравнению с натурой одних физических полей другими, например, замену натурного поля механических напряжений электрическим полем в модели. При этом на аналоговых моделях изучают закономерности явлений и процессов, протекающих в натурных объектах, используя математическую аналогию различных по физической природе процессов, т.е. математическую тождественность основных законов, совпадение дифференциальных уравнений, описывающих эти процессы. При ведении горных работ в породном массиве протекают упругие, необратимые пластические деформации, происходят смещения и разрушения пород с разрывом сплошности. Поэтому теоретические расчеты деформирования горных пород, устойчивости горных выработок во многих случаях представляют чрезвычайные трудности. Исследования же в натурных условиях отличаются большой трудоемкостью, дороги и, как правило, требуют длительного времени. Кроме этого в натурных условиях обычно весьма ограничены возможности варьирования отдельными параметрами, тогда как при моделировании можно проследить влияние основных параметров в самых широких пределах. Моделирование открывает также возможности изучения процессов механики горных пород, которые не дают ни аналитические методы, ни наблюдения и измерения в натурных условиях. К физическим методам моделирования относятся моделирование эквивалентными материалами, поляризационно-оптическое и центробежное моделирование. К аналоговому – метод электрогидродинамических аналогий. При физическом моделировании должны выдерживаться геометрическое, кинематическое и динамическое подобие, а также граничные условия. Геометрическое подобие состоит в том, что все размеры пространства, занятого системой в модели, и размеры отдельных элементов модели изменены в определенное число раз по сравнению с соответствующими размерами натурной системы.
Условие кинематического подобия этих систем заключается в том, что любые сходственные точки (частицы) систем, двигаясь по геометрически подобным траекториям, проходят геометрически подобные пути в промежутки времени, отличающиеся постоянным множителем. Условие динамического подобия состоит в том, что массы сходственных частиц этих систем отличаются друг от друга постоянным множителем.
Метод моделирования эквивалентными материалами предложен проф. Г.Н.Кузнецовым с 1936 г. Сущность его заключается в замене горных пород эквивалентными материалами. Моделирование осуществляется на специальных стендах плоских или объемных. В связи с большей трудоемкостью изготовления и отработки объемной модели, а также обработки результатов объемные стенды применяются значительно реже, чем плоские. Размер ребер объемных стендов, применяемых на кафедре горной геомеханики ДонНТУ, равен 0,8-1,0 м. Такие небольшие объемные стенды позволяют решать сравнительно узкий круг задач. Плоские стенды бывают стационарные и поворотные. Последние используются для моделирования угольных месторождений с различными углами падения. При рассмотрении одиночной подготовленной выработки применяются небольшие стенды с размерами 0,8х0,6х0,16 м или 1,2х0,8х0,16 м. При исследовании вопросов, связанных с ведением очистных работ, используются стенды больших размеров 3х2х0,16 м. В ДонУГИ моделируют на стенде с размерами 12х5х0,2 м. Как показал многолетний опыт, результаты, полученные на плоских стендах, не на много отличаются от результатов, полученных при объемном моделировании. В качестве эквивалентного материала используются различные смеси. Исходными инертными материалами могут служить: кварцевый песок, молотая слюда (мика), тальк, мел, глина, известь и др. В качестве вяжущих веществ применяются: гипс, парафин, игдантин, цемент, силикатный клей, вазелин, канифоль и др.
Выбор рецептуры материалов модели зависит от физико-механических свойств моделируемых пород и масштаба моделей.Чаще всего принимается линейный масштаб моделирования 1:50 или 1:100, реже 1:20 или 1:200. При таком масштабе можно смоделировать лишь небольшой участок массива горных пород. Вес вышележащей толщи горных пород в модели заменяется пригрузкой, создаваемой пневмобаллонами (рисунок 15.14).
Прежде, чем приступить к моделированию составляется проект модели. В нем указываются цель и задачи моделирования; мощность и количество слоев, моделирующих различные слои горных пород; расположение отверстий, имитирующих горные выработки, а также методы определения смещений и давления в интересующих точках модели и расположение соответствующих датчиков; порядок отработки модели и обработки результатов моделирования. Исходя из решаемых задач и поведения горных пород в натуре (в шахтных условиях), выбирают тип эквивалентного материала. Так при хрупком характере разрушения породы в натуре можно в качестве вяжущего принять канифоль или гипс, при пластическом – парафин, хрупко-пластическом – канифоль с парафином или игдантином и т.д. Исходя из условий подобия, рассчитываются прочностные и упругие параметры эквивалентного материала для различных типов пород по формуле
где N – предел прочности на сжатие, растяжение, изгиб или модуль Юнга; l – линейный размер, g – плотность; (индекс «М» относится к модели, а «Н» – к натуре). Подобрать эквивалентный материал, который одновременно имел бы все соответствующие параметры, рассчитанные по выше приведенной формуле, практически невозможно. Поэтому определяют тот параметр, который является решающим. Например, при определении нагрузки на одиночную подготовительную выработку определяют предел прочности на сжатие, а при исследовании характера поведения пород кровли в очистном забое – предел прочности на изгиб. Прочность эквивалентного материала зависит от содержания в нем вяжущего. Определение процентного содержания вяжущего в эквивалентном материале осуществляется следующим образом. Закатываются пробные слои с различным содержанием вяжущего, например, гипса от 1 до 15 процентов. При этом количество мела, придающего хрупкость эквивалентному материалу, и воды, смачивающей гипс, во всех слоях принимается одно и то же (4-5%). Остальное количество приходится на мелкий кварцевый песок. После высыхания из каждого пробного слоя изготавливаются образцы эквивалентного материала прямоугольной формы размером 4х2х1 см. Все они поочередно взвешиваются для уточнения gM и испытываются на специальном стенде. Для получения достоверного значения определяемого параметра необходимо испытать не менее пяти образцов. Определяют среднее значение параметра для каждого слоя. По результатам испытаний строят график прочности эквивалентного материала от содержания в нем вяжущего. Для гипсо-песочной смеси характер графика имеет форму, близкую к параболе (рисунок 15.15). При увеличении содержания гипса до 10412% прочность эквивалентного материала возрастает, а при дальнейшем увеличении содержания падает. Это объясняется тем, что принятого количества воды не хватает для смачивания всего гипса. Оставшийся сухой гипс выполняет роль мела, то есть увеличивает хрупкость и снижает прочность эквивалентного материала. Но со временем этот гипс может впитать влагу окружающего воздуха. Это приведет к неконтролируемому увеличению прочности эквивалентного материала. Поэтому при определении процентного содержания гипса в эквивалентном материале, моделирующем различной прочности горные породы, необходимо пользоваться восходящей ветвью графика.
Исходя из размеров стенда, определяют массу одного слоя в модели по формуле
P = lo b×m×gM×k, (15.3)
где lo – длина модели, b – толщина модели; m – мощность слоя; gM – объемная масса материала; k – коэффициент запаса на потери материала при изготовлении, который обычно берется равным 1,1-1,15. После всех подготовительных работ приступают к изготовлению модели из эквивалентных материалов. Закатка материала модели производится слоями мощностью от 6 до 20 мм. Чаще всего 10 мм. При изготовлении модели необходимо иметь весы для взвешивания материала, термометры, смесемешалку с электроподогревом, инструменты и приспособления для приготовления слоев модели (гребенки, катки, трамбовки и т.п.). При применении в качестве вяжущего игдантина песок в смесемешалке нагревается до 80-900. Необходимое для закатки одного слоя количество нагретого песка засыпается в емкость, в него добавляются заранее приготовленные навески вяжущего игдантина и канифоли, которая придает хрупкость. Все это быстро перемешивается и высыпается за опалубку. Во избежание прилипания эквивалентного материала к стенду боковые стороны его и опалубка смазываются глицерином. Наращивание опалубки производится постепенно по мере повышения уровня слоев. Масса материала насыпается по возможности ровным слоем и разрыхляется гребенками. После разравнивания смеси слой укатывается катком. Число укаток, масса катка должны быть такими же, как и при изготовлении пробных слоев. Разделение толщи пород в модели на отдельные слои достигается присыпкой поверхности каждого слоя молотой слюдой. Количество слюды и его крупность создают различные условия трения на контакте между слоями. Воспроизведение трещиноватости (кливажа) в слоях модели осуществляется насечками специальным ножом только что изготовленного слоя. При толще слоев до 10 мм насечки, как правило, не делаются. При использовании в моделях в качестве вяжущего гипса после закатки модель просушивается в течение 25 дней при температуре воздуха в лаборатории 18-200 и относительной влажности 55-65%. Опалубка снимается постепенно за 3-4 приема.
При использовании в качестве вяжущего игдантина или парафина после изготовления модели достаточно 1-2 дней для ее остывания. Опалубка снимается сразу вся. Модель готова к отработке. Отработка модели производится в соответствии с проектом. Проведение выработок, выемка угольного пласта производится путем удаления слоев эквивалентного материала на всю толщу модели. Напряжения в модели создаются весом эквивалентного материала и дополнительным пригрузом, создаваемым рычажными приспособлениями или чаще пневмобаллонами. Наблюдения за поведением модели производятся визуально с описанием внешних признаков деформаций и смещений пород, фотографированием, а также с помощью специальных приборов. Для измерения смещений (сдвижений) пород в модели наиболее широкое применение нашли метод фотофиксации, зеркальные тензометры и реостатные датчики. Сущность метода фотофиксации заключается в том, что поверхность модели с закрепленными в ней реперами систематически фотографируется. Одновременно фотографируются и неподвижные метки, укрепленные на стенде. Измерение смещений точек относительно неподвижных меток производится на стереокомпараторах путем сравнения двух фотопленок, характеризующих начальное и последующее положения реперов при отработке модели. Точность измерения смещений с помощью зеркальных тензометров конструкции Н.М.Зори (ДПИ) значительно выше, чем при фотофиксации, но и трудоемкость этого метода несоизмеримо больше. Как один, так и второй метод не позволяют механизировать измерение смещений в процессе отработки модели, поэтому они вытесняются более прогрессивным методом фиксации смещений с помощью реостатных датчиков. Реостатные датчики крепятся на расстоянии 2-3 см от модели на швеллерах, выдвижные штоки их соединяются с реперами, заложенными в модель (рисунок 15.16). При перемещении репера изменяется сопротивление реостатного датчика. Измерение сопротивления реостатных датчиков также, как и тензодатчиков конструкции ВНИМИ, осуществляется как в ручном, так и автоматическом режимах специальными приборами, например ЦТМ-5. При этом печатающее устройство фиксирует номер и его показание.
Для измерения давления (напряжений) в модели применяют проволочные тензометры конструкции ВНИМИ, датчики из электропроводящей бумаги, датчики трения и т.п. Для перехода от показаний приборов к характеристике давлений в массиве модели производится тарировка приборов. Датчики давления устанавливаются в модели при ее закатке. Тензометр ВНИМИ (рисунок 15.17) состоит из верхней и нижней опорных крышек и средней пластинки из упругого материала с наклеенным на нее проволочным сопротивлением. При прогибе пластинки происходит удлинение проволоки и соответственно изменяется сопротивление. Тензодатчики размещают в таком слое, который обладает той же упругостью, что и датчик. В противном случае происходит разрушение эквивалентного материала.
Датчик из электропроводящей бумаги состоит из двух латунных пластин размером 1х1 см, между которыми находится стопка из 15-20 листов электропроводящей бумаги, выполненной на основе графика. При сдавливании датчика изменяется площадь соприкосновения листов из электропроводящей бумаги и меняется сопротивление датчика.
Датчик трения состоит из двух неподвижных стеклянных пластин, между которыми находится стальная лента. Она передвигается за счет усилий, передаваемых через динамометр. Зная усилие и коэффициент трения металла по стеклу, определяют давление в месте заложения датчика. Такими датчиками выкладывается сплошной слой в модели. Из вышеописанных трех датчиков наиболее точные показания дает тензодатчик конструкции ВНИМИ. Датчики трения в настоящее время применяются ограничено, так как вносят значительные искажения в модель. Кроме того, их показания сильно изменяются при попадании песчинок между стеклом и стальной лентой и при изменении скорости продергивания ленты и т.д. Датчики из электропроводящей бумаги хорошо реагируют на увеличение давления и плохо на его снижение. Поэтому в зонах разгрузки они работают ненадежно. При регистрации смещений с помощью зеркальных тензодатчиков или фотофиксации, а также при измерении давления в модели датчиками трения или из электропроводящей бумаги измерение их показаний в процессе отработки модели и обработку результатов измерений производят вручную. Применение реостатных датчиков для определения смещений и тензодатчиков конструкции ВНИМИ для измерения давления (напряжения) в модели позволяет полностью механизировать как процесс фиксации показаний датчиков, так и обработку результатов измерений. Для этого в память ЭВМ вводятся данные тарировки всех датчиков. В процессе отработки модели результаты измерения сопротивления датчиков автоматическим заносятся в память ЭВМ. По специальной программе производится их обработка. При наличии графопостроителя вычерчиваются по заданным линиям смещения реперов и графики напряжения в модели. Метод моделирования эквивалентными материалами позволяет решать широкий круг задач, связанных с разработкой месторождений полезных ископаемых и управлением состоянием массива горных пород. Он широко применяется во всем мире, не смотря на то, что до сих пор нет единого решения в выборе масштаба времени.
Поляризационно-оптический метод является одним из методов физического моделирования упругого, а иногда и упругопластического и упруговязкого напряженного состояния пород вокруг подземных сооружений. Называют его также методом фотоупругости. Исследования упругих полей напряжений и смещений основываются на использовании закона Гука о прямой пропорциональности между напряжением и деформацией и на явлении оптической анизотропии изотропных тел, подвергнутых воздействию внешних сил или внутренних напряжений. Метод основан на способности большинства прозрачных материалов приобретать свойство двойного лучепреломления при их нагружении. В качестве оптически активных материалов применяют стекло, целлулоид, бакелит и др. Для горных задач нашел применение игдантин (по названию Института горного дела им.А.А.Скочинского), состоящий из фотожелатина (до 55%), глицерина (10-45%) и дистиллированной воды, а также применяются материалы на базе эпоксидных смол различной степени пластификации. Двойное лучепреломление – свойство ряда оптически активных материалов разлагать падающий на них луч света на два луча – обыкновенный и необыкновенный. Первый из них распространяется в материале без преломления, второй преломляется. Обыкновенный и необыкновенный лучи оказываются линейно поляризованными в двух взаимно перпендикулярных плоскостях. В естественном свете колебания совершаются в самых различных направлениях, перпендикулярных к направлению распространения волны. В плоскополяризованном свете колебания светового вектора происходят только в одной плоскости. Если поляризованный луч попадает на напряженную модель из специального прозрачного оптически чувствительного материала, то в результате преломления он распадается на два луча. Колебания этих лучей происходят в плоскостях главных нормальных напряжений. В зависимости от величины разности этих напряжений в модели лучи приобретают разные скорости распространения. Выходя из модели, лучи будут иметь определенную разность хода, т.е. опережение или отставание одной составляющей относительно другой. Поляризационно-оптическая установка – основной прибор, позволяющий изучить распределение напряжений в моделях из оптически активных материалов. Схема поляризационно-оптической установки показана на рисунке 15.18.
Рисунок 15.18 – Схема поляризационно-оптической установки: 1-источник света, 2-поляризатор, 3-модель, 4-анализатор, 5-экран (глаз наблюдателя), 6-отверстие в модели (имитация выработки)
Луч света от источника 1, пройдя через поляроид 2, называемый поляризатором, плоско поляризуется. Поляризованный свет, пройдя далее через напряженную модель 3, претерпевает двойное преломление, которое в разных точках модели зависит от величины и направлений главных напряжений в этих точках. Далее оба луча, образовавшиеся в рассматриваемой точке модели в результате двойного лучепреломления, проходят через поляроид 4, называемый анализатором, и при этом их колебания приводятся в одну плоскость. Прошедшие анализатор плоскополяризованные лучи интерферируют, т.е. дают интерференционную картину на экране. В результате полученной интерференции наблюдается цветная картина полос при белом источнике света и черно-белая – при монохроматическом (с одной длиной волны). При этом каждая цветная полоса представляет собой геометрическое место точек с одинаковой оптической разностью хода и, следовательно, с одной и той же разностью главных нормальных напряжений. Таким образом, цветные полосы на экране представляют собой линии равных максимальных касательных напряжений исследуемой модели. Эти линии называются изохромами. Картину изохром, получаемую в поле анализатора, можно наблюдать визуально и фотографировать. Для оптического метода должно быть соблюдено геометрическое и механическое подобие. Геометрическое подобие обеспечивается тем, что все линейные размеры модели выполняются в одном масштабе относительно размеров натуры. Механическое подобие модели и натуры обеспечивается подбором свойств материала и граничных условий нагружения. Зависимость оптической разности хода и разности главных напряжений в рассматриваемой точке модели имеет вид
Г = Сd (s1 - s2), (15.4) где Г – оптическая разность хода, м; С – коэффициент оптической чувствительности материала по напряжению, 1/Па; d – толщина модели, м; s1, s2 – главные нормальные напряжения в модели, Па. Вышеприведенная формула выражает основной закон фотоупругости. Она устанавливает количественную взаимосвязь между напряжениями в модели и вызываемым им оптическим эффектом. Из теории упругости известно, что полуразность главных нормальных напряжений равна максимальному касательному напряжению tmax, т.е.
Отсюда следует, что
Разность хода может быть определена по методу сопоставления цветов, по методу полос и по методу компенсации. Наиболее простым и достаточно точным методом является метод полос. При монохроматическом свете в точках, для которых
Г = 2ml/2, (15.7)
где l – длина волны света, m – целое число, характеризующее порядок полосы, который надо определить (счет полос ведется от крайней внешней полосы, для которой m = 0), наблюдается погашение света – минимум. В точках, где
Г = (2m+1)
наблюдается максимальная освещенность – максимум. Условие максимума при белом свете остается прежним. Поляризационно-оптический метод отличается простотой и наглядностью. Так как без всяких расчетов показывает место концентрации касательных напряжений (место, в котором наибольшее количество изохром) и место, в котором прежде всего следует ожидать разрушения материала. Метод позволяет решать плоские, в основном упругие задачи. Поэтому в горном деле применяется для решения ограниченного круга задач, например, исследование влияния формы и размеров поперечного сечения подготовительной выработки на характер распределения касательных напряжений на ее контуре в однородной изотропной среде (горных породах); влияния щелевой разгрузки на характер распределения касательных напряжений вокруг выработки и т.д. Широкое распространение метод получил в горном машиностроении.
Метод центробежного моделирования состоит в том, что модель из горных пород моделируемого объекта, выполненную в заданном геометрическом масштабе, помещают в каретку центрифуги (рисунок 15.19) и путем равномерного вращения нагружают объемными инерционными силами, придавая тем самым породам модели некоторый фиктивный объемный вес. Исходя из решаемой задачи, определяют масштаб моделирования, который показывает во сколько раз во вращающейся модели увеличен объемный вес пород, и представляет собой величину, обратную геометрическому масштабу модели, а также рассчитывают необходимое число оборотов центрифуги в минуту. При решении задач механики горных пород с применением центробежного моделирования обычно испытывают от 2 до 6 идентичных моделей (моделей-близнецов), помещая их попарно в каретки центрифуги. Измерения в модели ведут путем фиксации различных параметров до и после испытания модели в центрифуге, а также в процессе вращения. Для измерения напряжений в различных точках модели используют аэростатические динамометры, тензометрические датчики рамного и мембранного типа. Для измерения неупругих деформаций применяют сельсиновые пары, индикаторы часового типа, индукционные датчики и др. Все эти датчики используют в системе, позволяющей вести непрерывную дистанционную регистрацию их показаний на пульте управления центрифугой.
Современные центрифуги позволяют испытывать модели высотой до 0,4-0,5 м. В зависимости от решаемых задач масштаб центробежного моделирования n находится в пределах от 20 до 500. В частности, центрифуга Криворожского НИГРИ имеет следующие параметры: наружный диаметр 6 м, эффективный радиус 2,5 м, максимальная скорость вращения 425 об/мин, размер кареток 1,5х0,8х0,6 м, мощность привода 650 кВт. Установка изготовлена из особо прочных титановых сплавов. Метод центробежного моделирования с успехом и большой степенью надежности применяют при решении задач, связанных с определением размеров устойчивых потолочин камер, оптимальной формы и параметров бортов карьеров и отвалов, давления обрушенных пород на днища очистных блоков, влияния длительной нагрузки на крепь капитальных выработок, пройденных в пластичных глинистых горных породах и др. Использование специальных устройств позволяет моделировать в центрифуге одновременное действие статического поля напряжений и динамического поля, создаваемого при взрывных работах. Вместе с тем метод центробежного моделирования имеет ряд ограничений. Одно из них состоит в том, что центробежное моделирование в связи с изменением эффективного радиуса вращения не обеспечивает в модели однородности механического силового поля. Размеры моделей ограничены размерами кареток. При центробежном моделировании крайне затруднительно или даже невозможно воспроизводить слоистые толщи разнородных по составу и свойствам пород. Большие технические трудности представляет воспроизведение в модели перемещения забоя во времени. Все это ограничивает область эффективного применения данного метода.
Среди других методов заслуживают внимания электроаналогивые методы моделирования, т.е. электрическое моделирование физических полей. Эти методы основаны на совпадении дифференциальных уравнений, описывающих процессы в электрическом и механическом силовых полях. Электрические модели бывают двух типов. В одном из них – методе электродинамических аналогий (ЭГДА), предложенном в 1922 г. акад. Н.Н.Павловским, используют меняющиеся электрические свойства сплошной проводящей среды. Другой, известный под названием метода электрических сеток прямой аналогии (ЭСПА), предусматривает замену сплошной среды сеткой из некоторых элементарных электрических ячеек, параметры которых назначают исходя из свойств среды в механической системе и критериев подобия. При применении метода ЭГДА на электропроводной бумаге в определенном геометрическом масштабе и с соблюдением граничных условий строится модель. Для этого на шины-зажимы, прикрепленные к месту электропроводной бумаги, с потенциометрических делителей напряжения подается напряжение различной величины. Изменяя величину подаваемого на отдельные шины напряжения, моделируют различный характер распределения напряжений в плоскости отрабатываемого пласта, например, эпюру опорного давления. Используя аналогию между распределением напряжений в породном массиве при очистной выемке и стационарным движением тока в электропроводящей среде, по распределению потенциала на листе электропроводной бумаги устанавливают характер распределения напряжений в почве отрабатываемого пласта. Таким образом, метод ЭГДА позволяет изучить параметры зон опорного давления и разгрузки в почве отрабатываемого пласта, закономерность их изменения в зависимости от глубины разработки, размеров оставляемых целиков угля, выработанного пространства и т.д. Эти данные используются при выборе места расположения полевых выработок, а также при решении других горных задач, связанных с управлением состоянием массива горных пород и обеспечением устойчивости горных выработок. Отмечается, что в настоящее время электроаналоговые методы применяются для решения задач, связанных с динамическими процессами в породных массивах. Однако дальнейшее развитие этих методов может открыть пути моделирования совместного действия статических и динамических процессов механики горных пород. Наряду с выше описанными методами при решении задач механики горных пород используются также методы, представляющие собой комбинации двух принципов моделирования, например, центробежного моделирования и поляризационно-оптического метода или метода эквивалентных материалов и центробежного моделирования. Так, например, при использовании оптической установки, описанной ранее, могут использоваться только плоские модели. Объемные модели из оптически чувствительных материалов изучают с использованием центрифуги. При этом объемные силы (вес горных пород) заменяются центробежными силами. В этом случае сочетаются принципы оптического моделирования и методы центробежного моделирования. В заключение следует отметить, что из всех выше рассмотренных методов моделирования наибольшее распространение в горном деле получил метод эквивалентных материалов. Аналитические исследования
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 631; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.145.88.130 (0.09 с.) |

 , (15.2)
, (15.2)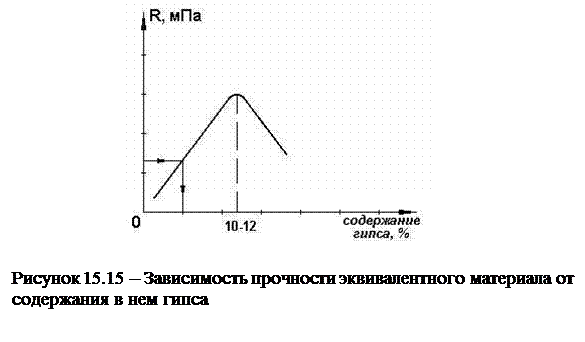



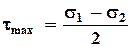 (15.5)
(15.5)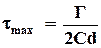 (15.6)
(15.6) (15.8)
(15.8)



