Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Понятие о напряжениях и деформацияхСодержание книги
Поиск на нашем сайте
Рассмотрим на простейшем виде деформации – разбежные – элементарные внутренние усилия и перемещения, возникающие при действии на брус продольной силы F (рисунок 4.1). Разрезаем мысленно брус сечением на две части, действие одной части на другую заменяем усилием N (продольная сила). Эта продольная сила определяется из уравнения статики
Рисунок 4.1 – К расчету бруса при растяжении
Продольная сила является равнодействующей элементарных сил, определяющих взаимодействие между частицами тела. При растяжении естественно предположить, что элементарные силы равномерно распределяются по площади сечения и называются напряжением. Напряжения – мера интенсивности внутренних сил. При растяжении возникают нормальные напряжения (перпендикулярно к сечению) σ, которые определяются по формуле
где N – продольная сила, Н; S – площадь поперечного сечения, м2. Обычно принимают следующее правило знаков: - если нормальное напряжение (сила) направлено от сечения, оно вызывает растяжение и считается положительным; - если нормальное напряжение (сила) направлена к сечению, то оно вызывает сжатие и считается отрицательным. Между этими видами деформаций сохраняется единство при анализе внутренних сил, но и обнаруживаются качественные отличия, например, при изучении процессов разрушения материалов или при исследовании поведения длинных и тонких стержней, для которых сжатие сопровождается изгибом. Условие прочности: напряжение, возникающее в опасной точке конструкции, среды, должны быть меньше или, по крайней мере, равны допускаемым напряжениям
Допускаемые напряжения определяют по зависимости
где σпред – предельное напряжение, определяемое в результате испытаний образцов при различных условиях нарушения; n – коэффициент запаса прочности, n > 1. Под действием приложенных сил брус изменяет свои размеры (рисунок 4.2). До деформации длина его была ℓ после деформации ℓ1 = ℓ + ∆ℓ. Величина ∆ℓ называется абсолютным удлинением бруса. Отношение
называют относительным удлинением бруса. Но правильное название – линейная деформация, иногда продольная деформация.
Рисунок 4.2 – Изменение размеров бруса
В поперечном направлении произошло уменьшение поперечного размера и поперечная деформация равна
Между поперечной и продольной деформацией существует зависимость. Отношение поперечной деформации к продольной носит название коэффициента Пуассона и является механической характеристикой материала и определяется экспериментальным путем.
В пределах малых удлинений для подавляющего большинства материалов, в том числе и для горных пород, справедлив закон Гука, который устанавливает пропорциональную зависимость между напряжениями и деформациями:
где Е – модуль упругости первого рода или модуль упругости, МПа. Эта величина является физической константой материала и определяется экспериментально. Определим напряжения, возникающие в брусе при растяжении в некотором сечении, нормаль к которому расположена под углом α к оси бруса (рисунок 4.3, а).
Рисунок 4.3 – Напряжения в наклонных площадках
Напряжения р равномерно распределены по наклонному сечению и их можно определить из условия равновесия правой части бруса
где А – площадь поперечного сечения бруса; Аα – площадь наклонного сечения бруса. Таким образом, напряжение в наклонном сечении
Обычно это напряжение раскладывали на два направления: по нормали к сечению, нормальное напряжение σα и вдоль площадки – касательное напряжение τα (рисунок 4.3, в) и они равны
Как видно из уравнений, в зависимости от организации сечения получаем разные по величине и направлению нормальные и касательные напряжения. В сечениях при α = 0, σα = σ, τα; в сечениях α = 900, σα = 0, τα = 0; в сечениях при α = 450, возникают наибольшие касательные напряжения Как видно на примере растяжения бруса, напряжения в площадке (сечении) зависят от ее ориентации. Через данную точку в конструкции, в массиве горных пород, можно провести бесчисленное множество сечений, в которых действуют различные по величине и по направлению нормальные и касательные напряжения, которые отражают взаимодействие бесконечного множества частиц на данную точку. Напряжения, действующие по любым трем взаимно перпендикулярным площадкам определяют напряженное состояние в точке. Условно напряженное состояние в точке представляют следующим образом: вокруг точки вырезаем элемент бесконечно малого размера в форме параллелепипеда (рисунок 4.4, а). При уменьшении сторон, в пределе (dx, dy, dz → 0) этот параллелепипед стягивается в точку, через которую проходят три взаимно перпендикулярные площадки. По граням элемента могут действовать напряжения Рх, Ру, Рz (рисунок 4.4, а). Раскладываем эти напряжения на составляющие, проецируют их на оси х, у, z, получаем нормальные напряжения σх, σу, σz и касательные напряжения τху, τух, τуz, τzy, τzx, τxz. Индекс нормального напряжения соответствует нормали к площадке, на которой они действуют. Касательные напряжения имеют два индекса: первый – направление оси, параллельной напряжению, второй – направлению оси, перпендикулярной к площадке. Таким образом, на гранях элементарного параллелепипеда действуют девять компонент напряжений, которые представляют собой тензор напряжений, записываемый в виде
где в строках расположены составляющие напряжений соответственно на площадках, перпендикулярных осям х, у, z.
Рисунок 4.4 – Напряженное состояние в точке
Система сил, приложенных к элементу, должна удовлетворять условиям равновесия. Поскольку на противоположных гранях возникают противоположные по направлению силы, то первые три условия равновесия – для пространственной системы сил. Из условия равновесия суммы моментов относительно оси х, получаем
аналогично можно записывать остальные уравнения. Тогда получаем
Таким образом, на двух взаимно перпендикулярных площадках составляющие касательных напряжений, перпендикулярные к общему ребру, равны и направлены обе либо к ребру, либо от ребра. Это есть закон парности касательных напряжений. Следовательно, на гранях выделенного элемента имеем не девять, а шесть независимых компонент напряжений, поскольку касательные напряжения попарно равны. Тензор напряжений (4.8) является симметричным. Анализ напряженного состояния в точке начинается всегда с определения напряжений на гранях выделенного в окружности точки элемента. Через точку проводится три взаимно перпендикулярные плоскости, ориентация которых может быть произвольной и часто определяется более простым расчетом компонент напряжений. Например, напряжение в толще горной породы определяем следующим образом. Выбираем некоторую точку, положение которой определяем с помощью прямоугольной системы координат, началом которой считают точку на границе действия внешних сил и горной породы. Ось z направлена вниз, ось у – слева направо, ось х – перпендикулярно к оси у (рисунок 4.5, а).
Рисунок 4.5 – Напряженное состояние в точке б толще горной породы
Для оценки сжимаемости горной породы под действием внешней нагрузки обычно рассматривают горизонтальные и вертикальные площадки. В таком случае решение задачи о сжатии горной породы в некоторой точке сводится к решению о сжатии заменяющего эту точку элементарного параллелепипеда, стороны которого параллельны оси координат, что допустимо в силу его малости. Напряжения в породах могут создаваться не только действием внешних нагрузок, но и другими физическими полями. Например, термические напряжения вызываются неоднородным нагревом пород. При изменении ориентации граней выделенного элемента или, иначе, при проведении различных площадок через данную точку изменяются напряжения, действующие по этим граням. Среди бесчисленного множества площадок, проходящих через данную точку, имеется три взаимно перпендикулярных площадки, на которых касательные напряжения равны нулю. Такие площадки называются главными площадками, а нормальные напряжения на этих площадках – главными напряжениями. Главные напряжения обозначаются σ1, σ2, σ3 в порядке убывания в алгебраическом смысле, т.е. σ1 > σ2 > σ4. Если по всем трем граням параллелепипеда действует три напряжения, то напряженное состояние называется объемным или трехосным (рисунок 4.6, а). Если на гранях элемента действуют два напряжения σ1, σ2, то напряженное состояние называется плоским или двухосным (рис. 4.6, б). Если на гранях элемента действуют напряжения σ1, то напряженное состояние называется линейным или одноосным (рис. 4.6, в).
Рисунок 4.6 – Виды напряженных состояний
В дальнейшем при исследовании напряженного состояния в точке необходимо определять главные напряжения, потому что расчеты на прочность построены на основании главных напряжений. Рассмотрим напряжения, возникающие в наклонных площадках при плоском напряженном состоянии. По граням элемента действуют главные напряжения σ1 и σ2. Определяем напряжения на площадке, нормаль к которой составляет угол α с горизонтальной осью (рисунок 4.7). На рисунке 4.7 представлена проекция параллелепипеда. Применяем принцип независимости действия сил (принцип суперпозиций) и на основании формул (4.7) определяем нормальные и касательные напряжения.
Рисунок 4.7 – Плоское напряженное состояние
окончательно получаем
После преобразований можно записать
Эти зависимости представляют уравнение окружности в параметрической форме в системе координат σ и τ. Таким образом, напряженное состояние в точке можно представить графически в виде окружности, координаты точек которой определяют напряжения на соответствующей площадке, а угол α определяет ориентацию площадки. Центр окружности находится на расстоянии
В системе координат σ1, τ точка В соответствует вертикальной площадке, точка С – горизонтальной площадке (рисунок 4.8).
Рисунок 4.8 – Круговая диаграмма напряженного состояния
Точка А соответствует площадке, нормаль к которой расположена под углом α к горизонтали. Для определения направления напряжений σα и τα находим на круге напряжений полюс круга, точку, где пересекаются все нормали к площадкам. Находим полюс следующим образом, в точке В нормаль к площадке – горизонтальная линия, в точке С нормаль к площадке – вертикальная линия, они пересекаются в точке С, эта точка и является полюсом. Соединив точки А и С прямой, получим направление напряжения σα и соответственно τα (рис. 4.8).
Рисунок 4.9 – Круговая диаграмма напряженного состояния
Главным площадкам соответствуют точки К и М, в этих площадках действуют наибольшие и наименьшие напряжения. Наибольшие и наименьшие напряжения равны
После подстановки отрезков получаем
затем обозначаем напряжения согласно принятой зависимости σ1 > σ2 > σ4. Направление главных напряжений определяется на основании зависимости
Наибольшие касательные напряжения численно равны радиусу окружности напряжений
При испытании образцов пород на прочность при растяжении, сжатии получаем линейное напряженное состояние. Круговые диаграммы напряженных состояний представлены на рисунке 4.10. Рассмотрим построение диаграммы напряжений для объемного напряженного состояния. Для площадок параллельных осям х, у, z строим круги Мора (рисунок 4.11).Каждой точке любой окружности соответствует определенная площадка. Однако, точки, расположенные на трех кругах не исчерпывают всего множества площадок, проходящих через заданную точку. Точки, соответствующие площадкам, не параллельным ни одной из главных осей, расположены внутри заштрихованного криволинейного треугольника АВС, образованного тремя совмещенными кругами Мора (рисунок 4.12).
Рисунок 4.10 – Круговая диаграмма напряженного состояния при растяжении (а) и при сжатии (б)
Наибольшие касательные напряжения равны радиусу наибольшего круга
Рисунок 4.11 – Круговые диаграммы для объемного напряженного состояния
Рисунок 4.12 – Круговая диаграмма напряжений для объемного напряженного состояния
Рассмотрим еще одно напряженное состояние, которое может возникать в исследуемом теле, породном массиве, при испытании на срез. Если по граням элемента, вырезанного вокруг точки, действуют только касательные напряжения, то такое напряженное состояние называется чистым сдвигом (рисунок 4.13).
Рисунок 4.13 – Чистый сдвиг
При действии касательных напряжений элемент деформируется (рисунок 4.13, б), вертикальные грани поворачиваются на угол γ, этот угол еще называют угловой деформацией. Закон Гука при сдвиге имеет вид
где G - модуль сдвига,
Главные направления расположены под углом α = 450 и равны σ1 = τ; σ2 = 0; σ3 = - τ.
При объемном напряженном состоянии между компонентами напряженного и деформированного состояния существует определенная зависимость. В пределах малых деформаций эта зависимость является линейной и носит название обобщенного закона Гука. Наиболее простую форму обобщенный закон Гука принимает для изотропного тела, в этом случае коэффициент пропорциональности между компонентами напряженного и деформированного состояний не зависят от ориентации осей в точке.
Рисунок 4.14 – Круговая диаграмма при чистом сдвиге
Чтобы получить аналитическое выражение обобщенного закона Гука, необходимо воспользоваться принципом независимости действия сил. Линейные деформации в направлении действие напряжений σ1, σ2, σ3 определяются по формулам
Для оценки опасности напряженного состояния необходимо определить потенциальную энергию деформации при объемном напряженном состоянии. Потенциальная энергия, накопленная в элементарном объеме, определяется суммой работ сил, распределенных по поверхности этого объема. Нормальная сила σ, dy, dz (рис. 4.6, а) на перемещении ε1 dx совершает работу
Аналогичные выражения работ дают и остальные нормальные составляющие. Если потенциальную энергию отнести к единице объема с учетом выражений (4.13), то получим удельную потенциальную энергию деформации
Получим выражения для так называемой энергии изменения формы и энергии изменения объема. Эти выражения потребуются в дальнейшем при изучении вопросов, связанных с пластическими деформациями и предельными напряженными состояниями. Деление внутренней потенциальной энергии на две указанные составляющие является условным и выполняется по следующему принципу. Каждое из главных напряжений представляем в виде суммы двух величин (рисунок 4.15)
а второе является дополнением к нему до заданного напряженного состояния.
Рисунок 4.15 – Представление напряженного состояния
При указанном условии система сил первого напряженного состояния (σ0) не производит работы на перемещениях, вызванных силами второго состояния. Точно так же и силы второго напряженного состояния не производят работы на перемещениях первого. И внутренняя энергия разбивается на две части, соответствующие двум напряженным состояниям
где Uоб - потенциальная энергия изменения объема; Uф – потенциальная энергия изменения формы, или энергия формоизменения. Подставляя значения напряжений в уравнение (4.14), получаем для первого напряженного состояния
для второго напряженного состояния
Представленные выше зависимости широко используются в расчетной практике.
Теории прочности пород
Прочность породы определяется величиной критических напряжений, при которых происходит ее разрушение. Эти напряжения различны для разных пород и разных способов приложения нагрузки. Они называются пределы прочности (временное сопротивление). Различают пределы прочности пород при сжатии σвс, растяжении σвр, сдвиге τсдв, изгибе σизг и т.д. Разрушение – это разрыв связей между атомами в кристаллической решетке. Как показывают расчеты, предел прочности при растяжении должен быть равен 1 · 104 МПа. Однако в связи с тем, что реальные тела обладают множеством дефектов, значения предела прочности в сотни тысяч раз меньше теоретического значения. Дефекты могут быть различные. В кристалле – это точечные (вакансии) и линейные (дислокации) искажение кристаллической решетки. В породе – границы зерен (плоскостные) и поры (объемные искажения) и нарушения строения породы. В зависимости от масштаба разрушения породы преобладают те или иные дефекты. Существует несколько масштабов (уровней) разрушения пород. Мегаскопический уровень разрушения характерен для взрывания массивов пород, сдвижений и обвалов их. В том случае наиболее сильно на разрушаемости сказываются крупные трещины. Более мелкие трещины, поры, контакты между агрегатами зерен предопределяет разрушение макроскопическое – выемочными агрегатами (экскаваторами, комбайнами), буровыми инструментами. Микроскопический уровень разрушения характерен для измельчения полезных ископаемых в мельницах и, частично, при бурении скважин. На этой стадии происходит разрыв связей в кристаллах и зернах. При этом существенную роль играют дислокации и вакансии. Разрушение пород имеет либо хрупкий, либо пластичный характер. При хрупком разрушении происходит отрыв атомов друг от друга по всей плоскости разрушения, на что требуются большие усилия, чем при пластическом. Мелкие трещины, поры, неоднородности, плоскости ослабления предопределяют преобладающий хрупкий характер разрушения горных пород, поэтому механизм их разрушения может быть описан посредством теории хрупкого разрушения, согласно которой решающее значение для начала разрушения имеют критические трещины в объеме твердого тела. На краях трещины обычно возникают напряжения, значительно превышающие средние напряжения σ. Это явление называется концентрацией напряжений. Так, при длине трещины 2ℓ и радиусе ее закрепления на конце r (рисунок 4.16) напряжения на краю трещины равны
Рисунок 4.16 – Концентрация напряжений на краях трещины длиной 2ℓ и с радиусом закругления r (числа указывают кратность превышения напряжений σ1 над σ): а – при нагружении перпендикулярно трещине; б – при нагружении параллельно ей.
Как только напряжение σ1 достигнет определенного значения, трещина начнет развиваться, преодолевая при этом молекулярные силы сцепления (производя работу Ws, пропорциональную удельной поверхностной энергии еs данного тела)
где φℓ – площадь двух поверхностей трещины, приходящаяся на единицу поперечного размера породы. Упругая энергия, запасенная в породе в результате действия внешней нагрузки и необходимая для образования трещины
Трещина будет расти, если
Отсюда предел прочности при растяжении
При действии сжимающей нагрузки трещины смыкаются и на их поверхности появляются силы трения. В том случае предел прочности на сжатие больше предела прочности при растяжении σвс > σвр и их отношение подчиняется уравнению
где tqφ – коэффициент внутреннего трения (tqφ = 0,2…2). Например, для гранита σвс = 141 МПа, σвр = 11 МПа, На основании теории хрупкого разрушения получаем Кинетическая (термофлуктуационная) теория разрушения твердых тел, разработанная академиком С.Н. Журковым построена на том, что разрушение в некоторой зоне не является каким-то критическим состоянием тела. В соответствии с этой теорией в твердых телах непрерывно идет процесс накопления повреждений, которое приводит к полному разрушению тел. Время существования тела при действии нагрузки в не разрушенном состоянии определяется по следующей формуле
где to – константа, совпадающая по порядку с периодом колебаний атомов и не зависящая от химического состава и структуры тела (to≈10-12с); Uo – энергия активации процесса разрушения, структурно-нечувствительная величина (для гранитов Uo ≈ 2,9 ∙ 10-19 Дж; для кварцитов Uo ≈ 5,8 ∙ 10-19 Дж); V – активационный объем, зависящий от структуры тела и составляющий 103…104 атомных объемов (для гранитов V = 1,5 ∙ 10-27 м3, для кварцитов V = 1,9 ∙ 10-27 м3); kТ –- мера энергии тепловых флуктуаций; k – постоянная Больцмана k = 1,38 ∙ 10-23 Дж/к; Т – абсолютная температура тела. Предел прочности при растяжении равен
т.е. предел прочности зависит от параметров Uo и V, температуры тела и длительности действия на него нагрузки. Эксперименты, проведенные на породах, подтверждают снижение прочности с увеличением длительности действия нагрузки (рисунок 4.17).
Рисунок 4.17 – Кривые длительной прочности песчанистого сланца Донбасса (1) и известняка (2)
Прочность пород, соответствующая той или иной длительности действия нагрузки, называется их длительной прочностью σдл. С увеличением времени действия нагрузки величина длительной прочности σдл падает по кривой, асимметрически приближаясь к некоторому предельному значению, называемому пределом длительной прочности σ∞. Предел длительной прочности для многих пород равен σ∞ = (0,7…0,8) σвс. Для оценки прочности горных пород в случае сложного напряженного состояния используют критерии, позволяющие заменить сложное напряженное состояние одноосным напряженным состоянием, для которого пределы прочности могут быть определены путем теоретических исследований, либо путем эксперимента. Горные породы в подавляющем большинстве можно отнести к хрупким, поэтому при расчетах можно использовать теорию Сен-Венана (2 теория прочности) – теорию наибольших линейных деформаций. Если наибольшая линейная деформация достигла предельного значения, то напряженное состояние считается опасным.
где μ – коэффициент Пуассона. Для оценки разрушения пластичных можно применять теорию наибольших касательных напряжений (теория Кулона; третья теория прочности). Напряженное состояние считается опасным, если наибольшие касательные напряжения достигли предельного значения.
Экспериментальная проверка этой гипотезы показала, что для пластичных материалов она приводит, в общем, к удовлетворительным результатам. Переход от упругого состояния к пластическому действительно с достаточной точностью определяется разностью между наибольшим и наименьшим из главных напряжений и слабо зависит от промежуточного главного напряжения σ2. Наложение всестороннего давления на любое напряженное состояние не меняет величины наибольших касательных напряжений τmax и, следовательно, не оказывает влияние на возникновение пластических деформаций. В частности, при всестороннем гидростатическом давлении τmax обращается в нуль, следовательно, в материале не возникают пластические деформации. Наложение всестороннего давления влияет не на условие пластичности, а на условия разрушения. Граница разрушения отодвигается, и материал приобретает способность пластически деформироваться без разрушения, что объясняет поведение горных пород при определенных условиях. Рассмотрим э нергетическую теорию прочности (4 теория прочности) Представим напряженное состояние (рисунок 4.19)в виде двух напряженных состояний: всестороннее растяжение, где Первое напряженное состояние вызывает изменение объема элемента без изменения формы (куб до деформации остается кубом и после деформации), второе напряженное состояние вызывает изменение формы элемента (куб превращается в параллелепипед) без изменения объема. Напряженное состояние считается опасным, если удельная потенциальная энергия изменения формы достигла предельного значения. Эквивалентные напряжения определяются по формуле
Эта теория хорошо согласуется с экспериментом. Кроме того, перестановка местами индексов напряжений 1, 2, 3 в выражении не меняет величины эквивалентных напряжений. К вопросу прочности, согласно теории прочности Мора, можно подойти и с других позиций – с позиций упрощенной систематизации экспериментальных данных. Для хрупких тел, к которым относятся стекло, бетон, горные породы, критерий разрушения может быть сформулирован в принципе так же, как и критерий пластичности, в виде некоторого соотношения между компонентами тензора напряжений
Если Условие Мора: разрушение происходит тогда, когда на некоторой площадке величина касательного напряжения достигает критического значения, зависимо от действующего на этой площадке нормального напряжения
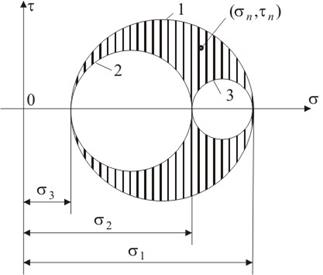
Это условие (4.34) необходимо записать в зависимости от главных напряжений. Для этого воспользуемся геометрическим представлением напряженного состояния в виде круговой диаграммы Мора. При объемном напряженном состоянии, с учетом принятых обозначений, можно построить три окружности Мора (рисунок 4.18). Точка, соответствующая определенному напряженному состоянию, с координатами σn, τn лежит в заштрихованной области, т.е. не может выйти за пределы большого круга, построенного на напряжениях σ2 и σ4.
Рисунок 4.18 – Круговая диаграмма для объемного напряженного состояния
Предположим, что мы располагаем испытательной машиной, на которой в образце можно создавать любые напряженные состояния с пропорциональным изменением всех компонент. Выберем некоторое напряженное состояние и будем одновременно увеличивать все компоненты. При некоторых значениях напряжений напряженное состояние станет предельным. Образец либо разрушится, либо в нем возникнут пластические деформации. Начертим один из наибольших кругов Мора для этого напряженного состояния (круг 1, рисунок 4.19). На образце из того же материала проводим испытание при другом напряженном состоянии, добиваемся, что напряженное состояние становятся предельным (круг 2, рисунок 4.19). В результате испытаний получаем семейство кругов Мора для различных предельных состояний. Вычеркиваем их общую огибающую кривую (рисунок 4.19). Эта огибающая кривая является единственной, независимо от главных напряжений σ2. Это основное допущение в этой теории прочности. Форма огибающей предельных кругов Мора зависит от свойств материала и является механической характеристикой материала. Проверка прочности проводится достаточно просто. Если окружность большого круга Мора не касается предельной кривой, разрушение н
|
||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 714; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.227.21.70 (0.014 с.) |

 (4.1)
(4.1)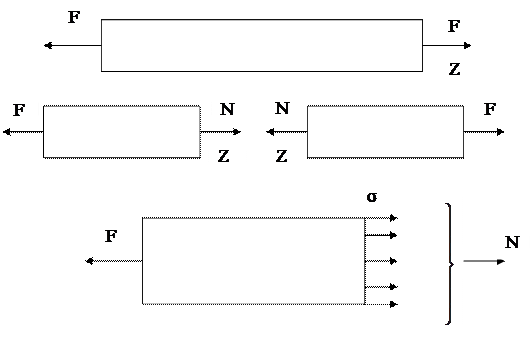

 , Па, (4.1)
, Па, (4.1) (4.2)
(4.2) , (4.3)
, (4.3) (4.4)
(4.4)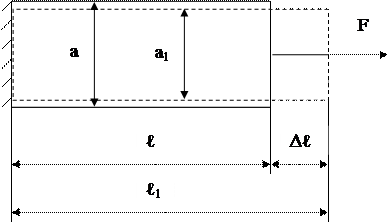

 (4.5)
(4.5) , (4.6)
, (4.6)


 ,
,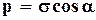 .
. , (4.7)
, (4.7)
 .
. , (4.8)
, (4.8)
 ,
, ;
;  ;
;  (4.9)
(4.9)

 ,
,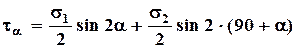 ,
,
 (4.10)
(4.10)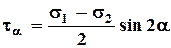 .
. , (4.10, а)
, (4.10, а) от начала координат по оси σ. Радиус окружности равен
от начала координат по оси σ. Радиус окружности равен  .
.
 Эта окружность носит название круг Мора или круговой диаграммой напряженного состояния. Каждая площадка имеет координаты σ, τ. Точки, соответствующие двум взаимно перпендикулярным площадкам, на круге напряжений расположены диаметрально противоположно. Следовательно, зная напряжения на двух взаимно перпендикулярных площадках можно построить окружность. Координаты вертикальной площадки (σ1; 0), горизонтальной (σ2; 0).
Эта окружность носит название круг Мора или круговой диаграммой напряженного состояния. Каждая площадка имеет координаты σ, τ. Точки, соответствующие двум взаимно перпендикулярным площадкам, на круге напряжений расположены диаметрально противоположно. Следовательно, зная напряжения на двух взаимно перпендикулярных площадках можно построить окружность. Координаты вертикальной площадки (σ1; 0), горизонтальной (σ2; 0).

 Если заданы площадки общего положения, по которым действуют нормальные и касательные напряжения, определяемые при том или ином методе расчета, то координаты точек, соответствующих вертикальным и горизонтальным площадкам соответственно (σх, τух), горизонтальной (σу, τух) (рисунок4.9, а). Для построения круга напряжений примем, что в данном случае σх > σу. Центр круга имеет координату
Если заданы площадки общего положения, по которым действуют нормальные и касательные напряжения, определяемые при том или ином методе расчета, то координаты точек, соответствующих вертикальным и горизонтальным площадкам соответственно (σх, τух), горизонтальной (σу, τух) (рисунок4.9, а). Для построения круга напряжений примем, что в данном случае σх > σу. Центр круга имеет координату  , радиус круга равен
, радиус круга равен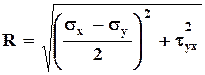 (4.11)
(4.11)
 ,
, .
. , (4.12)
, (4.12) . (4.13)
. (4.13) . (4.14)
. (4.14)
 . (4.15)
. (4.15)


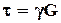 , (4.16)
, (4.16) . (4.17)
. (4.17)
 Графическое представление этого напряженного состояния (координаты точек соответствующих площадок (0; - τ), (0; τ)) дано на рисунке 4.14. Полюс круга находится в точке В, направление главных напряжений определяется прямыми ВС и ВД.
Графическое представление этого напряженного состояния (координаты точек соответствующих площадок (0; - τ), (0; τ)) дано на рисунке 4.14. Полюс круга находится в точке В, направление главных напряжений определяется прямыми ВС и ВД.
 ,
, , (4.18)
, (4.18) .
. .
. (4.19)
(4.19) ;
;  ;
;  , (4.20)
, (4.20)
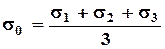 , (4.21)
, (4.21) ,
, , (4.22)
, (4.22) (4.23)
(4.23)

 ,
, , (4.24)
, (4.24) . (4.25)
. (4.25)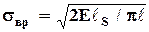 . (4.26)
. (4.26) , (4.27)
, (4.27)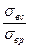 = 13, песчаника кварцевого σвс = 164 МПа, σвр = 6,6 МПа,
= 13, песчаника кварцевого σвс = 164 МПа, σвр = 6,6 МПа,  , (4.28)
, (4.28) , (4.29)
, (4.29)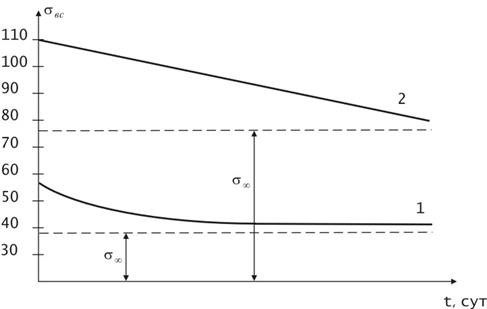
 , (4.30)
, (4.30) (4.31)
(4.31) и во втором напряженном состоянии, где по граням элемента действуют напряжения σ1 – σо, σ2 – σо, σ3 – σо.
и во втором напряженном состоянии, где по граням элемента действуют напряжения σ1 – σо, σ2 – σо, σ3 – σо. (4.32)
(4.32) . (4.33)
. (4.33) , то материал не разрушается. При выполнении условия (4.33) хотя бы в одной точке – происходит локальное разрушение. Под локальным разрушением понимают либо разрыв, разрушение и срез некоторых структурных элементов, либо появление зародышевой трещины или слияние с трещинами, возникшими в соседних точках, где выполняется условие (4.33). Область локального разрушения служит источником концентрации напряжений, поэтому вероятно использование новых очагов разрушения по соседству с уже возникшими.
, то материал не разрушается. При выполнении условия (4.33) хотя бы в одной точке – происходит локальное разрушение. Под локальным разрушением понимают либо разрыв, разрушение и срез некоторых структурных элементов, либо появление зародышевой трещины или слияние с трещинами, возникшими в соседних точках, где выполняется условие (4.33). Область локального разрушения служит источником концентрации напряжений, поэтому вероятно использование новых очагов разрушения по соседству с уже возникшими. . (4.34)
. (4.34)