
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Интегральный признак Коши-МаклоренаСодержание книги Поиск на нашем сайте
(Маклорен Колин (1698 – 1746) – шотландский математик, ученик И.Ньютона.) Теорема 14. Если функция
и несобственный интеграл:
– сходятся или расходятся одновременно. Если ряд (3.3) и интеграл (3.4) сходятся, то справедливы следующие оценки:
где Пример 44. Рассмотрим обобщенный гармонический ряд При
Рассмотрим три случая: 1) если 2) если 3) если
Если Итак, ряд Пример 45. Исследовать на сходимость ряд Введем функцию
Из последнего равенства видно, что данный интеграл сходится, если Следовательно, исследуемый ряд сходится при Пример 46. Исследовать на сходимость ряд В этом случае непосредственное применение интегрального признака нецелесообразно, т.к. вычисление несобственного интеграла может оказаться затруднительным. Сравним общий член данного ряда с общим членом ряда
Так как ряд Пример47. Исследовать сходимость ряда Так как Пусть
Вывод: ряд Пример 48. Выясним, сколько членов ряда Введем функцию
Замечание. При решении данной задачи можно было воспользоваться и оценкой (3.5). Метод выделения главной части При исследовании на сходимость ряда
В случае (3.7) ряд Пример 49. Исследовать сходимость ряда Здесь Пример 50. Исследовать сходимость ряда Пример 51. Исследовать сходимость ряда Окончательно получаем: исходный ряд сходится при Пример 52. Исследовать сходимость ряда Используя разложения:
Знакопеременные ряды Знакопеременный ряд – это ряд, членами которого являются вещественные числа произвольного знака. Определение. Ряд
называется абсолютно сходящимся, если сходится ряд, составленный из модулей его членов:
Определение. Сходящийся ряд (2.1) называют условно сходящимся, если ряд (2.2) расходится.
|
|||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 551; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.4.50 (0.01 с.) |

 неотрицательна и не возрастает на промежутке
неотрицательна и не возрастает на промежутке 
 то ряд:
то ряд: (3.3)
(3.3) (3.4)
(3.4) (3.5)
(3.5) (3.6)
(3.6) Заметим, что оценка сверху в неравенстве (3.6) является следствием оценки сверху в неравенстве (3.5).
Заметим, что оценка сверху в неравенстве (3.6) является следствием оценки сверху в неравенстве (3.5).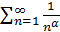 ,
, 
 0 функция
0 функция  положительна, убывает на промежутке
положительна, убывает на промежутке 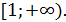 При
При  имеем:
имеем:
 то при
то при  следовательно,
следовательно,  т.е. интеграл расходится, а значит расходится и ряд (это мы установили выше другим способом);
т.е. интеграл расходится, а значит расходится и ряд (это мы установили выше другим способом); , то исходный ряд превращается в гармонический ряд, расходимость которого была доказана в п. 1.1, (впрочем, интеграл
, то исходный ряд превращается в гармонический ряд, расходимость которого была доказана в п. 1.1, (впрочем, интеграл  также расходится);
также расходится); , то ряд
, то ряд  следовательно,
следовательно, 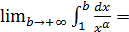
 т.е. несобственный интеграл сходится, а значит и ряд сходится.
т.е. несобственный интеграл сходится, а значит и ряд сходится. , то ряд
, то ряд 
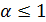 .
. .
. На промежутке
На промежутке  эта функция принимает положительные значения, а ее производная равна
эта функция принимает положительные значения, а ее производная равна . Если
. Если  т.е.
т.е.  , то
, то  . Следовательно,
. Следовательно,  положительная функция и убывает на промежутке
положительная функция и убывает на промежутке  , где
, где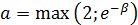 . Рассмотрим несобственный интеграл:
. Рассмотрим несобственный интеграл: .
.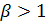 , и расходится, если
, и расходится, если  .
. .
.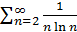 . Найдем:
. Найдем:


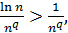 если
если  то в силу теоремы сравнения данный ряд расходится при
то в силу теоремы сравнения данный ряд расходится при 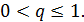
 . Так как по правилу Лопиталя
. Так как по правилу Лопиталя  при
при  , то, в частности, для
, то, в частности, для  найдется номер
найдется номер  , такой, что
, такой, что 
 Число
Число  , где
, где  Тогда
Тогда  , и так как обобщенный гармонический ряд
, и так как обобщенный гармонический ряд  при
при 
 сходится для всех значений
сходится для всех значений  и
и 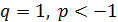 (см. пример 45).
(см. пример 45). надо сложить, чтобы найти сумму этого ряда с точностью до 0,001.
надо сложить, чтобы найти сумму этого ряда с точностью до 0,001. ,
, 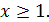 по формуле (3.6)
по формуле (3.6) или
или 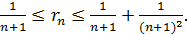 Так как требуемая погрешность не должна превосходить 0,001, то потребуем, чтобы
Так как требуемая погрешность не должна превосходить 0,001, то потребуем, чтобы  Тогда при
Тогда при  значит для вычисления суммы ряда с требуемой точностью следует сложить по меньшей мере 1000 членов ряда! Как видим, сходимость ряда весьма «медленная».
значит для вычисления суммы ряда с требуемой точностью следует сложить по меньшей мере 1000 членов ряда! Как видим, сходимость ряда весьма «медленная». с неотрицательными членами полезны асимптотические формулы вида:
с неотрицательными членами полезны асимптотические формулы вида: (3.7)
(3.7) (3.8)
(3.8) или
или  и в других случаях расходится.
и в других случаях расходится.
 при
при  так как последовательность
так как последовательность  является бесконечно малой при
является бесконечно малой при  ряд с общим членом
ряд с общим членом  согласно (3.8) расходится, поэтому ряд также расходится.
согласно (3.8) расходится, поэтому ряд также расходится. Общий член данного ряда
Общий член данного ряда  Здесь
Здесь  и согласно (3.8) исходный ряд сходится.
и согласно (3.8) исходный ряд сходится. Заметим, что при
Заметим, что при 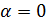 предел
предел  не существует, так как не существует предел
не существует, так как не существует предел  ; если
; если  то
то 
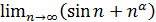 не существует, и общий член ряда не стремится к нулю. Следовательно, при
не существует, и общий член ряда не стремится к нулю. Следовательно, при  Так как
Так как 
 , то
, то  Согласно (3.7) данный ряд сходится при
Согласно (3.7) данный ряд сходится при 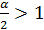 и расходится при
и расходится при 
 и расходится при
и расходится при 


 находим
находим 
 Следовательно,
Следовательно,  т.е.
т.е.  и поэтому ряд сходится.
и поэтому ряд сходится. (2.1)
(2.1) (2.2)
(2.2)


