
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Сходящиеся и расходящиеся рядыСодержание книги Поиск на нашем сайте
Пусть задана последовательность (an) действительных чисел a1, a2, a3, …,an, …. (1.1) Сопоставим этой последовательности чисел последовательность (Sn) конечных сумм вида: S1=a1, S2=a1+a2, S3=a1+a2+a3, …, Sn=a1+a2+…+an,… Однако на практике часто приходят к задачам суммирования бесконечной последовательности чисел (1.1). В этом случае вместо слов последовательность (an) и последовательность (Sn) употребляют слово ряд. Для обозначения ряда используют символы: a1+a2+…+an+… или
Число Так как каждому ряду Таким образом, фразы «последовательность (an)», «последовательность (Sn)», «совокупность последовательностей (an) и (Sn)», «ряд При определении ряда естественно возникают вопросы: 1. Что такое «сумма» бесконечной последовательности чисел? 2. Если сумма существует, то каковы ее свойства? Прежде чем ответить на эти вопросы, рассмотрим следующие примеры. Пример 1. Отрезок [1,0] разобьем пополам (на два равных отрезка).
Правую половину отрезка, то есть отрезок [1/2, 1], снова разделим пополам, затем разобьем пополам отрезок [3/4, 1] и т. д. Продолжая этот процесс до бесконечности, получим разбиение отрезка [0, 1] на бесконечное множество отрезков: [0, 1/2], [1/2, 3/4], [3/4, 7/8], [7/8, 5/16],… Естественно считать, что «сумма» длин всех отрезков, на которые разбит отрезок [0, 1], равна длине отрезка, т.е. единице. Иными словами,
Это рассуждение было известно еще грекам, и философ Зенон (ок. 490 г. до н.э.), известный своими «парадоксами», оспаривал его законность. Один из парадоксов утверждал, что бегущий человек никогда не сможет достичь своей цели, поскольку он должен пробежать сначала половину требуемой дистанции, затем половину оставшейся части дистанции и т. д.; таким образом, он должен пробежать бесконечное множество расстояний, а это будет продолжаться вечно. Если бы мы попытались вычислить сумму (1.3), последовательно выполняя все указанные в ней сложения, то это, конечно, никогда бы не окончилось. И все-таки равенство (1.3) в некотором смысле верно. В чем же заключается точный его смысл? Определим понятие суммы ряда. Прежде обратимся к примеру 1. Последовательности
Ясно, что Определение. Если последовательность (Sn) частичных сумм ряда сходится, то ее предел
Если Если Пример 2. Рассмотрим ряд Для этого ряда Пример 3. Рассмотрим ряд Пример 4. Рассмотрим последовательность
Ей соответствует ряд Не существует каких-либо общих методов нахождения сумм сходящихся рядов. Эту задачу удается решить только в отдельных частных случаях. Пример 5. Исследуем сходимость Так как Замечание. Для представления общего члена ряда в виде суммы простейших дробей полезно использовать метод неопределенных коэффициентов. Пример 6. Исследуем на сходимость ряд Представим общий член ряда
Умножая обе части этого равенства на знаменатель левой части, приходим к тождеству: 1≡ A (n +1)(n +2)+ Bn (n +2)+ Cn (n +1). Последовательно полагая n =0, -1, -2, находим: Таким образом, Отсюда:
следовательно, данный ряд сходится и его сумма Пример 7. Исследуем на сходимость ряд Преобразуем формулу n -го члена ряда, представив его в виде суммы простейших дробей:
Следовательно, ряд сходится и его сумма Пример 8. Выясним, сходится или расходится ряд Частичные суммы ряда равны:
Имеем Пример 9. Пусть m –фиксированное натуральное число. Исследуем на сходимость ряд Преобразуем общий член ряда по формуле
Выпишем последовательность частичных сумм данного ряда:
Так как Пример 10. Пусть члены ряда
Тогда исходный ряд сходится и его сумма равна
Действительно,
Так как Применим данное свойство для ряда с общим членом:
Представим его в виде:
Обозначим
Пример 11. Найдем сумму ряда Так как Отсюда: Рассмотрим так называемые эталонные ряды, которые часто используются при исследовании сходимости многих рядов. Пример 12. Исследуем сходимость гармонического [1]ряда:
Его частичная сумма
Таким образом, Приведем еще одно доказательство того, что гармонический ряд
Но Заметим, что гармонический ряд расходится очень «медленно». Л.Эйлер, например, вычислил, что (Леонард Эйлер (1707– 1783) – математик, физик, механик; родился в Швейцарии, большую часть жизни прожил в России и в Германии, активно участвовал во многих направлениях деятельности Петербургской и Берлинской академий.) Пример 13. Ряд Здесь Пример 14. Исследуем на сходимость ряд Преобразуем частичную сумму
Отсюда сумма равна В частности, если 1. 2. Число e как сумма ряда Нам известно, что По формуле бинома Ньютона:
Полагая
С другой стороны, при любом фиксированном k и любом
При
Оценим разность
Таким образом, чтобы абсолютная погрешность приближения числа e числом В заключение покажем, что число e иррационально. Предположим, что С другой стороны, В 1873 году Ш. Эрмит (Шарль Эрмит (1822-1901) – французский математик, член Парижской Академии наук) установил, что число e трансцендентно, т.е. не является корнем никакого алгебраического многочлена с целыми коэффициентами.
|
||||||||||
|
Последнее изменение этой страницы: 2016-09-18; просмотров: 1213; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.22.75.247 (0.006 с.) |

 (1.2)
(1.2) называют n-й частичной суммой ряда
называют n-й частичной суммой ряда  , а число an – n-м (общим) членом этого ряда.
, а число an – n-м (общим) членом этого ряда.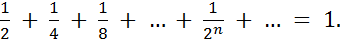 (1.3)
(1.3) сопоставим последовательность частичных сумм (Sn), где
сопоставим последовательность частичных сумм (Sn), где
 является длиной отрезка.
является длиной отрезка. называют суммой ряда, а сам ряд (1. 2) называют сходящимся или суммируемым. В этом случае пишут:
называют суммой ряда, а сам ряд (1. 2) называют сходящимся или суммируемым. В этом случае пишут:
 , или предел последовательности
, или предел последовательности  не существует, то ряд
не существует, то ряд 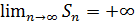 , то говорят, что ряд
, то говорят, что ряд 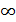 , и пишут
, и пишут  Аналогично в случае
Аналогично в случае  считаем, что
считаем, что 
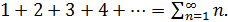
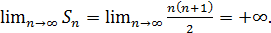 Данный ряд расходится к +
Данный ряд расходится к +  Поскольку для этого ряда
Поскольку для этого ряда 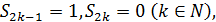 то последовательность
то последовательность  . Следовательно, ряд
. Следовательно, ряд  расходится. Заметим, что этот ряд не расходится ни к
расходится. Заметим, что этот ряд не расходится ни к  ни к
ни к 

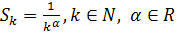 .
. Так как последовательность
Так как последовательность  и расходится при
и расходится при  то и ряд
то и ряд  сходится при
сходится при 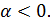
 и найдем его сумму.
и найдем его сумму.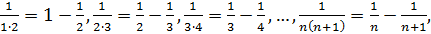 то последовательность частичных сумм
то последовательность частичных сумм  имеет
имеет  . Итак, заданный ряд сходится и его сумма
. Итак, заданный ряд сходится и его сумма 
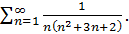
 в виде суммы простейших дробей:
в виде суммы простейших дробей:
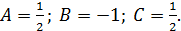


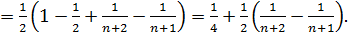 Ясно, что
Ясно, что 


 Выпишем последовательность частичных сумм данного ряда и найдем ее предел:
Выпишем последовательность частичных сумм данного ряда и найдем ее предел: 






 т.к. аргумент логарифма, а значит и сам логарифм при
т.к. аргумент логарифма, а значит и сам логарифм при  стремятся к бесконечности. Следовательно, исследуемый ряд расходится.
стремятся к бесконечности. Следовательно, исследуемый ряд расходится. называемый рядом обратных факториалов.
называемый рядом обратных факториалов.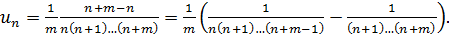



 то
то 
 и пусть существует конечный предел:
и пусть существует конечный предел: 
 т.е.
т.е. (1. 4)
(1. 4) т.е.
т.е. 
 то отсюда получаем
то отсюда получаем  и поэтому справедлива формула (1. 4).
и поэтому справедлива формула (1. 4).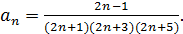

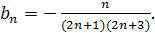 Тогда
Тогда  причем
причем 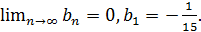 По формуле (1. 4) находим:
По формуле (1. 4) находим: 


 то
то 

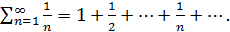
 Пусть
Пусть 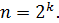 Тогда
Тогда

 Последовательность
Последовательность  не ограничена сверху, а потому не может быть сходящейся, так как сходящаяся последовательность ограничена. Следовательно, ряд
не ограничена сверху, а потому не может быть сходящейся, так как сходящаяся последовательность ограничена. Следовательно, ряд  расходится.
расходится. расходится. Действительно, если бы он сходился, то, обозначив его сумму через S, мы бы имели:
расходится. Действительно, если бы он сходился, то, обозначив его сумму через S, мы бы имели: (1.5)
(1.5) т.е.
т.е.  что противоречит (1.5).
что противоречит (1.5).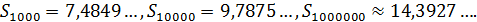
 называется обобщенным гармоническим. При
называется обобщенным гармоническим. При  - это гармонический ряд, и его расходимость доказана. Покажем, что этот ряд расходится и при
- это гармонический ряд, и его расходимость доказана. Покажем, что этот ряд расходится и при 
 и
и  при любом
при любом  . Следовательно,
. Следовательно, 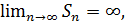 и поэтому при
и поэтому при 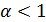 данный ряд расходится. Итак, обобщенный гармонический ряд расходится при
данный ряд расходится. Итак, обобщенный гармонический ряд расходится при  Ниже будет доказано, что при
Ниже будет доказано, что при  этот ряд сходится.
этот ряд сходится. где q -действительное число:
где q -действительное число: 
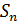 этого ряда следующим образом:
этого ряда следующим образом:


 Следовательно, ряд
Следовательно, ряд  сходится и его
сходится и его
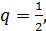 то
то 
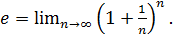 В этом пункте мы изучим ряд, с помощью которого можно указать достаточно хороший способ вычисления числа e.
В этом пункте мы изучим ряд, с помощью которого можно указать достаточно хороший способ вычисления числа e.


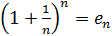 и
и  имеем
имеем
 из того же разложения имеем:
из того же разложения имеем:
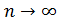 левая часть последнего неравенства стремится к
левая часть последнего неравенства стремится к  , а правая – к числу e, поэтому
, а правая – к числу e, поэтому 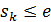 для любого
для любого  Но тогда из двойного неравенства
Но тогда из двойного неравенства  по известной теореме о пределе промежуточной последовательности получаем, что
по известной теореме о пределе промежуточной последовательности получаем, что  По определению суммы ряда теперь можно записать:
По определению суммы ряда теперь можно записать:

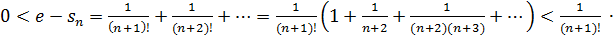

 не превосходила, например,
не превосходила, например, 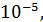 достаточно, чтобы имело место неравенство
достаточно, чтобы имело место неравенство  . Этому условию удовлетворяет уже
. Этому условию удовлетворяет уже 
 где
где  Тогда при любом
Тогда при любом  число
число 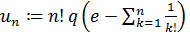 целое и положительное. Следовательно,
целое и положительное. Следовательно,  при любом
при любом 
 Противоречие!
Противоречие!


