
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Необходимый признак сходимости числового рядаСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нахождение Теорема. Если ряд (1) сходится, то его общий член
Следствие (достаточное условие расходимости ряда). Если Пример: исследовать сходимость ряда
Достаточные признаки сходимости знакопостоянных рядов Рассмотрим некоторые из достаточных признаков сходимости знакоположительных рядов, т.е. рядов с Признаки сравнения рядов. Сходимость или расходимость ряда часто устанавливается путем сравнения его с другим (эталонным) рядом, о котором известно сходится он или нет. В основе такого сравнения лежат следующие теоремы. Теорема 1. пусть даны два знакоположительных ряда Доказательство: Из неравенства Теорема.2. (предельный признак сравнения). Пусть даны два знакоположительных ряда
Признак Даламбера В отличие от признаков сравнения, где все зависит от догадки и записи известных сходящихся и расходящихся рядов признак Даламбера позволяет решить вопрос о сходимости ряда, проделав лишь некоторые операции над самим рядом. Теорема. Пусть дан ряд с положительными членами и существует конечный или бесконечный предел Доказательство: Так как Пусть
………..
Т.е. члены ряда Пусть 1) Если 2) Признак Даламбера целесообразно применять, когда общий член ряда содержит выражения вида Пример. Исследовать на сходимость ряд
Радикальный признак Коши Иногда удобно пользоваться радикальным признаком Коши для исследования сходимости знакоположительного ряда. Этот признак во многом схож с признаком Даламбера. Теорема. Пусть дан ряд При Пример. Исследовать на сходимость ряд
|
||||
|
Последнее изменение этой страницы: 2016-12-14; просмотров: 523; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.174.45 (0.011 с.) |

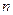 -й частичной суммы
-й частичной суммы 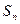 и ее предела для произвольного ряда во многих случаях является задачей весьма непростой. Поэтому для выяснения сходимости ряда устанавливают специальные признаки сходимости. Первым из них является необходимый признак сходимости.
и ее предела для произвольного ряда во многих случаях является задачей весьма непростой. Поэтому для выяснения сходимости ряда устанавливают специальные признаки сходимости. Первым из них является необходимый признак сходимости.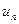 стремится к нулю, т.е.
стремится к нулю, т.е.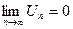 Пусть ряд расходится и
Пусть ряд расходится и  , тогда и
, тогда и 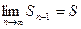 . Учитывая, что
. Учитывая, что 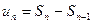 при
при 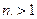 , получаем
, получаем 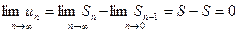 . ч.т.д.
. ч.т.д. или этот предел не существует, то ряд расходится.
или этот предел не существует, то ряд расходится. ;
; 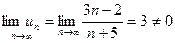 , т.е. ряд расходится. Теорема даст необходимое условие сходимости ряда, не достаточное (из условия
, т.е. ряд расходится. Теорема даст необходимое условие сходимости ряда, не достаточное (из условия  не следует, что ряд сходится). Это означает, что существуют расходящиеся ряды для которых
не следует, что ряд сходится). Это означает, что существуют расходящиеся ряды для которых 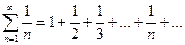 Очевидно, что
Очевидно, что  .
. и
и 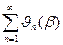 . Если для всех
. Если для всех  , то из сходимости ряда
, то из сходимости ряда 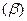 следует сходимость ряда
следует сходимость ряда  , а из расходимости ряда
, а из расходимости ряда 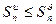 (1). Пусть ряд
(1). Пусть ряд  сходится и его сумма равна
сходится и его сумма равна 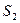 , тогда
, тогда 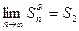 . Члены этого ряда положительны, поэтому
. Члены этого ряда положительны, поэтому 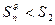 и, следовательно, с учетом неравенства (1)
и, следовательно, с учетом неравенства (1)  .таким образом последовательность
.таким образом последовательность  монотонно возрастает
монотонно возрастает 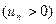 и ограничена сверху числом
и ограничена сверху числом  имеет предел
имеет предел 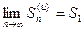 , т.е. этот ряд сходится. Если ряд
, т.е. этот ряд сходится. Если ряд 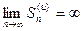 . Тогда с учетом соотношения (1) получим, что
. Тогда с учетом соотношения (1) получим, что  . Если существует конечный, отличный от 0 предел
. Если существует конечный, отличный от 0 предел 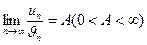 , то ряды
, то ряды  , тогда ряд сходится при
, тогда ряд сходится при 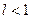 и расходится при
и расходится при  .
.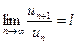 , то по определению предела для любого
, то по определению предела для любого 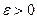 найдется натуральное число
найдется натуральное число  такое, что при
такое, что при 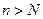 выполняется неравенство
выполняется неравенство  или
или  (2).
(2). так, что число
так, что число 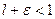 . Обозначим
. Обозначим 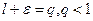 . Тогда из правой части неравенства (2) получаем
. Тогда из правой части неравенства (2) получаем 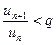 или
или 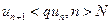 . В силу свойства 3 числовых рядов можно считать, что
. В силу свойства 3 числовых рядов можно считать, что 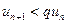 для всех
для всех 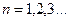 . Давая номеру
. Давая номеру 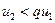
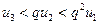
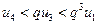
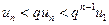
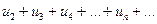 меньше соответствующих членов ряда
меньше соответствующих членов ряда 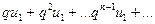 , который сходится как геометрическая прогрессия со знаменателем
, который сходится как геометрическая прогрессия со знаменателем 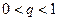 . Но тогда на основании признака сходимости сходится и ряд
. Но тогда на основании признака сходимости сходится и ряд  . Следовательно, сходится и исходный ряд
. Следовательно, сходится и исходный ряд  .
. . Отсюда следует, что, начиная с некоторого номера
. Отсюда следует, что, начиная с некоторого номера 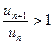 или
или 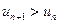 , т.е. члены ряда с увеличением номера
, т.е. члены ряда с увеличением номера 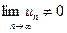 . На основании следствия из необходимого признака этот ряд расходится.
. На основании следствия из необходимого признака этот ряд расходится. , то ряд
, то ряд 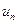 может быть как сходящимся, так и расходящимся.
может быть как сходящимся, так и расходящимся.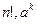 .
. . Находим
. Находим 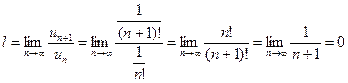 . Так как
. Так как 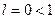 , то данный ряд по признаку Даламбера сходится.
, то данный ряд по признаку Даламбера сходится.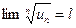 . Тогда ряд сходится при
. Тогда ряд сходится при 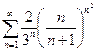 . Так как
. Так как 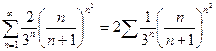 , то применим признак Коши к ряду
, то применим признак Коши к ряду 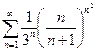 . Вычисляем
. Вычисляем 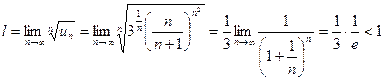 , т.е. этот ряд сходится, значит, сходится и исходный ряд согласно свойству 1 числовых рядов.
, т.е. этот ряд сходится, значит, сходится и исходный ряд согласно свойству 1 числовых рядов.


