Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема 20 (признак Даламбер)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Если существует предел Доказательство: А) пусть Рассмотрим (p,q) с центром в точке
Тогда сходится 2) пусть Значит члены ряда не убывают, следовательно ряд расходится Признак Даламбер удобно применять, когда общий ряд содержит Пример
Теорема 21. (признак Коши) Если существует конечный предел
То знакоположительный ряд Доказательство: А) пусть Из определения предела следует, что начиная с некоторого N:
Сумма бесконечно убывающей геометрической прогрессии, сходится Тогда по признаку сравнения сходится 2) пусть Это означает, начиная с некоторого n, Замечание. Признак Даламбера и признак Коши не дают ответа, в случае когда
Пример. Исследовать сходимость
Определение числа e 1) рассмотрим ряд
Покажем, что он сходится
По признаку сравнения
Оценим величину
Оценим погрешность, в которой частичная сумма
Рассмотрим разность
Погрешность от замены суммы частичной суммой не превосходит 1 Вычислить число
N=3 n=4 n=5 n=6 n=7 n=8 чтобы вычесть 2. Покажем, что
Мы получили, что
Ясно, что при
То по теореме сравнения предел тоже будет равен е Знакопеременные ряды Определение 16. Ряд Например, Теорема 22. (достаточный признак сходимости) Если сходится ряд Доказательство:
Проверим Критерий Коши для исходного ряда
Следовательно, выполняется критерий Коши и исходный ряд тоже сходится Пример.
Проверим критерий Коши, рассмотрим ряд
Следовательно сходится исходный ряд Определение 17. Знакопеременный ряд называется абсолютно сходящимся, если сходится ряд из абсолютных величин Из теоремы ясно, что если ряд абсолютно сходится, то он и просто сходится
Определение 18. Знакопеременный ряд называется условно сходящимся, если он сходится, а ряд из абсолютных величин его сходится Например, Среди всех знакопеременных рядов особое значение имеют знакочередующиеся ряды
Теорема 23. (признак Лейбница) Пусть член знакочередующегося ряда монотонно убывает
Тогда знакочередующийся ряд сходится Доказательство: Обозначим через Последовательность
А последовательность
Эти последовательности монотонные, последовательность
Четные, нечетные частичные суммы имеют один предел, следовательно
Следствие. Абсолютная погрешность при замене суммы знакочередующегося ряда частичной суммой не превосходит первого отброшенного члена
Доказательство: Так как нечетная сумма
С ледствие очень важное и играет большую роль при приближенных вычислениях с помощью рядов Пример.
Надо взять столько членов, чтобы 1-й отброшенный член не превосходил
Вернемся к произвольным знакопеременным рядам
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 1018; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.117.94.180 (0.011 с.) |

 то знакоположительный ряд
то знакоположительный ряд  сходится при
сходится при  , расходится при
, расходится при 
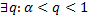
 ,тогда по определению начиная с некоторого n предел существует, так как все члены последовательности
,тогда по определению начиная с некоторого n предел существует, так как все члены последовательности  - лежат в интервале (p,q)
- лежат в интервале (p,q) можно записать
можно записать 

 - сходится как геометрическая прогрессия при
- сходится как геометрическая прогрессия при 
 , следовательно, сходится
, следовательно, сходится 
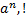 , а когда обобщенный член содержит степенные и рациональные, удобно применять признаки сравнения
, а когда обобщенный член содержит степенные и рациональные, удобно применять признаки сравнения

 по теореме ряд расходится
по теореме ряд расходится
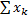 сходится при
сходится при 


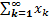 , он отличается на такое число
, он отличается на такое число  , следовательно, при
, следовательно, при 
 , не выполняется необходимый признак сходимости, следовательно ряд расходится
, не выполняется необходимый признак сходимости, следовательно ряд расходится , в этом случае применяют другие признаки
, в этом случае применяют другие признаки применим признак Коши
применим признак Коши следовательно ряд сходится
следовательно ряд сходится

 этот ряд как геометрическая прогрессия сходится, q=
этот ряд как геометрическая прогрессия сходится, q= 

 – сходится и его сумму обозначим
– сходится и его сумму обозначим




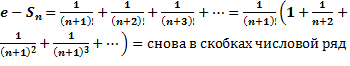

 , то есть проссумировать ряд с точностью до
, то есть проссумировать ряд с точностью до 







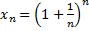

 (формула Бинома-Ньютона)
(формула Бинома-Ньютона)


 сходится и он равен
сходится и он равен 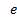 , тогда
, тогда последовательность
последовательность  - возрастает и ограничена сверху, а следовательно она сходится. Найдем её
- возрастает и ограничена сверху, а следовательно она сходится. Найдем её




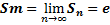
 - называется знакопеременным, если его члены могут иметь как положительные, так и отрицательные знаки
- называется знакопеременным, если его члены могут иметь как положительные, так и отрицательные знаки
 с членами из модулей то и сходится
с членами из модулей то и сходится 


 - а этот ряд сходится как обобщенно – гармонический, с показателем
- а этот ряд сходится как обобщенно – гармонический, с показателем 
 – сходится абсолютно, так как
– сходится абсолютно, так как 

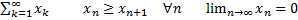
 и
и  m=1,2,3…
m=1,2,3…



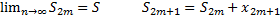

 следовательно, ряд сходится
следовательно, ряд сходится


 не возрастает и стремится к S, а
не возрастает и стремится к S, а  отсюда
отсюда