
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Геометрическая интерпретацияСодержание книги
Поиск на нашем сайте
Возьмем Х0 на числовой прямой. Зададим Е и построим Е-окрестность. Из определения следует, что по заданному Е найдется такой N, начиная с которого все члены последовательности будут расположены в этой Е- окрестности. А члены Х1, Х2, ХN – будут лежать за пределами окрестности Построим отрицание существования предела, то есть
Правило построения отрицания логического выражения:
Пример2.
В качестве
Эта функция представляет целую часть, х есть наиболее целое число, удовлетворяющее неравенство Пример 3.
От противного, пусть предел существует
Тогда, если n- четное, то
если n- нечетное
нет такого Пример 4.
Все четные члены стремятся к 0 слева, а стремятся к + В любой окрестности точки
Теорема 1. (единственность предела) Если предел последовательности существует, то он единственный Доказательство: От противного, предположим, последовательность
Возьмем
Определение 3. Числовая последовательность называется ограниченной, если существует
В противном случае, последовательность называется неограниченной. Теорема 2. Всякая сходящаяся последовательность ограничена Доказательство: Пусть
Обозначим через Тогда очевидно Это означает, что последовательность ограничена Обратное утверждение неверно
Пример 5. *
А) Зададим По определению для
В этом случае сходится Б) q=-1 ⇾ Расходится пр. 1 q = 1 В) Могут принимать любые большие значения, следовательно, последовательность неограниченна и она расходится
Определение 4 Последовательность Хn – называется неубывающей (невозрастающей) если
Называются монотонными Определение 5 Последовательность Хn – называется возрастающей (убывающей) если выполняются условия
Теорема 3. Всякая монотонная ограниченная последовательность сходится Доказательство Пусть Хn – не убывает, по условию Хn – ограничено, то есть её множество значений Х ограничено Тогда существует точная верхняя грань множества Х П усть 1) В силу монотонности это неравенство
Добавим в некоторое +
Лекция 7 § 2.2 Свойства сходящихся последовательностей Пусть Хn, Уn – числовые последовательности Определение 6. Суммой, разностью произведения и частных двух последовательностей Хn, Уn называется:
Теорема 4. Пусть последовательности Тогда сходится и последовательность Причем справедливы формулы а) б) в) г) Доказательство: а) покажем, что последовательность
так как предел
б) так как пределы
По следовательность в) по условию последовательности
Это значит, что г) доказать сведя к произведению
Теорема 5. Пусть задано три последовательности а) если
б) если
Доказательство: а) Пусть от противного Пусть
Это значит б) Пусть
Из условия б) следует
Это означает, что последовательность Пример 1. Покажем, что
Возьмем номер N такой, что
По теореме б) Пример 2.
Биномиальные коэффициенты
Ограничены первыми двумя слагаемыми, тогда, отсюда
Следовательно предел Лекция 8 Определение 7. Последовательность
Если Теорема 6. Произведение ограниченной последовательности на бесконечно малую, есть бесконечно малая последовательность Доказательство: Пусть Так как А так как Тогда это означает, что Определение 8. Последовательность Хn – называется бесконечно большой, если
Если
Теорема 7. А) если предел Б) если последовательность Доказательство: А) Пусть Следовательно последовательность
§ 2.3 Теорема Больцано-Венерштрасса. Фундаментальные последовательности Определение 9. Пусть Хn – числовая последовательность и Последовательность Если подпоследовательности Хkn сходятся, то её предел называется частичным пределом последовательности Хn { Хn }={1,⅟2, 2, ⅓, 3,⅟4, 4, ⅕ … n, ⅟n+1 …} не является на бесконечно малой ни бесконечно большой, она не ограничена, однако у неё есть частичный предел { Х2n }={⅟2, ⅓, ⅟4 …} Кn=n+1 эта последовательность сходится и число 0 является её пределом Теорема 8. Если последовательность Хn – сходится, то любая её подпоследовательность Хkn тоже сходится и имеет тот же предел Доказательство. Пусть Хn→ Х0
Тогда Это значит подпоследовательность Теорема доказана.
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 489; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.164.100 (0.01 с.) |



 Замена и знак неравенства меняется на противоположный
Замена и знак неравенства меняется на противоположный зададим произвольное
зададим произвольное  , найдем N, чтобы выполнилось неравенство
, найдем N, чтобы выполнилось неравенство
 Эта функция
Эта функция  целая часть числа
целая часть числа

 покажем, что последовательность не имеет предела (расходится)
покажем, что последовательность не имеет предела (расходится)
 Зададим
Зададим 

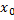 , которое удовлетворяет этим неравенствам одновременно. Это противоречие. Значит, предел этой последовательности не существует, значит, она расходится
, которое удовлетворяет этим неравенствам одновременно. Это противоречие. Значит, предел этой последовательности не существует, значит, она расходится

 ,тогда по определению будет
,тогда по определению будет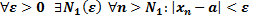



 будут выполняться оба неравенства одновременно, тогда
будут выполняться оба неравенства одновременно, тогда
 - противоречие, двух пределов не может быть
- противоречие, двух пределов не может быть
 - последовательность сходится и
- последовательность сходится и 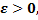 тогда по определению
тогда по определению 





 она ограничена
она ограничена - последовательность ограничена, но она сходится
- последовательность ограничена, но она сходится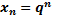 исследовать сходимость последовательности в зависимости от параметра q
исследовать сходимость последовательности в зависимости от параметра q

 найдем N из неравенства
найдем N из неравенства


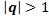

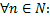


 тогда по определению
тогда по определению 



 и только усилим неравенство
и только усилим неравенство Это будет означать, что последовательность сходится
Это будет означать, что последовательность сходится Х
Х 
 – сходятся, причём
– сходятся, причём 





 имеет предел
имеет предел 
 произвольное число
произвольное число 



 - существуют, это означает, что
- существуют, это означает, что
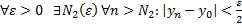

 имеет предел и выполняется равенство Б). Точно так же и для разности
имеет предел и выполняется равенство Б). Точно так же и для разности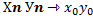
 – сходятся, а значит ограничены
– сходятся, а значит ограничены увеличивая М можно записать неравенство
увеличивая М можно записать неравенство
 тогда
тогда
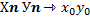


 и последовательность
и последовательность  , то для предела
, то для предела или
или 
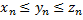 и последовательности
и последовательности  - сходятся к одному и тому же пределу, то
- сходятся к одному и тому же пределу, то
 и докажем
и докажем  тогда по определению для
тогда по определению для

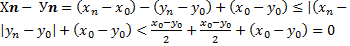
 , что противоречит условию
, что противоречит условию с тремится к а,
с тремится к а, 



 будет выполняться
будет выполняться



 стремится к а
стремится к а
 тогда
тогда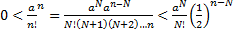




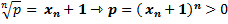




 При
При 
 , тогда если p = 1 то равенство очевидно, а при p
, тогда если p = 1 то равенство очевидно, а при p  надо перейти к обратным числам
надо перейти к обратным числам 

 – бесконечно малая
– бесконечно малая то последовательность
то последовательность  бесконечно малая и наоборот, если
бесконечно малая и наоборот, если  где
где 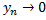 то
то  - бесконечно малая,
- бесконечно малая,  - ограниченная, доказать
- ограниченная, доказать 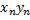 - бесконечно малая
- бесконечно малая

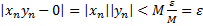
 и последовательность бесконечно малая
и последовательность бесконечно малая
 то
то 

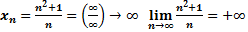

 то последовательность
то последовательность  бесконечно малая
бесконечно малая

 - бесконечно малая
- бесконечно малая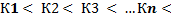 … возрастающая последовательность натуральных чисел
… возрастающая последовательность натуральных чисел называется подпоследовательностью последовательности Хn
называется подпоследовательностью последовательности Хn





