
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема 9. (Лемма о вложенных отрезках)Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть an+1>an, bn+1<bn или тогда существует по меньшей мере одна точка, которая принадлежит всем отрезкам одновременно Доказательство. По условию последовательность an – не убывает, bn – не возрастает, более того обе последовательности an,, bn – ограничены, в силу того a1 Тогда существует предел этих последовательностей
Но по условию теоремы
Таким образом, точки
Теорема 10. (Больцано-Вейерштрасса) Из всякой ограниченной последовательности можно выделить сходящуюся последовательность Доказательство: Пусть Обозначим отрезок Разделим этот отрезок пополам и возьмем ту часть, которая содержит много членов последовательности Обозначим Тогда получим последовательность вложенных отрезков, длина которых равна:
Тогда в силу предыдущей теоремы существует точка Построим последовательность сходящуюся в С, в качестве Таким образом, получили подпоследовательность, которая удовлетворяет неравенству Покажем, что
По теореме сравнения середина тоже стремится к О
Обозначим через Х множество частичных пределов X Очевидно, что Так как множество ограничено, то существует точная нижняя и верхняя грани
Определение 11. Внутренние свойства Последовательность Хn называется фундаментальной, если
То есть это последовательность, у которой члены с увеличением номера n приближаются как угодно близко Теорема 12. Если последовательность Хn – фундаментальная, то она ограничена Доказательство:
Зададим Пусть
Все члены у которого
Обозначим через Это означает, что последовательность ограничена
Теорема 13. Критерий Каши 1. Для того, чтобы последовательность была сходящейся, необходимо и достаточно, чтобы она была фундаментальной Доказательство: Пусть последовательность Хn – сходится и Докажем, что она фундаментальная, то есть выполняется (1), по определению сходящейся последовательности
Достаточность Пусть последовательность фундаментальная, докажем, что она сходится По теореме 12, Хn – ограничена, следовательно из неё можно выделить сходящуюся подпоследовательность Зададим произвольное
Так как По следовательность
(*) Чтобы выполнялось 2 неравенства одновременно, обозначим
Последовательность сходится
§ 2.4 Числовые ряды Пусть { Хn }={ Х1,Х2,Х3 … Хn…} Определение 12. Выражение вида (формально составленной суммы) Х1+Х2+Х3+ … +Хn+…= Называется числовым рядом Sn= Х1+Х2+Х3+ … +Хn= S1= Х1 S2= Х1+Х S3= Х1+Х2+Х3 …….. Частичные суммы сами по себе образуют числовую последовательность, которая называется последовательностью частичных сумм Определение 13. Числовой ряд называется сходящимся, если сходится последовательность его частичных сумм
Предел последовательности частичных сумм называется сумма ряда, записывают Если последовательность Таким образом можно записать
Если ряд сходится Замечание. По определению сходимость ряда (2) равносильна последовательности частичных сумм и наоборот Пусть
Для которого частичной суммой будут члены числовой последовательности и сходимость этой числовой последовательности равна сходимости числового ряда Пример 9 А) исследовать сходимость
Определение 14. Суммы, разности и произведением двух рядов и произведение ряда на число, называются следующие ряды
Теорема 14. Если ряды Доказательство: Обозначим частичные суммы
И рассмотрим ряд
Аналогично теорема доказывается для разности и произведения Замечание. Отбрасывание или добавление конечного числа слагаемых членов ряда не влияет на характер сходимости или расходимости, так как при этом изменится на конечное число частичной суммы. При этом изменится только частичная сумма
Теорема 15. Критерии Каши Для того, чтобы числовой ряд (2) Х1+Х2+Х3+ … +Хn+…=
Доказательство: По определению сходимости ряда равносильно сходится последовательность
Значит, выполняется (3) и наоборот, если выполняется (3), то последовательность
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 461; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.118.164.100 (0.011 с.) |

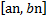 – последовательности вложенных отрезков, то есть
– последовательности вложенных отрезков, то есть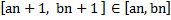
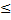 an
an 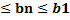 ограничены числами a1 и
ограничены числами a1 и 
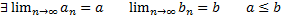 (по теореме Дедекинда)
(по теореме Дедекинда)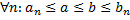
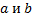 принадлежат всем отрезкам одновременно, в частности они могут и совпадать
принадлежат всем отрезкам одновременно, в частности они могут и совпадать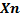 – ограничена
– ограничена 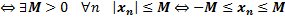

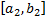 разделим этот отрезок пополам, и обозначим
разделим этот отрезок пополам, и обозначим  и так до
и так до 

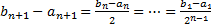
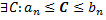 Принадлежащая всем отрезкам одновременно
Принадлежащая всем отрезкам одновременно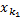 возьмем любой член последовательности
возьмем любой член последовательности  в качестве
в качестве  возьмем
возьмем 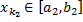 , в качестве
, в качестве  возьмем любой член последовательности
возьмем любой член последовательности 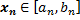

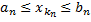
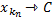 Действительно, что будет выполняться условие
Действительно, что будет выполняться условие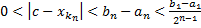
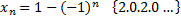 последовательность расходится, не имеет предела, но ограничена и в силу теоремы можно выделить сходящуюся подпоследовательность
последовательность расходится, не имеет предела, но ограничена и в силу теоремы можно выделить сходящуюся подпоследовательность
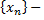 ограниченная последовательность
ограниченная последовательность можно выделить сходящуюся подпоследовательность
можно выделить сходящуюся подпоследовательность
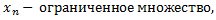 так как все частичные пределы
так как все частичные пределы 
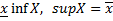 а это множества частичных пределов
а это множества частичных пределов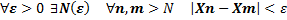 (1)
(1) выполнится (1)
выполнится (1)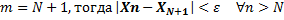
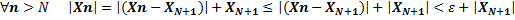
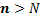

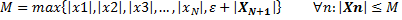
 её предел
её предел тогда
тогда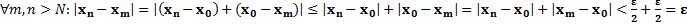 значит выполняется (1) и последовательность будет фундаментальной
значит выполняется (1) и последовательность будет фундаментальной , докажем, что Хn
, докажем, что Хn 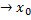 (сходится)
(сходится)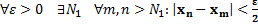
 , получим
, получим 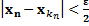
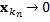 , следовательно
, следовательно
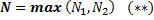
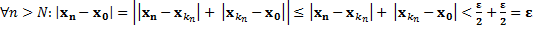
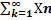 (2)
(2)  - частичная сумма ряда
- частичная сумма ряда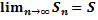 - сумма ряда
- сумма ряда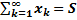
 расходится, то её предел не существует, то говорят, что и ряд расходится
расходится, то её предел не существует, то говорят, что и ряд расходится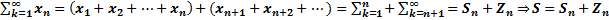
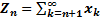
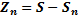
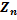 – числовой ряд, который называется остатком исходного числового ряда
– числовой ряд, который называется остатком исходного числового ряда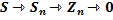
 - некоторая числовая последовательность и составим ряд
- некоторая числовая последовательность и составим ряд

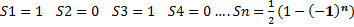
 не существует, этот ряд расходится
не существует, этот ряд расходится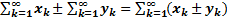
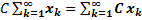
 сходятся, то сходятся их сумма, разность и произведение на число
сходятся, то сходятся их сумма, разность и произведение на число
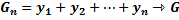


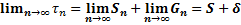

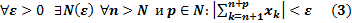
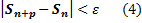 - ясно, что последовательность неравенства равносильно
- ясно, что последовательность неравенства равносильно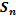 , а сходящаяся последовательность
, а сходящаяся последовательность 
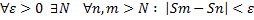
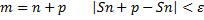
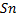 частичных сумм сходится
частичных сумм сходится


