
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Предельные теоремы в схеме Бернулли. Формула Пуассона и условия её применимости.Содержание книги
Поиск на нашем сайте
Формула Бернулли требует громоздких расчетов при большом количестве испытаний. Можно получить более удобную для расчетов приближенную формулу, если при большом числе испытаний вероятность появления А в одном опыте мала, а произведение пр = λ сохраняет постоянное значение для разных серий опытов (то есть среднее число появле-ний события А в разных сериях испытаний остается неизменным). Применим формулу Бернулли:
Найдем предел полученного выражения при
Таким образом, формула Пуассона
позволяет найти вероятность к появлений события А для массовых (п велико) и редких (р мало) событий. Предельные теоремы Предельные теоремы для схем Бернулли  число успехов в последовательности из число успехов в последовательности из  независимых испытаний Бернулли, можно представить в виде: независимых испытаний Бернулли, можно представить в виде:  (1) (1) где  , , где  при больших значениях при больших значениях  . . Это может вызвать значительные вычислительные трудности ввиду громоздкости биномиальных коэффициентов Пуассоновское приближение Верна следущая предельная теорема: Теорема Пуассона: Пусть , ,  таким образом, что таким образом, что  , где , где  - заданное число. Тогда для любого фиксированного - заданное число. Тогда для любого фиксированного   .Другими словами, в описанном предельном переходе биномиальные вероятности .Другими словами, в описанном предельном переходе биномиальные вероятности  аппроксимируются пуассоновским распределением. Доказательство: аппроксимируются пуассоновским распределением. Доказательство: Для краткости будем считать, что  , , поскольку выражение в квадратных скобках стремится к единице, если Нормальное приближение  , а вероятность успеха в единичном испытании , а вероятность успеха в единичном испытании  остается фиксированной. остается фиксированной. Верна так называемая интегральная теорема Муавра-Лапласа. Теорема Муавра-Лапласа: Пусть - число успехов в последовательности из - число успехов в последовательности из  независимых испытаний Бернулли с вероятностью успеха в единичном испытании независимых испытаний Бернулли с вероятностью успеха в единичном испытании  . Пусть . Пусть  . При . При   (2), (2), где Замечание 1. Функция , появившаяся в этой теореме, называется функцией распределения стандартного нормального закона. , появившаяся в этой теореме, называется функцией распределения стандартного нормального закона. Дл язначений этой функции существуют подробные таблицы. Отметим, что она не зависит ни от каких параметров. Следовательно, предел в теореме Муавра-Лапласа является универсальным, так как он не зависит от параметра Замечание 2. Чтобы понять смысл выражения (3), (3), необходимо вспомнить, что  . . Замечание 3. В предельном переходе " , " , "  фиксировано" фиксировано" каждая "индивидуальная" вероятность
таким образом, в последней сумме содержится много (порядка Замечание 4. Скорость сходимости в (2) хорошо изучена. Имеет место так называемая оценка Берри-Эссеена:Существует такое  . .
О применимости предельных теорем в схеме Бернулли 1.Если 2.Если На практике в ситуации, когда
|
||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 1054; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.009 с.) |




 (3.4)
(3.4)
 - независимые одинаково распределенные бернуллиевские случайные величины. Мы знаем в явном виде распределение
- независимые одинаково распределенные бернуллиевские случайные величины. Мы знаем в явном виде распределение  и необходимости возводить числа
и необходимости возводить числа  в высокие степени. Ниже мы рассмотрим две важные предельные ситуации, когда биномиальное распределение может быть приближено другими распределениями.
в высокие степени. Ниже мы рассмотрим две важные предельные ситуации, когда биномиальное распределение может быть приближено другими распределениями.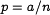 .Тогда
.Тогда .
. и
и  . Таким образом, это выражение имеет вид
. Таким образом, это выражение имеет вид  . Легко видеть, что
. Легко видеть, что  , а
, а  .
. ,
, ) слагаемых.
) слагаемых. , что
, что не велико, следует пользоваться пуассоновским приближением;
не велико, следует пользоваться пуассоновским приближением; велико, то можно применять нормальное приближение.
велико, то можно применять нормальное приближение. , то применяют пуассоновское приближение; если же
, то применяют пуассоновское приближение; если же 


