Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Корреляционный момент. Коэффициент корреляции. Свойства ковариации и коэффициента корреляции.Содержание книги
Поиск на нашем сайте
Коэффициентом ковариации называется выражение: cov(X,Y)=M[(X-MX)(Y-MY)]=M[XY-XMY-YMX+MX•MY]=MXY-2MX•MY+MX•MY=MXY-MX•MY Если случайные величины XY независимы, то их коэффициент ковариации равен нулю, обратное в общем случае неверно. Коэффициентом корреляции случайных величин X и Y называется число:
X*=(X-MX)/σx D(X±Y)=M[X±Y-M(X±Y)]2=M[X±Y-MX∓MY]2=M[(X-MX)±(Y-MY)]2=M[(M-MX)2±2(X-MX)(Y-MY)+(Y-MY)2]=M(X_MX)2±2M(X-MX)(Y-MY)+M(Y-MY)2=DX±cov(XY)+DY Следствие: Если X и Y независимы, то коэффициент ковариации равен 0 и следовательно D(X±Y)=DX±DY Свойства коэффициента корреляции 1. -1≤pxy≤1
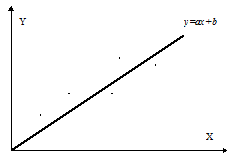
В общем случае Y можно представить в виде y=ax+b+z DZ=σy2(1-pxy)2 Коэффициент корреляции является мерой близости линейной связи между случайными величинами X и Y: чем ближе коэффициент корреляции по модулю к 1, тем более тесно результаты конкретного испытания над X и Y соотносятся с прямой ax+b. Свойства ковариации § Ковариация симметрична:
§ В силу линейности математического ожидания, ковариация может быть записана как
§ Пусть
В частности ковариация (в отличие от коэффициента корреляции) не инварианта относительно смены масштаба, что не всегда удобно в приложениях. § Ковариация случайной величины с собой равна дисперсии:
§ Если
Обратное, вообще говоря, неверно. § Неравенство Коши — Буняковского:
Предельные теоремы теории вероятностей. Неравенство и теория Чебышева
Неравенство Чебышева. Неравенство Чебышева, используемое для доказательства дальнейших теорем, справед-ливо как для непрерывных, так и для дискретных случайных величин. Докажем его для дискретных случайных величин.
Теорема 13.1(неравенство Чебышева). p( | X – M (X)| < ε) ≥ D (X) / ε². (13.1) Доказательство. Пусть Х задается рядом распределения
Так как события | X – M (X)| < ε и | X – M (X)| ≥ ε противоположны, то р (| X – M (X)| < ε) + + р (| X – M (X)| ≥ ε) = 1, следовательно, р (| X – M (X)| < ε) = 1 - р (| X – M (X)| ≥ ε). Найдем р (| X – M (X)| ≥ ε). D (X) = (x 1 – M (X))² p 1 + (x 2 – M (X))² p 2 + … + (xn – M (X))² pn. Исключим из этой суммы те слагаемые, для которых | X – M (X)| < ε. При этом сумма может только уменьшиться, так как все входящие в нее слагаемые неотрицательны. Для определенности будем считать, что отброшены первые k слагаемых. Тогда
D (X) ≥ (xk+ 1 – M (X))² pk+ 1 + (xk+ 2 – M (X))² pk +2 + … + (xn – M (X))² pn ≥ ε² (pk+ 1 + pk+ 2 + … + pn). Отметим, что pk+ 1 + pk+ 2 + … + pn есть вероятность того, что | X – M (X)| ≥ ε, так как это сумма вероятностей всех возможных значений Х, для которых это неравенство справедливо. Следовательно, D (X) ≥ ε² р (| X – M (X)| ≥ ε), или р (| X – M (X)| ≥ ε) ≤ D (X) / ε². Тогда вероятность противоположного события p( | X – M (X)| < ε) ≥ D (X) / ε², что и требо-валось доказать.
|
|||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 496; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.138.102.219 (0.01 с.) |


 Править
Править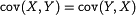 .
. .
.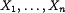 случайные величины, а
случайные величины, а 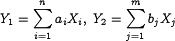 их две произвольные линейные комбинации. Тогда
их две произвольные линейные комбинации. Тогда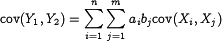 .
.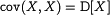 .
.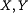 независимые случайные величины, то
независимые случайные величины, то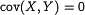 .
.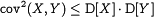 .
.