
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Центральная предельная теорема.Содержание книги
Поиск на нашем сайте
Рассмотрим одну из наиболее общих форм центральной предельной теоремы: Пусть имеется взвешенная сумма независимых случайных непрерывных величин x1, x2, x3, …., xn с произвольными законами распределения:
Пусть i-ая случайная величина имеет Согласно теореме о числовых характеристиках случайных величин, получим:
Центральная предельная теорема утверждает, что при достаточно общих условиях распределения суммарной Yn при
Опыт показывает, что когда
Математическая статистика. Основные понятия. Математическая статистика занимается установлением закономерностей, которым подчинены массовые случайные явления, на основе обработки статистических данных, полученных в результате наблюдений. Двумя основными задачами математической статистики являются: - определение способов сбора и группировки этих статистических данных; - разработка методов анализа полученных данных в зависимости от целей исследования, к которым относятся: а) оценка неизвестной вероятности события; оценка неизвестной функции распределения; оценка параметров распределения, вид которого известен; оценка зависимости от других случайных величин и т.д.; б) проверка статистических гипотез о виде неизвестного распределения или о значениях параметров известного распределения. Для решения этих задач необходимо выбрать из большой совокупности однородных объектов ограниченное количество объектов, по результатам изучения которых можно сделать прогноз относительно исследуемого признака этих объектов. Определим основные понятия математической статистики. Генеральная совокупность – все множество имеющихся объектов. Выборка – набор объектов, случайно отобранных из генеральной совокупности. Объем генеральной совокупности N и объем выборки n – число объектов в рассматривае-мой совокупности. Виды выборки: Повторная – каждый отобранный объект перед выбором следующего возвращается в генеральную совокупность; Бесповторная – отобранный объект в генеральную совокупность не возвращается.
Пусть интересующая нас случайная величина Х принимает в выборке значение х 1 п 1 раз, х 2 – п 2 раз, …, хк – пк раз, причем
Если исследуется некоторый непрерывный признак, то вариационный ряд может состоять из очень большого количества чисел. В этом случае удобнее использовать группированную выборку. Для ее получения интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько равных частичных интервалов длиной h, а затем находят для каждого частичного интервала ni – сумму частот вариант, попавших в i -й интервал. Составленная по этим результатам таблица называется группированным статистическим рядом:
|
||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 399; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.135.214.175 (0.005 с.) |

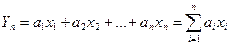 , где
, где 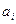 постоянная, фиксированная числа.
постоянная, фиксированная числа.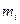 и
и 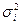 (i=1,2,3,…,n-1,n)
(i=1,2,3,…,n-1,n)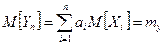
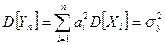
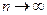 стремиться к нормальному распределению
стремиться к нормальному распределению 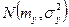
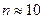 или меньше, то закон распределения суммы может быть заменен нормальным.
или меньше, то закон распределения суммы может быть заменен нормальным.

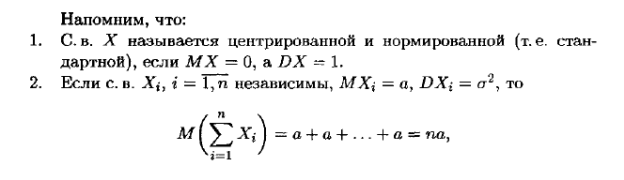
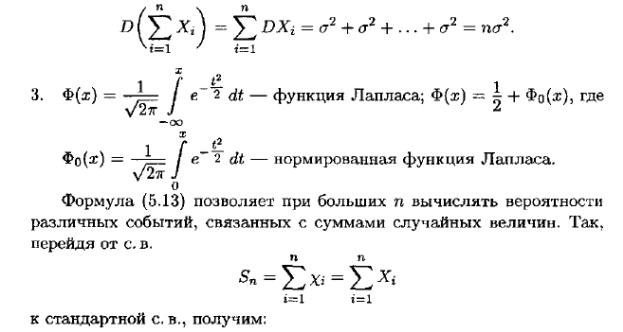

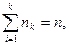 где п – объем выборки. Тогда наблюдаемые значения случайной величины х 1, х 2,…, хк называют вариантами, а п 1, п 2,…, пк – частотами. Если разделить каждую частоту на объем выборки, то получим относительные частоты
где п – объем выборки. Тогда наблюдаемые значения случайной величины х 1, х 2,…, хк называют вариантами, а п 1, п 2,…, пк – частотами. Если разделить каждую частоту на объем выборки, то получим относительные частоты 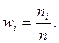 Последовательность вариант, записанных в порядке возрастания, называют вариационным рядом, а перечень вариант и соответствующих им частот или относительных частот – стати-стическим рядом:
Последовательность вариант, записанных в порядке возрастания, называют вариационным рядом, а перечень вариант и соответствующих им частот или относительных частот – стати-стическим рядом:


