
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Элементы комбинаторики. Схемы выбора без возвращения и с возвращением.Содержание книги
Поиск на нашем сайте
При вычислении вероятностей часто приходится использовать некоторые формулы комбинаторики – науки, изучающей комбинации, которые можно составить по определенным правилам из элементов некоторого конечного множества. Определим основные такие комбинации.
Перестановки – это комбинации, составленные из всех п элементов данного множества и отличающиеся только порядком их расположения. Число всех возможных перестановок Рп = п!
Размещения – комбинации из т элементов множества, содержащего п различных элементов, отличающиеся либо составом элементов, либо их порядком. Число всех возможных размещений
Сочетания – неупорядоченные наборы из т элементов множества, содержащего п различных элементов (то есть наборы, отличающиеся только составом элементов). Число сочетаний
Урны и шарики Есть урна (то есть ящик), содержащая Рассмотрим следующие возможные схемы выбора: 1. Выбор с возвращением: каждый выбранный шарик возвращается в урну, то есть каждый из 2. Выбор без возвращения: выбранные шарики в урну не возвращаются, и в полученном наборе не могут встречаться одни и те же номера (выборка без повторений). И в том, и в другом случае результатом выбора является набор из 1. Выбор с учетом порядка: два набора номеров шариков считаются различными, если они отличаются составом или порядком номеров. Так, при выборе трех шариков из урны, содержащей 5 шариков, наборы 2. Выбор без учета порядка: два набора номеров шариков считаются различными, если они отличаются составом. Наборы, отличающиеся лишь порядком следования номеров, считаются одинаковыми. Так, в примере выше первые два набора Подсчитаем теперь, сколько же возможно различных результатов при каждой из четырех схем (выбор с возвращением и без, и в каждом из этих случаев учитываем ли мы порядок или нет).
|
||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 818; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.007 с.) |

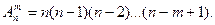 (1.4)
(1.4)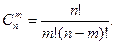 (1.5)
(1.5) занумерованных объектов, которые мы без ограничения общности будем считать шариками. Мы выбираем из этой урны
занумерованных объектов, которые мы без ограничения общности будем считать шариками. Мы выбираем из этой урны  шариков. Нас интересует, сколькими способами можно выбрать
шариков. Нас интересует, сколькими способами можно выбрать 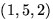 ,
,  и
и 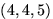 различны, если производится выбор с учетом порядка.
различны, если производится выбор с учетом порядка.


