
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Математическое ожидание и дисперсия числа появления события в независимых опытах.Содержание книги
Поиск на нашем сайте Определение. Математическим ожиданием непрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл
Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:
Математическим ожиданием дискретной случайной величины называется сумма произведений ее возможных значений на соответствующие им вероятности: М (Х) = х 1 р 1 + х 2 р 2 + … + хпрп. (7.1) Если число возможных значений случайной величины бесконечно, то Замечание 1. Математическое ожидание называют иногда взвешенным средним, так как оно приближенно равно среднему арифметическому наблюдаемых значений случайной величины при большом числе опытов. Замечание 2. Из определения математического ожидания следует, что его значение не меньше наименьшего возможного значения случайной величины и не больше наибольшего. Замечание 3. Математическое ожидание дискретной случайной величины есть неслучай-ная (постоянная) величина. В дальнейшем увидим, что это же справедливо и для непре-рывных случайных величин.
Свойства математического ожидания. 3) Математическое ожидание постоянной равно самой постоянной: М (С) = С. (7.2) Доказательство. Если рассматривать С как дискретную случайную величину, принимающую только одно значение С с вероятностью р = 1, то М (С) = С ·1 = С. 4) Постоянный множитель можно выносит за знак математического ожидания: М (СХ) = С М (Х). (7.3) Доказательство. Если случайная величина Х задана рядом распределения
то ряд распределения для СХ имеет вид:
Тогда М (СХ) = Сх 1 р 1 + Сх 2 р 2 + … + Схпрп = С (х 1 р 1 + х 2 р 2 + … + хпрп) = СМ (Х).
Математическим ожиданием непрерывной случайной величины называется
Замечание 1. Общее определение дисперсии сохраняется для непрерывной случайной величины таким же, как и для дискретной (опр. 7.5), а формула для ее вычисления имеет вид:
Среднее квадратическое отклонение вычисляется по формуле (7.12). Замечание 2. Если все возможные значения непрерывной случайной величины не выходят за пределы интервала [ a, b ], то интегралы в формулах (7.13) и (7.14) вычисляются в этих пределах. Теорема. Дисперсия числа появлений события Доказательство. Пусть Но Как было показано выше, Тогда В этом случае, как уже упоминалось ранее, среднее квадратичное отклонение
|
||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 441; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.008 с.) |


 При этом, конечно, предполагается, что несобственный интеграл сходится.
При этом, конечно, предполагается, что несобственный интеграл сходится.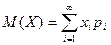 , если полученный ряд сходится абсолютно.
, если полученный ряд сходится абсолютно.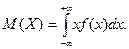 (7.13)
(7.13) (7.14)
(7.14) в
в 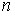 независимых испытаниях равна произведению числа испытаний на вероятности появления и непоявления события
независимых испытаниях равна произведению числа испытаний на вероятности появления и непоявления события 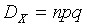 .
. – число появлений события
– число появлений события  . Так как испытания независимы, то и случайные величины
. Так как испытания независимы, то и случайные величины 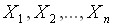 – независимы, поэтому
– независимы, поэтому 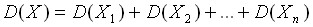 .
. ,
, 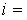
 .
. , а
, а  .
.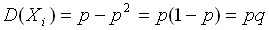 , а
, а 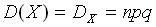 .
. .
.


