Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Зависимость и независимость двух случайных величин. Числовые характеристики двумерной с.в. Математическое ожидание и дисперсия.Содержание книги
Поиск на нашем сайте
Распределения соответствующих компонент в одной и другой таблицах одинаковы. Однако очевидно, что эти таблицы описывают абсолютно различные распределения двумерного случайного вектора Таким образом, на поставленный выше вопрос можно дать следующий ответ: «Зная законы распределения отдельных случайных величин X и Y, входящих в систему, найти закон распределения всей системы в общем случае нельзя». Заметим, что это можно сделать только в одном частном случае, когда случайные величины X и Y, образующие систему, независимы. Определение. Две случайные величины X и Y называются независимыми, если независимы все связанные с ними события. Например, Замечание. Так как зависимость и независимость событий всегда взаимны (если событие A не зависит от события B, то и событие B не зависит от события A), поэтому зависимость и независимость случайных величин также всегда взаимны: если случайная величина X не зависит от случайной величины Y, то Y не зависит от X. В терминах законов распределения независимость случайных величин можно определить так: «Две случайные величины называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая». Если компоненты X и Y двумерного вектора Верно и обратное утверждение. Это правило является необходимым и достаточным условием независимости для случайных величин любого типа. Необходимые и достаточные условия независимости компонент X и Y для дискретного и непрерывного случаев: 1. X и Y являются независимыми дискретными случайными величинами тогда и только тогда, когда для всех значений индексов i и j выполняется 2. X и Y являются независимыми непрерывными случайными величинами тогда и только тогда, когда Отметим, что допускается нарушение последнего равенства на множестве точек Ответ: компоненты X и Y независимы. Замечание. В данном случае независимость компонент X и Y можно было установить, внимательно посмотрев на исходную таблицу, задающую закон распределения случайного вектора
Числовые характеристики двумерных случайных величин. Def: математическим ожиданием составляющей
Математическим ожиданием составляющей
Def: математическим ожиданием составляющей
В результате получим:
Математическим ожиданием составляющей
Def: дисперсией составляющей
Дисперсией составляющей
Def: дисперсией составляющей
дисперсией составляющей
Корни квадратные из дисперсии называют средними квадратичными отклонениями составляющих:
Корреляционный момент (ковариация).
|
|||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 421; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.66.200 (0.008 с.) |

 (все значения
(все значения  в одной таблице отличны от соответствующих значений
в одной таблице отличны от соответствующих значений  и
и  ;
;  и
и  и т.д.
и т.д. выражается, через функции распределения отдельных компонент:
выражается, через функции распределения отдельных компонент: .
. .
. .
. , имеющих двумерную площадь, равную нулю.
, имеющих двумерную площадь, равную нулю. двумерной дискретной случайной величины
двумерной дискретной случайной величины  называют число:
называют число:
 двумерной дискретной случайной величины
двумерной дискретной случайной величины 
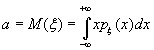 , где
, где