
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Генеральная совокупность и выборка. Характеристики выборки. Способы отбора.Содержание книги
Поиск на нашем сайте
Генеральная совокупность – все множество имеющихся объектов. Выборка – набор объектов, случайно отобранных из генеральной совокупности.
В матем статистике понятие генеральной совокупности трактуется как совокупность всех мыслимых наблюдений, которые могли бы быть произведены при данном реальном комплексе условий. Иначе, совокупность объектов, из которых произведена выборка.ё ё Выборочная совокупность -совокупность случайно отобранных объектов. Выборочный метод обследования, или как его часто называют, выборка, применяется, прежде всего, в тех случаях, когда сплошное наблюдение вообще невозможно. Виды выборки: вероятностные и невероятностные. Вероятностная выборка: 1. Простая вероятностная выборка: - простая повторная выборка. Использование такой выборки основывается на предположении, что каждый респондент с равной долей вероятности может попасть в выборку. - простая бесповторная выборка. 2. Систематическая вероятностная выборка. Является упрощенным вариантом простой вероятностной выборки. 3. Серийная вероятностная выборка. 4. Районированные выборки 5. «Удобная» выборка Процедура «удобной» выборки состоит в установлении контактов с «удобными» единицами выборки. Невероятностные выборка (отбор в такой выборке осуществляется не по принципам случайности, а по субъективным критериям- доступности, типичности, равного представительства и т.д.: 1.Квотная выборка- выборка строится как модель, которая воспроизводит структуру генеральной совокупности в виде квот изучаемых признаков. 2. Метод снежного кома. 3. Стихийная выборка. Способы отбора: 1.Рандомизация или случайный отбор, используется для создания случайных выборок. 2.Попарный отбор- стратегия построения групп выборки, при котором составляются из субъектов, эквивалентных по значимым для эксперимента побочным параметрам. 3.Многоступенчатый способ построения выборки. При многоступенчатом отборе выборка строится в несколько этапов, причём на каждой стадии меняется единица отбора. 4..Многосфазный способ построения выборки.- является разновидностью многоступенчатого способа, заключается в том, что из сформированной выборки большего объёма производится новая выборка меньшего объёма, при этом, единица отбора остаётся одной и той же.
5.Комбинированный способ построения выборки- соединение в многоступенчатой выборке различных приёмов отбора. Статистическое распределение выборки.
Эмпирическая функция распределения.
Полигон и гистограмма. Для наглядного представления о поведении исследуемой случайной величины в выборке можно строить различные графики. Один из них – полигон частот: ломаная, отрезки которой соединяют точки с координатами (x 1, n 1), (x 2, n 2),…, (xk, nk), где xi откладываются на оси абсцисс, а ni – на оси ординат. Если на оси ординат откладывать не абсолютные (ni), а относительные (wi) частоты, то получим полигон относительных частот (рис.1). По аналогии с функцией распределения случайной величины можно задать некоторую функцию, относительную частоту события X < x. Определение 15.1. Выборочной (эмпирической) функцией распределения называют функцию F* (x), определяющую для каждого значения х относительную частоту события X < x. Таким образом,
где пх – число вариант, меньших х, п – объем выборки.
Замечание. В отличие от эмпирической функции распределения, найденной опытным путем, функцию распределения F (x) генеральной совокупности называют теоретической функцией распределения. F (x) определяет вероятность события X < x, а F* (x) – его относительную частоту. При достаточно больших п, как следует из теоремы Бернулли, F* (x) стремится по вероятности к F (x). Из определения эмпирической функции распределения видно, что ее свойства совпадают со свойствами F (x), а именно: 1) 0 ≤ F* (x) ≤ 1. 2) F* (x) – неубывающая функция. 3) Если х 1 – наименьшая варианта, то F* (x) = 0 при х ≤ х 1; если хк – наибольшая варианта, то F* (x) = 1 при х > хк. Для непрерывного признака графической иллюстрацией служит гистограмма, то есть ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длиной h, а высотами – отрезки длиной ni /h (гистограмма частот) или wi /h (гистограмма относительных частот). В первом случае площадь гистограммы равна объему выборки, во втором – единице (рис.2).
|
|||||
|
Последнее изменение этой страницы: 2016-12-27; просмотров: 412; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.218.149.167 (0.007 с.) |






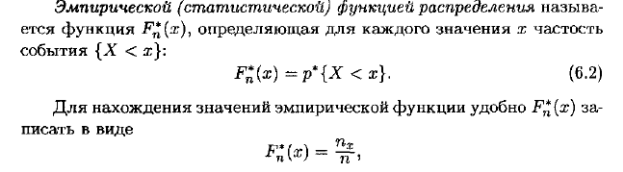


 Рис. 1.
Рис. 1. , (15.1)
, (15.1) Рис.2.
Рис.2.


