
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Вопрос 2. Теорема умножения вероятностейСодержание книги Поиск на нашем сайте
Оглавление Вопрос 1. Метод моментов. 2 Вопрос 2. Теорема умножения вероятностей. 3 Вопрос 3. Понятие начального и центрального моментов. 5 Вопрос 4. Понятие генеральной и выборочной совокупности. 6 Вопрос 5. Оценка числовых характеристик. 9 Вопрос 6. Показательный закон распределения и его свойства. 14 Вопрос 7. Формула Байеса (теорема гипотез) 15 Вопрос 8. Математическое ожидание и его свойства. 16 Вопрос 9. Условный закон распределения двумерной случайной величины.. 19 Вопрос 10. Теорема умножения независимых событий. 21 Вопрос 11. Неравенство Чебышева. 22 Вопрос 12. Классификация событий. 24 Вопрос 13. Нормальный закон распределения и его свойства. 25 Вопрос 14. Равномерный закон и его свойства. 27 Свойства плотности распределения. 27 Равномерный закон распределения. 28 Вопрос 15. Центральная предельная теорема. 30 Характеристические функции. 30 Свойства характеристических функций. 30 Вопрос 16. Метод максимального правдоподобия. 34 Способы построения оценок. 35 1. Метод наибольшего правдоподобия. 35 2. Метод моментов. 36 3. Метод наименьших квадратов. 36 4. Байесовский подход к получению оценок. 37 Вопрос 17. Закон больших чисел. 38 Неравенство Чебышева. 38 Теоремы Чебышева и Бернулли. 38 Вопрос 18. Основные свойства плотностей и интегральных плотностей. 41 Вопрос 19. Дисперсия, мода, медиана и их свойства. 41 Мода и медиана. 41 Асимметрия и эксцесс. 42 Числовые характеристики двумерных случайных величин. 43 Корреляционный момент и коэффициент корреляции. 44 Вопрос 20. Основные свойства оценок. 46 Вопрос 21. Вероятности. Условная вероятность. 46 Теорема сложения вероятностей. 47 Теорема умножения вероятностей (условные вероятности). 49 Вероятность появления хотя бы одного события. 51 Вопрос 22. Оценка дисперсии, Гистограмма. 52 ПО ОЦЕНКЕ ДИСПЕРСИИ СМ вопрос № 16! 52 Первичная обработка результатов. 53 Полигон частот. Выборочная функция распределения и гистограмма. 54 Примеры построения гистограмм. 55 Вопрос 23. Полная вероятность. 57 Вопрос 24. Числовые характеристики случайных величин, коэффициент корреляции. 57 Вопрос 25. Понятие случайной величины. 57 Случайные величины.. 57 Дискретные и непрерывные случайные величины.. 57
Вопрос 1. Метод моментов Метод моментов основан на том, что начальные и центральные эмпирические моменты являются состоятельными оценками соответственно начальных и центральных теоретических моментов, поэтому можно приравнять теоретические моменты соответствующим эмпирическим моментам того же порядка.
Если задан вид плотности распределения f (x, Θ), определяемой одним неизвестным параметром Θ, то для оценки этого параметра достаточно иметь одно уравнение. Например, можно приравнять начальные моменты первого порядка:
получив тем самым уравнение для определения Θ. Его решение Θ* будет точечной оценкой параметра, которая является функцией от выборочного среднего и, следовательно, и от вариант выборки: Θ = ψ (х 1, х 2, …, хп). Если известный вид плотности распределения f (x, Θ1, Θ2) определяется двумя неизвестными параметрами Θ1 и Θ2, то требуется составить два уравнения, например ν1 = М 1, μ2 = т 2. Отсюда Θ1 = ψ1 (х 1, х 2, …, хп), Θ2 = ψ2(х 1, х 2, …, хп).
Вопрос 3. Понятие начального и центрального моментов Определение 9.1. Начальным моментом порядка k случайной величины Х называется математическое ожидание величины Xk: ν k = M (Xk). (9.1) В частности, ν1 = М (Х), ν2 = М (Х 2). Следовательно, дисперсия D (X) = ν2 – ν1². Определение 9.2. Центральным моментом порядка k случайной величины Х называется математическое ожидание величины (Х – М (Х)) k: μ k = M ((Х – М (Х)) k). (9.2) В частности, μ1 = M (Х – М (Х)) = 0, μ2 = M ((Х – М (Х))2) = D (X). Можно получить соотношения, связывающие начальные и центральные моменты:
Вопрос 5. Оценка числовых характеристик
Закон распределения (функция распределения и ряд распределения или плотность вероятности) полностью описывают поведение случайной величины. Но в ряде задач достаточно знать некоторые числовые характеристики исследуемой величины (например, ее среднее значение и возможное отклонение от него), чтобы ответить на поставленный вопрос. Рассмотрим основные числовые характеристики дискретных случайных величин.
Математическое ожидание
Определение 7.1. Математическим ожиданием дискретной случайной величины называется сумма произведений ее возможных значений на соответствующие им вероятности:
М (Х) = х 1 р 1 + х 2 р 2 + … + хпрп. (7.1) Если число возможных значений случайной величины бесконечно, то Замечание 1. Математическое ожидание называют иногда взвешенным средним, так как оно приближенно равно среднему арифметическому наблюдаемых значений случайной величины при большом числе опытов. Замечание 2. Из определения математического ожидания следует, что его значение не меньше наименьшего возможного значения случайной величины и не больше наибольшего. Замечание 3. Математическое ожидание дискретной случайной величины есть неслучайная (постоянная) величина. В дальнейшем увидим, что это же справедливо и для непрерывных случайных величин.
Пример 1. Найдем математическое ожидание случайной величины Х – числа стандартных деталей среди трех, отобранных из партии в 10 деталей, среди которых 2 бракованных. Составим ряд распределения для Х. Из условия задачи следует, что Х может принимать значения 1, 2, 3.
Пример 2. Определим математическое ожидание случайной величины Х – числа бросков монеты до первого появления герба. Эта величина может принимать бесконечное число значений (множество возможных значений есть множество натуральных чисел). Ряд ее распределения имеет вид:
Тогда
+ Свойства математического ожидания. 1) Математическое ожидание постоянной равно самой постоянной: М (С) = С. (7.2) Доказательство. Если рассматривать С как дискретную случайную величину, принимающую только одно значение С с вероятностью р = 1, то М (С) = С ·1 = С. 2) Постоянный множитель можно выносит за знак математического ожидания: М (СХ) = С М (Х). (7.3) Доказательство. Если случайная величина Х задана рядом распределения
то ряд распределения для СХ имеет вид:
Тогда М (СХ) = Сх 1 р 1 + Сх 2 р 2 + … + Схпрп = С (х 1 р 1 + х 2 р 2 + … + хпрп) = СМ (Х). Определение 7.2. Две случайные величины называются независимыми, если закон распределения одной из них не зависит от того, какие значения приняла другая. В противном случае случайные величины зависимы. Определение 7.3. Назовем произведением независимых случайных величин Х и Y случайную величину XY, возможные значения которой равны произведениям всех возможных значений Х на все возможные значения Y, а соответствующие им вероят-ности равны произведениям вероятностей сомножителей. 3) Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий: M (XY) = M (X) M (Y). (7.4) Доказательство. Для упрощения вычислений ограничимся случаем, когда Х и Y принимают только по два возможных значения:
Тогда ряд распределения для XY выглядит так:
Следовательно, M (XY) = x 1 y 1· p 1 g 1 + x 2 y 1· p 2 g 1 + x 1 y 2· p 1 g 2 + x 2 y 2· p 2 g 2 = y 1 g 1(x 1 p 1 + x 2 p 2) + + y 2 g 2(x 1 p 1 + x 2 p 2) = (y 1 g 1 + y 2 g 2) (x 1 p 1 + x 2 p 2) = M (X)· M (Y). Замечание 1. Аналогично можно доказать это свойство для большего количества возможных значений сомножителей.
Замечание 2. Свойство 3 справедливо для произведения любого числа независимых случайных величин, что доказывается методом математической индукции. Определение 7.4. Определим сумму случайных величин Х и Y как случайную величину Х +Y, возможные значения которой равны суммам каждого возможного значения Х с каждым возможным значением Y; вероятности таких сумм равны произведениям вероятностей слагаемых (для зависимых случайных величин – произведениям вероятности одного слагаемого на условную вероятность второго). 4) Математическое ожидание суммы двух случайных величин (зависимых или незави-симых) равно сумме математических ожиданий слагаемых: M (X + Y) = M (X) + M (Y). (7.5) Доказательство. Вновь рассмотрим случайные величины, заданные рядами распределения, приведен-ными при доказательстве свойства 3. Тогда возможными значениями X + Y являются х 1 + у 1, х 1 + у 2, х 2 + у 1, х 2 + у 2. Обозначим их вероятности соответственно как р 11, р 12, р 21 и р 22. Найдем М (Х + Y) = (x 1 + y 1) p 11 + (x 1 + y 2) p 12 + (x 2 + y 1) p 21 + (x 2 + y 2) p 22 = = x 1(p 11 + p 12) + x 2(p 21 + p 22) + y 1(p 11 + p 21) + y 2(p 12 + p 22). Докажем, что р 11 + р 22 = р 1. Действительно, событие, состоящее в том, что X + Y примет значения х 1 + у 1 или х 1 + у 2 и вероятность которого равна р 11 + р 22, совпадает с событием, заключающемся в том, что Х = х 1 (его вероятность – р 1). Аналогично дока-зывается, что p 21 + p 22= р 2, p 11 + p 21 = g 1, p 12 + p 22 = g 2. Значит, M (X + Y) = x 1 p 1 + x 2 p 2 + y 1 g 1 + y 2 g 2 = M (X) + M (Y). Замечание. Из свойства 4 следует, что сумма любого числа случайных величин равна сумме математических ожиданий слагаемых. Пример. Найти математическое ожидание суммы числа очков, выпавших при броске пяти игральных костей. Найдем математическое ожидание числа очков, выпавших при броске одной кости: М (Х 1) = (1 + 2 + 3 + 4 + 5 + 6)
Дисперсия. Для того, чтобы иметь представление о поведении случайной величины, недостаточно знать только ее математическое ожидание. Рассмотрим две случайные величины: Х и Y, заданные рядами распределения вида
Найдем М (Х) = 49·0,1 + 50·0,8 + 51·0,1 = 50, М (Y) = 0·0,5 + 100·0,5 = 50. Как видно, математические ожидания обеих величин равны, но если для Х М (Х) хорошо описывает поведение случайной величины, являясь ее наиболее вероятным возможным значением (причем остальные значения ненамного отличаются от 50), то значения Y существенно отстоят от М (Y). Следовательно, наряду с математическим ожиданием желательно знать, насколько значения случайной величины отклоняются от него. Для характеристики этого показателя служит дисперсия.
Определение 7.5. Дисперсией (рассеянием) случайной величины называется математическое ожидание квадрата ее отклонения от ее математического ожидания: D (X) = M (X – M (X))². (7.6) Пример. Найдем дисперсию случайной величины Х (числа стандартных деталей среди отобранных) в примере 1 данной лекции. Вычислим значения квадрата отклонения каждого возможного значения от математического ожидания: (1 – 2,4)2 = 1,96; (2 – 2,4)2 = 0,16; (3 – 2,4)2 = 0,36. Следовательно,
Замечание 1. В определении дисперсии оценивается не само отклонение от среднего, а его квадрат. Это сделано для того, чтобы отклонения разных знаков не компенсировали друг друга. Замечание 2. Из определения дисперсии следует, что эта величина принимает только неотрицательные значения. Замечание 3. Существует более удобная для расчетов формула для вычисления дисперсии, справедливость которой доказывается в следующей теореме: Теорема 7.1. D (X) = M (X ²) – M ²(X). (7.7) Доказательство. Используя то, что М (Х) – постоянная величина, и свойства математического ожидания, преобразуем формулу (7.6) к виду: D (X) = M (X – M (X))² = M (X ² - 2 X·M (X) + M ²(X)) = M (X ²) – 2 M (X)· M (X) + M ²(X) = = M (X ²) – 2 M ²(X) + M ²(X) = M (X ²) – M ²(X), что и требовалось доказать. Пример. Вычислим дисперсии случайных величин Х и Y, рассмотренных в начале этого раздела. М (Х) = (492·0,1 + 502·0,8 + 512·0,1) – 502 = 2500,2 – 2500 = 0,2. М (Y) = (02·0,5 + 100²·0,5) – 50² = 5000 – 2500 = 2500. Итак, дисперсия второй случайной величины в несколько тысяч раз больше дисперсии первой. Таким образом, даже не зная законов распределения этих величин, по известным значениям дисперсии мы можем утверждать, что Х мало отклоняется от своего математического ожидания, в то время как для Y это отклонение весьма существенно. Свойства дисперсии. 1) Дисперсия постоянной величины С равна нулю: D (C) = 0. (7.8) Доказательство. D (C) = M ((C – M (C))²) = M ((C – C)²) = M (0) = 0. 2) Постоянный множитель можно выносить за знак дисперсии, возведя его в квадрат: D (CX) = C ² D (X). (7.9) Доказательство. D (CX) = M ((CX – M (CX))²) = M ((CX – CM (X))²) = M (C ²(X – M (X))²) = = C ² D (X). 3) Дисперсия суммы двух независимых случайных величин равна сумме их дисперсий: D (X + Y) = D (X) + D (Y). (7.10) Доказательство. D (X + Y) = M (X ² + 2 XY + Y ²) – (M (X) + M (Y))² = M (X ²) + 2 M (X) M (Y) + + M (Y ²) – M ²(X) – 2 M (X) M (Y) – M ²(Y) = (M (X ²) – M ²(X)) + (M (Y ²) – M ²(Y)) = D (X) + D (Y). Следствие 1. Дисперсия суммы нескольких взаимно независимых случайных величин равна сумме их дисперсий. Следствие 2. Дисперсия суммы постоянной и случайной величин равна дисперсии случайной величины. 4) Дисперсия разности двух независимых случайных величин равна сумме их дисперсий: D (X – Y) = D (X) + D (Y). (7.11) Доказательство. D (X – Y) = D (X) + D (- Y) = D (X) + (-1)² D (Y) = D (X) + D (X). Дисперсия дает среднее значение квадрата отклонения случайной величины от среднего; для оценки самого отклонения служит величина, называемая средним квадратическим отклонением. Определение 7.6. Средним квадратическим отклонением σ случайной величины Х называется квадратный корень из дисперсии:
Пример. В предыдущем примере средние квадратические отклонения Х и Y равны соответственно
Характеристические функции. Для доказательства центральной предельной теоремы используется метод характеристичес-ких функций.
Определение 15.1. Характеристической функциейслучайной величины Х называется функция g(t) = M (eitX) (15.1)
Таким образом, g (t) представляет собой математическое ожидание некоторой комплексной случайной величины U = eitX, связанной с величиной Х. В частности, если Х – дискретная случайная величина, заданная рядом распределения, то . (15.2) Для непрерывной случайной величины с плотностью распределения f(x) (15.3) Пример 1. Пусть Х – число выпадений 6 очков при одном броске игральной кости. Тогда по формуле (15.2) g(t) =
Пример 2. Найдем характеристическую функцию для нормированной непрерывной случайной величины, распределенной по нормальному закону. По формуле (15.3) (использовалась формула и то, что i² = -1).
Способы построения оценок. Метод моментов. Метод моментов основан на том, что начальные и центральные эмпирические моменты являются состоятельными оценками соответственно начальных и центральных теоретических моментов, поэтому можно приравнять теоретические моменты соответствующим эмпирическим моментам того же порядка. Если задан вид плотности распределения f(x, Θ), определяемой одним неизвестным параметром Θ, то для оценки этого параметра достаточно иметь одно уравнение. Например, можно приравнять начальные моменты первого порядка: , получив тем самым уравнение для определения Θ. Его решение Θ* будет точечной оценкой параметра, которая является функцией от выборочного среднего и, следовательно, и от вариант выборки: Θ = ψ (х1, х2, …, хп). Если известный вид плотности распределения f(x, Θ1, Θ2) определяется двумя неизвестными параметрами Θ1 и Θ2, то требуется составить два уравнения, например ν1 = М1, μ2 = т2. Отсюда - система двух уравнений с двумя неизвестными Θ1 и Θ2. Ее решениями будут точечные оценки Θ1* и Θ2* - функции вариант выборки: Θ1 = ψ1 (х1, х2, …, хп), Θ2 = ψ2(х1, х2, …, хп).
Метод наименьших квадратов. Если требуется оценить зависимость величин у и х, причем известен вид связывающей их функции, но неизвестны значения входящих в нее коэффициентов, их величины можно оценить по имеющейся выборке с помощью метода наименьших квадратов. Для этого функция у = φ (х) выбирается так, чтобы сумма квадратов отклонений наблюдаемых значений у1, у2,…, уп от φ(хi) была минимальной:
При этом требуется найти стационарную точку функции φ(x; a, b, c…), то есть решить систему:
(решение, конечно, возможно только в случае, когда известен конкретный вид функции φ). Рассмотрим в качестве примера подбор параметров линейной функции методом наименьших квадратов. Для того, чтобы оценить параметры а и b в функции y = ax + b, найдем Тогда. Отсюда. Разделив оба полученных уравнения на п и вспомнив определения эмпирических моментов, можно получить выражения для а и b в виде: . Следовательно, связь между х и у можно задать в виде:
Мода и медиана. Такая характеристика случайной величины, как математическое ожидание, называется иногда характеристикой положения, так как она дает представление о положении случайной величии-ны на числовой оси. Другими характеристиками положения являются мода и медиана. Определение 9.3. Модой М дискретной случайной величины называется ее наиболее вероятное значение, модой М непрерывной случайной величины – значение, в котором плотность вероятности максимальна. Пример 1. Если ряд распределения дискретной случайной величины Х имеет вид:
то М = 2. Пример 2. Для непрерывной случайной величины, заданной плотностью распределения, модой является абсцисса точки максимума: М = 0. Замечание 1. Если кривая распределения имеет больше одного максимума, распределение называется полимодальным, если эта кривая не имеет максимума, но имеет минимум – анти-модальным. Замечание 2. В общем случае мода и математическое ожидание не совпадают. Но, если распре-деление является симметричным и модальным (то есть кривая распределения симметрична от-носительно прямой х = М) и имеет математическое ожидание, оно совпадает с модой. Определение 9.4. Медианой Ме непрерывной случайной величины называют такое ее значение, для которого p (X < Me) = p (X > Me). (9.3) Графически прямая х = Ме делит площадь фигуры, ограниченной кривой распределения, на две равные части. Замечание. Для симметричного модального распределения медиана совпадает с математичес-ким ожиданием и модой. Определение 9.5. Для случайной величины Х с функцией распределения F (X) квантилью порядка р (0 < p < 1) называется число Кр такое, что F (Kp) ≤ p, F (Kp + 0) ≥ p. В частности, если F (X) строго монотонна, Кр: F (Kp) = p. Асимметрия и эксцесс. Если распределение не является симметричным, можно оценить асимметрию кривой распреде-ления с помощью центрального момента 3-го порядка. Действительно, для симметричного распределения все нечетные центральные моменты равны 0 (как интегралы от нечетных функ-ций в симметричных пределах), поэтому выбран нечетный момент наименьшего порядка, не тождественно равный 0. Чтобы получить безразмерную характеристику, его делят на σ3 (так как μ3 имеет размерность куба случайной величины). Определение 9.6. Коэффициентом асимметрии случайной величины называется . (9.4)
Рис.1. Рис.2. В частности, для кривой, изображенной на рис.1, Sk > 0, а на рис.2 - Sk < 0. Для оценки поведения кривой распределения вблизи точки максимума (для определения того, насколько «крутой» будет его вершина) применяется центральный момент 4-го порядка. Определение 9.7. Эксцессом случайной величины называется величина (9.5) Замечание. Можно показать, что для нормального распределения, и, соответственно, Ех = 0. Для кривых с более острой вершиной Ех > 0, в случае более плоской вершины Ех < 0.
Числовые характеристики двумерных случайных величин. Такие характеристики, как начальные и центральные моменты, можно ввести и для системы двух случайных величин. Определение 9.8. Начальным моментом порядка k, s двумерной случайной величины (Х, Y) называется математическое ожидание произведения Xk на Ys: α k,s = M (XkYs). (9.6) Для дискретных случайных величин для непрерывных случайных величин Определение 9.9. Центральным моментом порядка k, s двумерной случайной величины (Х, Y) называется математическое ожидание произведения (X – M (X)) k на (Y – M (Y)) s: μ k,s = M ((X – M (X)) k (Y – M (Y)) s). (9.7) Для дискретных случайных величин для непрерывных случайных величин При этом М (Х) = α1,0, M (Y) = α0,1, D (X) = μ2,0, D (Y) = μ0,2.
Корреляционный момент и коэффициент корреляции. Определение 9.10. Корреляционным моментом системы двух случайных величин называется второй смешанный центральный момент: Kxy = μ1,1 = M ((X – M (X))(Y – M (Y))). (9.8) Для дискретных случайных величин для непрерывных случайных величин Безразмерной характеристикой коррелированности двух случайных величин является коэффициент корреляции . (9.9) Корреляционный момент описывает связь между составляющими двумерной случайной вели-чины. Действительно, убедимся, что для независимых Х и Y Kxy = 0. В этом случае f (x,y) = =f 1(x) f 2(y), тогда
Итак, две независимые случайные величины являются и некоррелированными. Однако понятия коррелированности и зависимости не эквивалентны, а именно, величины могут быть зависимы-ми, но при этом некоррелированными. Дело в том, что коэффициент корреляции характеризует не всякую зависимость, а только линейную. В частности, если Y = aX + b, то rxy = ±1. Найдем возможные значения коэффициента корреляции. Теорема 9.1. Доказательство. Докажем сначала, что Действительно, если рассмотреть случай-ную величину и найти ее дисперсию, то получим:. Так как дисперсия всегда неотрицательна, то откуда Отсюда что и требовалось доказать.
Пример. При проведении 20 серий из 10 бросков игральной кости число выпадений шести очков оказалось равным 1,1,4,0,1,2,1,2,2,0,5,3,3,1,0,2,2,3,4,1.Составим вариационный ряд: 0,1,2,3,4,5. Статистический ряд для абсолютных и относительных частот имеет вид:
Если исследуется некоторый непрерывный признак, то вариационный ряд может состоять из очень большого количества чисел. В этом случае удобнее использовать группированную выборку. Для ее получения интервал, в котором заключены все наблюдаемые значения признака, разбивают на несколько равных частичных интервалов длиной h, а затем находят для каждого частичного интервала ni – сумму частот вариант, попавших в i -й интервал. Составленная по этим результатам таблица называется группированным статистическим рядом:
Примеры построения гистограмм.
По результатам тестирования по математике учащихся 7-го класса получены данные о доступности заданий теста (отношение числа учащихся, правильно выполнивших задания, к числу тестировавшихся учащихся), предствленные ниже, в таблице.
Решение. Откладываем на оси абсцисс 7 отрезков длиной 10. На них, как на основаниях, строим прямоугольники, высоты которых соответственно равны 1, 1, 5, 7, 7, 3, 1. Полученная ступенчатая фигура и является искомой гистограммой.
Данные, приведенные в предыдущем примере представим более подробно (см. таблицу ниже.). Построить гистограмму.
Решение. Далее на рисунке построена гистограмма по этим данным. Получено изображение более подробной информации о распределении данных. Случайные величины Случайной называют величину, которая в результате испытания примет одно и только одно возможное значение, наперед неизвестное и зависящее от случайных причин, которые заранее не могут быть учтены. Пример I. Число родившихся мальчиков среди ста новорожденных есть случайная величина, которая имеет ледующие возможные значения: 0, 1, 2 100. Пример 2. Расстояние, которое пролетит снаряд прн нистреле из орудия, есть случайная величина. Действительно, расстояние зависит не только от установки прицела, но и от многих других причин (силы и направления ветра, температуры и т. д.), которые не могут быть полностью учтены. Возможные значения этой величины принадлежат некоторому промежутку (а, Ь). Мы будем далее обозначать случайные величины прописнымими буквами X, Y, Z, а их возможные значения соответствующими строчными буквами х, у, z. Например, если случайная величина X имеет три возможных значения, то они будут обозначены так: x1, х2, х3. Оглавление Вопрос 1. Метод моментов. 2 Вопрос 2. Теорема умножения вероятностей. 3 Вопрос 3. Понятие начального и центрального моментов. 5 Вопрос 4. Понятие генеральной и выборочной совокупности. 6 Вопрос 5. Оценка числовых характеристик. 9 Вопрос 6. Показательный закон распределения и его свойства. 14 Вопрос 7. Формула Байеса (теорема гипотез) 15 Вопрос 8. Математическое ожидание и его свойства. 16 Вопрос 9. Условный закон распределения двумерной случайной величины.. 19 Вопрос 10. Теорема умножения независимых событий. 21 Вопрос 11. Неравенство Чебышева. 22 Вопрос 12. Классификация событий. 24 Вопрос 13. Нормальный закон распределения и его свойства. 25 Вопрос 14. Равномерный закон и его свойства. 27 Свойства плотности распределения. 27 Равномерный закон распределения. 28 Вопрос 15. Центральная предельная теорема. 30 Характеристические функции. 30 Сво
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Последнее изменение этой страницы: 2016-04-25; просмотров: 343; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.16.49.213 (0.017 с.) |

 ,
, - система двух уравнений с двумя неизвестными Θ1 и Θ2. Ее решениями будут точечные оценки Θ1* и Θ2* - функции вариант выборки:
- система двух уравнений с двумя неизвестными Θ1 и Θ2. Ее решениями будут точечные оценки Θ1* и Θ2* - функции вариант выборки: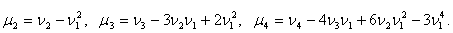
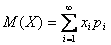 , если полученный ряд сходится абсолютно.
, если полученный ряд сходится абсолютно.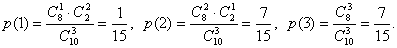 Тогда
Тогда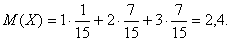
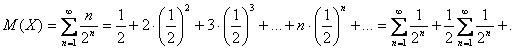 ..+
..+ (при вычислении дважды использовалась формула суммы бесконечно убывающей геометрической прогрессии:
(при вычислении дважды использовалась формула суммы бесконечно убывающей геометрической прогрессии: 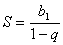 , откуда
, откуда 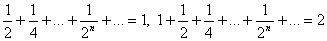 ).
).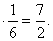 Тому же числу равно математическое ожидание числа очков, выпавших на любой кости. Следовательно, по свойству 4 М (Х)=
Тому же числу равно математическое ожидание числа очков, выпавших на любой кости. Следовательно, по свойству 4 М (Х)= 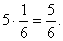

 . (7.12)
. (7.12)





