
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теорема Коши. Физический смысл.Содержание книги Похожие статьи вашей тематики
Поиск на нашем сайте
Теорема: (Коши о среднем) Пусть функции f(x) и g(x) непрерывны на отрезке [ a,b ] и имеют производные на интервале (a,b), одновременно не обращающиеся в ноль. При этом g(b)-g(a)¹0 ( что следует из условия g΄(x)¹0). Тогда на интервале (a,b) найдется точка ζ, для которой выполняется неравенство:
Доказательство: Вводим функцию H(x)=(f(b)-f(a))·g(x)-(g(b)-g(a))·f(x). Очевидно, что она непрерывна на [ a,b ] и имеет производную на (a,b), т.к. f(b)-f(a) и g(b)-g(a) постоянны. Кроме того, H(a)=H(b), поэтому по теореме Ролля найдется такая точка ζ из (a,b), что H΄(ζ)=0. H΄(ζ)=(f(b)-f(a))·g΄(ζ)-(g(b)-g(a))·f΄(ζ)Þ (f(b)-f(a))·g΄(ζ)=(g(b)-g(a))·f΄(ζ) Теорема доказана. Физический смысл: Если f΄(x) и g΄(x) – скорости, то отношение перемещений равно отношению скоростей в какой-то момент времени.
Билет 14 Теорема о среднем Лагранжа. Теорема: Пусть функция
причем Доказательство: В теореме Коши, возьмем Из теоремы Коши: Физический смысл: Найдется момент времени когда
Теорема Лагранжа утверждает, что если кривая есть график непрерывной на Равенство (1) называется формулой (Лагранжа) конечных приращений. Промежуточное значение
Она верна, очевидно, не только для Билет 15 Достаточное условие невозрастания (неубывания) функции на отрезке. Условие постоянства функции на отрезке.
Определение: Функция Определение: Функция Определение: Функция Определение: Функция Пример: Если Теорема 1: (необходимое условие возрастания (неубывания) функции в точке Если функция Доказательство:
Теорема доказана. Пример: Теорема 1’: (необходимое условие убывания (невозрастания) функции в точке Если функция Доказательство – аналогично теореме 1. Теорема 2: (достаточное условие возрастания) Если функция Доказательство:
Теорема доказана. Замечание: Если в точке Билет 16 Достаточные условия экстремума. Теорема 1: (первое достаточное условие существования экстремума) Если f(x) дифференцируема в Доказательство: Т.к f(x) с одной стороны возрастает, с другой убывает, т.е.
Теорема доказана. Теорема 2: (второе достаточное условие существования экстремума) Если в Доказательство: f’( f’(x) в точке f’(x) в точке 1) f’’(
при x<
2) Аналогично для f’’(
Билет 17 Формула Тейлора для многочленов. Рассмотрим произвольный многочлен степени n: (1) Пусть a – любое фиксированное число, тогда, полагая (2) Это выражение называют разложение многочлена Подставим в выражение (2) (3) Найдем последовательные производные
Таким образом, многочлен
или
Последняя формула называется формулой Тейлора для многочлена
Билет 18
|
||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 572; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.137.186.26 (0.006 с.) |

 , a<ζ<b.
, a<ζ<b. , т.к. по условию g(b)-g(a)¹0 и g΄(x)¹0 на (a,b).
, т.к. по условию g(b)-g(a)¹0 и g΄(x)¹0 на (a,b).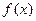 непрерывна на отрезке
непрерывна на отрезке  и имеет производную на интервале
и имеет производную на интервале  . Тогда существует на интервале
. Тогда существует на интервале  , для которой выполняется равенство
, для которой выполняется равенство (1),
(1), .
. . Тогда
. Тогда  ,
,  ,
,  .
.
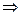
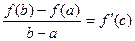 теорема доказана.
теорема доказана. (средняя скорость равна мгновенной)
(средняя скорость равна мгновенной) Геометрический смысл:
Геометрический смысл: такая, что касательная к кривой в этой точке параллельна хорде, стягивающей концы кривой
такая, что касательная к кривой в этой точке параллельна хорде, стягивающей концы кривой  и
и  .
. , где
, где  есть некоторое число, удовлетворяющее неравенствам
есть некоторое число, удовлетворяющее неравенствам  . Тогда формула Лагранжа примет вид
. Тогда формула Лагранжа примет вид

 , но и для
, но и для 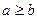 .
.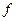 называется строго возрастающей на отрезке [a,b], если для любых точек
называется строго возрастающей на отрезке [a,b], если для любых точек  ,
,  из [a,b], удовлетворяющих неравенству
из [a,b], удовлетворяющих неравенству 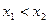 , имеет место неравенство
, имеет место неравенство 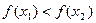 .
.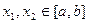 и
и  .
. .
.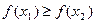 .
.
 и на
и на 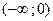 , то нельзя говорить, что
, то нельзя говорить, что  .
. )
)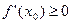 .
.
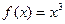 возрастает в 0 и
возрастает в 0 и 
 .
. , то
, то 

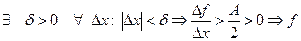 возрастает.
возрастает. , f’ имеет разные знаки слева и справа от Xo => Xo – точка экстремума.
, f’ имеет разные знаки слева и справа от Xo => Xo – точка экстремума. - max
- max - min
- min f(
f( при x<
при x< 
 , получим
, получим
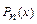 по степеням
по степеням  . Здесь
. Здесь 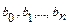 – числа, зависящие от
– числа, зависящие от 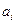 и
и  , – коэффициенты разложения
, – коэффициенты разложения 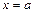 , получим
, получим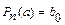



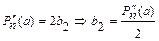



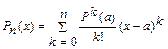
 .
.


