
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Необходимое и достаточное условие дифференцируемости.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Пусть функция Тогда и приращение в точке может быть записано в виде:
ведь выражение Определение. Функция где А не зависит от Теорема 1: Для того, чтобы функция Доказательство: Достаточность условия доказана выше: из существования конечной производной Необходимость условия. Пусть функция Предел правой части при Это означает, что существует производная Билет 9 Производные высших порядков. Формула Лейбница.
Пусть функция y=f(x) дифференцируема в точке Xo, то есть существует ее производная в этой точке f ’ (Xo). Пусть f - дифференцируема в некоторой окрестности U(Xo). f’(x) определена на U(Xo) и если дифференцируема в точке Xo, то (f’(Xo))’=f’’(Xo). Вообще Теорема: (Формула Лейбница) Пусть функции U и V n раз дифференцируемы, т.е. существуют
Доказательство: Метод математической индукции: Пусть при n=m – верно, т.е.
Надо доказать, что
Доказательство:
Теорема доказана. Билет 10 Дифференциалы высших порядков. Инвариантность формы первого дифференциала. Неинвариантность формы дифференциалов второго и высших порядков. f(x) дифференцируема, тогда
__________________________
1) 2) Пусть при n = m 3)
Инвариантность/Неинвариантность. 1) y(x), x – независимая переменная,
2) y(x), x – независимая переменная,
Билет 11 Возрастание (убывание) функции в точке. Необходимое и достаточное условие. Теорема Ферма. Определение 1:. f(x) – возрастает (не убывает) в точке
Определение 1’. f(x) – возрастает (не убывает) в точке
Определение 1’’. f(x) – возрастает (не убывает) в точке
Определение 2. f(x) – убывает (не возрастает) в точке
Определение 2’. f(x) – убывает (не возрастает) в точке
Определение 2’’. f(x) – убывает (не возрастает) в точке
Теорема 1: (Необходимое условие возрастания (неубывания) функции в точке Если f возрастает (не убывает) в точке Доказательство: Т.к. функция возрастает (не убывает), то, по определению 1’’,
Теорема 1’ (Необходимое условие убывания (невозрастания) функции в точке Если f убывает (не возрастает) в точке Доказательство: Т.к. функция убывает (не возрастает), то, по определению 2’’,
Теорема 2: (Достаточное условие возрастания) Если f(x) дифференцируема в точке Доказательство: По теореме о сохранении знака:
Теорема доказана. Замечание: если Теорема 2’: (Достаточное условие убывания) Если f(x) дифференцируема в точке Доказательство: По теореме о сохранении знака:
Теорема доказана. Замечание: если Теорема Ферма: (Необходимое условие существования экстремума) Если f(x) дифференцируема в точке Доказательство: Пусть
Аналогично невозможен случай Теорема доказана. Билет 12 Теорема Ролля. Теорема: Если функция Доказательство: Так как функция f непрерывна на [a,b], то существует точка x1, в которой f достигает максимума и точка x2, в которой f достигает минимума. Рассмотрим 2 случая:
И тогда
Контрпример 1
Уберем непрерывность в точке b: теорема потеряет силу.
Контрпример 2 Уберем дифференцируемость в одной из точек: теорема потеряет силу.
Теорема Ролля имеет простой геометрический смысл: если выполнены все условия теоремы, то на графике функции!
Физический смысл: при прямолинейном движении если перемещение тела = 0, то существует момент времени, в который скорость тела = 0.
Билет 13
|
||||||
|
Последнее изменение этой страницы: 2016-08-16; просмотров: 3496; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.144.37.178 (0.012 с.) |

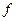 имеет производную в точке
имеет производную в точке  (конечную):
(конечную): 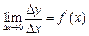 .
. для достаточно малых
для достаточно малых  можно записать в виде суммы
можно записать в виде суммы  и некоторой функции, которую мы обозначим через
и некоторой функции, которую мы обозначим через  , которая стремится к нулю вместе с
, которая стремится к нулю вместе с 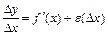
 ,
, 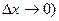
 или
или 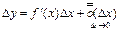 (1),
(1),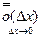 понимается как функция от
понимается как функция от 
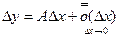 (2),
(2), в виде (1), где можно положить
в виде (1), где можно положить  .
. , получаем
, получаем  .
.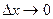 существует и равен А:
существует и равен А:  .
.
 и
и  . Значит (U*V) – тоже n раз дифференцируема, при этом
. Значит (U*V) – тоже n раз дифференцируема, при этом
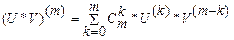 (*)
(*)
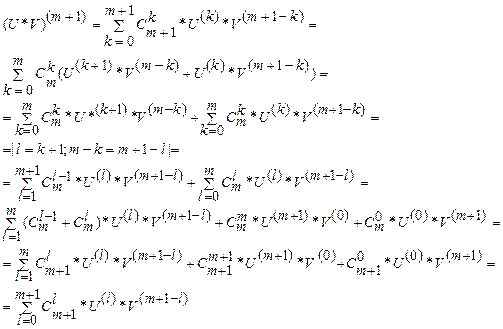

 . Далее, пусть f – n раз дифференцируема,
. Далее, пусть f – n раз дифференцируема, 
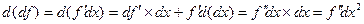
 . Докажем, что
. Докажем, что 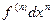
 ,
, 
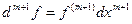
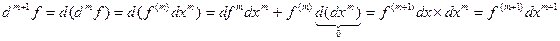
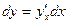 , пусть x = x(t)
, пусть x = x(t)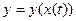

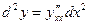 ,
,  ,
, 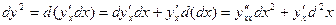 , здесь
, здесь  ,
,  .
.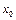 , если
, если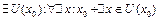
 .
.

 .
.
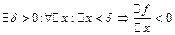
 .
. , а значит и
, а значит и  . Теорема доказана.
. Теорема доказана. .
.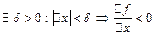 , а значит и
, а значит и 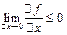 , теорема доказана.
, теорема доказана. , то f(x) возрастает в точке
, то f(x) возрастает в точке 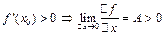 , значит
, значит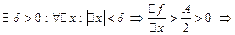 f возрастает.
f возрастает. , то f(x) убывает в точке
, то f(x) убывает в точке 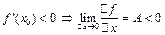 , значит
, значит f(x) убывает.
f(x) убывает. .
. f(x) возрастает в точке
f(x) возрастает в точке 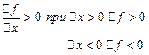 , т.е.
, т.е.  непрерывна на
непрерывна на 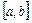 , дифференцируема на
, дифференцируема на 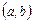 и
и  , то существует точка
, то существует точка 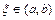 , такая, что
, такая, что  .
.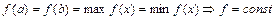
 производная
производная 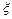 - та из них, которая
- та из них, которая  , тогда в точке
, тогда в точке  , так как по условию
, так как по условию 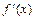 существует
существует 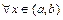 . Поэтому по теореме Ферма
. Поэтому по теореме Ферма 

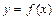 существует точка
существует точка 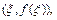 касательная в которой параллельна оси x.
касательная в которой параллельна оси x.



