
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Производная. Определение, непрерывность функции, имеющей производную.Содержание книги
Поиск на нашем сайте
Билет 1 Производная. Определение, непрерывность функции, имеющей производную. Определение: Производной от функции
Т.е., если
Теорема: (необходимое условие существования производной) Если функция Доказательство:
При Следовательно Теорема доказана.
Замечание: обратное утверждение неверно, если функция Контрпример: Утверждение: если функция имеет в точке правую и левую производную, то она непрерывна и справа и слева. Контрпример:
Билет 2 Геометрический смысл производной.
Теорема 1: График функции имеет невертикальную касательную тогда и только тогда, когда существует конечное значение производной этой функции в данной точке.
Доказательство: Пусть существует значение f’(
при Секущая стремится к касательной.
Пусть существует невертикальная касательная => существует Секущая стремится к касательной.
Теорема доказана. Билет 3 Арифметические свойства производной. Пусть f = f(x) и g = g(x) – функции, имеющие конечные производные в точке x0, тогда справедливы равенства: 1. 2. 2.1. 3. ----------------------------------------------------------------------------------------------------------------------------- 1.
2.
Заметим, что функция f, как имеющая производную, непрерывна, и потому при
3.
Билет 4 Производная обратной функции. Определение: Пусть на интервале (a,b) задана непрерывная строго монотонная, т.е. строго возрастающая или строго убывающая, функция Зафиксируем Наоборот, Вследствие непрерывности прямой и обратной функций для указанных Пусть теперь функция Так как из того, что
Этим доказано, что если Может случится, что в точке Если же Пример 1.
Если логарифм натуральный, то
Функция ln x как действительная функция определена только для положительных значений х. Пример 2.
где Пример 3.
Пример 4. Функция
Пример 5.
Пример 6.
Билет 5 Производная сложной функции.
Теорема: Пусть функция Доказательство:
Рассмотрим ∆H:
Билет 6 Производные элементарных функций. 1.
2.
3.
4.
Замечание: если функция имеет конечную производную в точке, то она непрерывна в этой точке (было доказано в Билете 1), но она может быть разрывной в любой другой точке, кроме этой. Пример:
Билет 7 Билет 8 Билет 9 Производные высших порядков. Формула Лейбница.
Пусть функция y=f(x) дифференцируема в точке Xo, то есть существует ее производная в этой точке f ’ (Xo). Пусть f - дифференцируема в некоторой окрестности U(Xo). f’(x) определена на U(Xo) и если дифференцируема в точке Xo, то (f’(Xo))’=f’’(Xo). Вообще Теорема: (Формула Лейбница) Пусть функции U и V n раз дифференцируемы, т.е. существуют
Доказательство: Метод математической индукции: Пусть при n=m – верно, т.е.
Надо доказать, что
Доказательство:
Теорема доказана. Билет 10 Дифференциалы высших порядков. Инвариантность формы первого дифференциала. Неинвариантность формы дифференциалов второго и высших порядков. f(x) дифференцируема, тогда
__________________________
1) 2) Пусть при n = m 3)
Инвариантность/Неинвариантность. 1) y(x), x – независимая переменная,
2) y(x), x – независимая переменная,
Билет 11 Билет 12 Теорема Ролля. Теорема: Если функция Доказательство: Так как функция f непрерывна на [a,b], то существует точка x1, в которой f достигает максимума и точка x2, в которой f достигает минимума. Рассмотрим 2 случая:
И тогда
Контрпример 1 Уберем непрерывность в точке b: теорема потеряет силу.
Контрпример 2 Уберем дифференцируемость в одной из точек: теорема потеряет силу.
Теорема Ролля имеет простой геометрический смысл: если выполнены все условия теоремы, то на графике функции!
Физический смысл: при прямолинейном движении если перемещение тела = 0, то существует момент времени, в который скорость тела = 0.
Билет 13 Билет 14 Теорема о среднем Лагранжа. Теорема: Пусть функция
причем Доказательство: В теореме Коши, возьмем Из теоремы Коши: Физический смысл: Найдется момент времени когда
Теорема Лагранжа утверждает, что если кривая есть график непрерывной на Равенство (1) называется формулой (Лагранжа) конечных приращений. Промежуточное значение
Она верна, очевидно, не только для Билет 15 Билет 16 Билет 17 Билет 18 Билет 19 Билет 20 Билет 22 Билет 23 A – конечное. Доопределим функции: f(a)=0 и g(а) = 0; f(x) и g(x) непрерывны на [a;x]
f(a)=g(a)=0 =>
2) Пусть Введем функции
Теорема доказана. Замечание: обратное неверно. Пример: Билет 24 Правило Лопиталя. Случай Теорема: Пусть функции f и g определены и дифференцируемы в некоторой окрестности точки a и
Доказательство: Возьмем произвольную последовательность
Тогда
Тогда можно найти такой номер, для которого будут выполняться оба неравенства:
Используя термины
Найдем теперь предел отношения
Мы получили еще не совсем теорему о сходимости последовательности через подпоследовательности, (ее формулировка: если Теперь возьмем произвольную последовательность Теперь мы взяли произвольную последовательность, поэтому Причем важно, чтобы предел отношения производных существовал. Теорема доказана.
Билет 25 Раскрытие неопределенностей вида
Кроме рассмотренных неопределенностей 1) Неопределенность Ясно, что 2) Неопределенности вида Согласно определению этой функции 3) Неопределенность Легко видеть, что Билет 26 Билет 27 Первообрáзная. Неопределенный интеграл. Свойства. Определение 1: Функция F называется первообразной функции f на интервале (a,b), если функция f непрерывна на интервале (a,b), и для всех x из этого интервала выполняется равенство: F΄(x)=f(x). Замечание: Вместо (a,b) можно рассматривать [a,b], (a,b] и [a,b), но нужно будет говорить про односторонние производные: Пример
на промежутке (-∞,0) и на (0,+∞).
Теорема: (О множестве всех первообразных). Пусть F(x) является первообразной функции f(x) на на промежутке I, тогда функции вида F(x)+C и только они являются первообразными функции f(x), где C – произвольная константа. Доказательство: Пусть функция F(x) – первообразная функции f(x), тогда F΄(x)=f(x) и (F(x)+C)΄=f(x). Пусть функции F и G – первообразные функции f(x) на промежутке I (нужно доказать, что они отличаются на константу). Тогда (F-G)΄=0 Теорема доказана. Определение 2: Множество всех первообразных функции f(x) на промежутке I называется неопределенным интегралом и обозначается Пример:
Свойства первообразных и неопределенного интеграла. 1. Пусть функция f(x) имеет первообразную F(x) на промежутке I и функция g(x) имеет первообразную G(x) на промежутке I, тогда функция f(x)±g(x) будет иметь первообразную F(x)±G(x) на промежутке I. Для интегралов: Замечание: Обратное неверно! Из существования интеграла Первообразной функции k·f(x) является функция k·F(x). Для интегралов: 2. Первообразной производной функции f΄(x) является сама функция f(x). Для интегралов: 3. Билет 28 Билет 29 Билет 30 Билет 31 Билет 32 Интегрирование выражений вида Докажем, что любой такой интеграл – берущийся в элементарных функциях. Пусть Тогда получим, что x=φ(t), dx=φ΄(t)dt, где φ(t) и φ΄(t)dt – рациональные выражения, поэтому: Билет 33 Первая подстановка Эйлера (Леонарда)
Пусть многочлен Пусть Рассмотрим подстановку
Билет 34 Вторая подстановка Эйлера для интегралов вида Корни трехчлена ax2+bx+c комплéксные. Тогда надо считать, что a>0, иначе трехчлен был бы отрицателен для всех x. Делаем подстановку
Где x, y и dx – некоторые рациональные функции от t. В конечном счете получаем:
Билет 35 Билет 36 Билет 37 Определенный интеграл Римана. Эквивалентные определения. Условие Коши. Пусть задана функция f(x) на отрезке
Это интегральная сумма, соответствующая разбиению R и выбору точек Если существует предел при
Определение по Коши:
По Гейне:
Критерий Коши:
Билет 38 Билет 39 Суммы Дарбу. Их Свойства. Определение: Пусть R: Тогда можем составить выражения:
Пусть R: Тогда можем составить выражения:
Свойства сумм Дарбу: 1) 2) Рассмотрим два разбиения в случае, когда одно разбиение является продолжением другого. Т.е.
Заметим, что если
3)
=>
Билет 40 Билет 41 Билет 42 Теорема 2 Функция непрерывная на отрезке, равномерно непрерывна на нем ( Доказательство: Допустим что теорема неверна. Построим отрицание к определению 2.
Необходимость условия: Если Пример | ||
|
| Поделиться: |

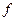 в точке
в точке  называется предел, к которому стремится отношение ее приращения
называется предел, к которому стремится отношение ее приращения  в этой точке к соответствующему приращению
в этой точке к соответствующему приращению  аргумента, когда последнее стремится к нулю:
аргумента, когда последнее стремится к нулю:
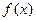 определена в
определена в  , то
, то
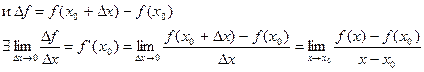
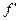 в точке
в точке  , то
, то 
 ,
,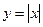



 )-конечное, тогда
)-конечное, тогда



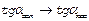
 =>
=>  ч.т.д.
ч.т.д. - конечный.
- конечный. =>
=> 


 где k – константа
где k – константа





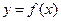 . Пусть образ (a,b) есть интервал (A,B). тогда обратная к
. Пусть образ (a,b) есть интервал (A,B). тогда обратная к  есть однозначная непрерывная и строго монотонная на (A,B) функция.
есть однозначная непрерывная и строго монотонная на (A,B) функция.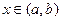 и дадим ему приращение
и дадим ему приращение  Тогда
Тогда 

 имеет место утверждение: из
имеет место утверждение: из  следует
следует 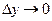 , и обратно.
, и обратно.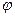 в точке у имеет неравную нулю производную
в точке у имеет неравную нулю производную  . Покажем, что в таком случае функция
. Покажем, что в таком случае функция 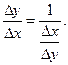

 , то функция
, то функция  В этом случае, очевидно, функция
В этом случае, очевидно, функция  .
. , то для строго возрастающей функции при этом
, то для строго возрастающей функции при этом  , а для строго убывающей
, а для строго убывающей  . В первом случае
. В первом случае  , а во втором
, а во втором 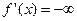 .
.
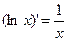 .
.


 строго возрастает на отрезке [-1,1] и отображает этот отрезок на
строго возрастает на отрезке [-1,1] и отображает этот отрезок на  Обратная к ней функция
Обратная к ней функция  имеет производную
имеет производную  положительную на интервале
положительную на интервале  . Поэтому
. Поэтому


 , и функция
, и функция  такая, что
такая, что  ,
,  . Тогда функция
. Тогда функция  и
и  .
.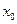 , тогда:
, тогда: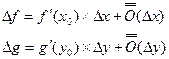

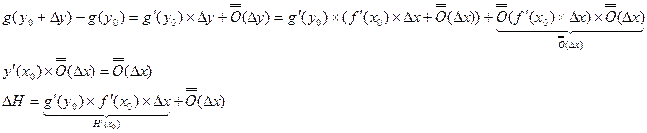
 ;
; 









 (т.к. функция непрерывна)
(т.к. функция непрерывна)
 , т.к.
, т.к.








 - не выполняется критерий Коши и в каждой точке
- не выполняется критерий Коши и в каждой точке 
 и
и  . Значит (U*V) – тоже n раз дифференцируема, при этом
. Значит (U*V) – тоже n раз дифференцируема, при этом
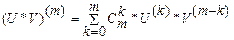 (*)
(*)
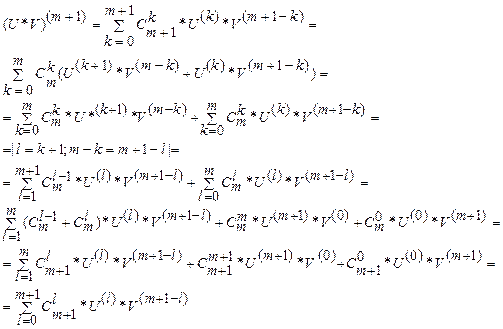

 . Далее, пусть f – n раз дифференцируема,
. Далее, пусть f – n раз дифференцируема, 
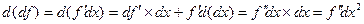
 . Докажем, что
. Докажем, что 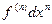
 ,
, 
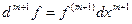
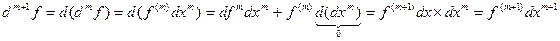
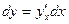 , пусть x = x(t)
, пусть x = x(t)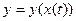

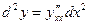 ,
,  ,
, 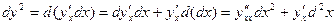 , здесь
, здесь  ,
,  .
. непрерывна на
непрерывна на 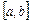 , дифференцируема на
, дифференцируема на 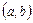 и
и  , то существует точка
, то существует точка 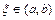 , такая, что
, такая, что  .
.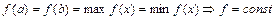
 производная
производная 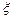 - та из них, которая
- та из них, которая  , тогда в точке
, тогда в точке  , так как по условию
, так как по условию 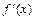 существует
существует 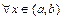 . Поэтому по теореме Ферма
. Поэтому по теореме Ферма 

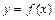 существует точка
существует точка 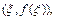 касательная в которой параллельна оси x.
касательная в которой параллельна оси x.
 и имеет производную на интервале
и имеет производную на интервале  . Тогда существует на интервале
. Тогда существует на интервале  , для которой выполняется равенство
, для которой выполняется равенство (1),
(1), .
. . Тогда
. Тогда  ,
,  ,
,  .
.
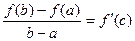 теорема доказана.
теорема доказана. (средняя скорость равна мгновенной)
(средняя скорость равна мгновенной) Геометрический смысл:
Геометрический смысл: такая, что касательная к кривой в этой точке параллельна хорде, стягивающей концы кривой
такая, что касательная к кривой в этой точке параллельна хорде, стягивающей концы кривой  и
и  .
. , где
, где  есть некоторое число, удовлетворяющее неравенствам
есть некоторое число, удовлетворяющее неравенствам  . Тогда формула Лагранжа примет вид
. Тогда формула Лагранжа примет вид

 , но и для
, но и для 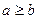 .
.
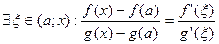 при
при 
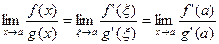
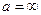


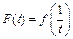 и
и 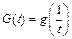
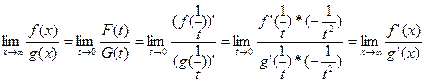
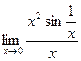
 .
.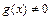 и
и 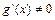 в некоторой выколотой окрестности точки a, тогда, если
в некоторой выколотой окрестности точки a, тогда, если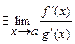 , то
, то 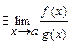 и
и 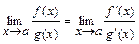
 ,
,  ,
, 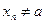 , тогда по определению предела по Гейне
, тогда по определению предела по Гейне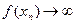 и
и 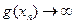
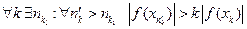 - для f(x) определение предела вида |f(x)|>C, где C =
- для f(x) определение предела вида |f(x)|>C, где C = 
 - аналогично для g(x)
- аналогично для g(x)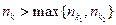
 ,
, 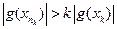
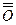 можно записать:
можно записать: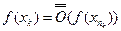 ,
, 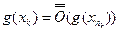 Пояснение:
Пояснение: 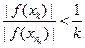 , а т.к.
, а т.к. 
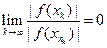
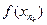 к
к 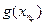 :
: [ можно добавить или отнять
[ можно добавить или отнять 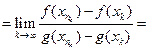 [ воспользуемся теоремой Коши:
[ воспользуемся теоремой Коши: 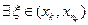 или
или 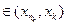 - смотря, что больше]
- смотря, что больше]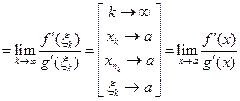 - по определению предела по Гейне.
- по определению предела по Гейне.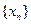 такова, что из любой её подпоследовательности
такова, что из любой её подпоследовательности 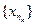 можно извлечь в свою очередь подпоследовательность
можно извлечь в свою очередь подпоследовательность  , сходящуюся к конечному или бесконечному А, то предел
, сходящуюся к конечному или бесконечному А, то предел  , т. е.
, т. е. 
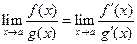
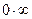 ,
, 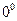 ,
,  ,
,  ,
, 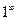 .
.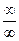 и
и 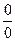 , встречаются неопределенности вида
, встречаются неопределенности вида 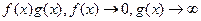 при
при 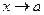 ).
).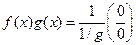 или
или  .
.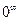 ,
, 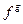 сводятся к неопределенности
сводятся к неопределенности 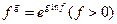 .
. 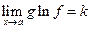 , то
, то 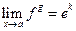 .
.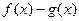 ,
, 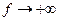 ,
, 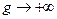 при
при 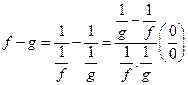 .
. =f(a), и
=f(a), и  =f(b).
=f(b).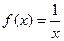 .
.
 . При этом если функция F(x) – первообразная функции f(x), то
. При этом если функция F(x) – первообразная функции f(x), то  .
. .
. .
. не следует существование интегралов
не следует существование интегралов  .
. .
. .
. (по определению).
(по определению).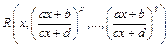 .
. , т.к.
, т.к. 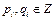 . Пусть m=НОК
. Пусть m=НОК 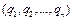 ,
, 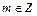 . Сделаем замену:
. Сделаем замену:  , тогда
, тогда  , причем последнее выражение - рациональное, т.к. m делится на любое
, причем последнее выражение - рациональное, т.к. m делится на любое 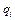 .
.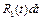 - тоже рациональное выражение
- тоже рациональное выражение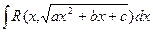
 имеет вещественные корни.
имеет вещественные корни. - корни, тогда
- корни, тогда 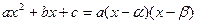 .
.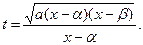
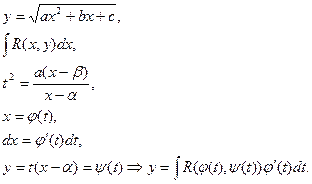
 , где
, где 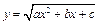 .
.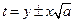 .Возводя это равенство в квадрат и заменяя
.Возводя это равенство в квадрат и заменяя 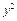 его выражением, получим:
его выражением, получим:
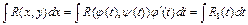 .
. . Составим разбиение R:
. Составим разбиение R:  .
.

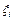 .
. интегральных сумм
интегральных сумм  , и он не зависит от R и
, и он не зависит от R и 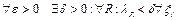

 , где
, где  - последовательность разбиений.
- последовательность разбиений.

 . Введём разбиение R этого отрезка.
. Введём разбиение R этого отрезка. ,
,  .
. - нижняя сумма Дарбу,
- нижняя сумма Дарбу,  - верхняя сумма Дарбу.
- верхняя сумма Дарбу. ,
,  .
. , для одного и того же разбиения.
, для одного и того же разбиения. - продолжение
- продолжение  , если все точки
, если все точки 
 Добавление точек не увеличивает
Добавление точек не увеличивает  и не уменьшает
и не уменьшает  . Пусть
. Пусть  ,
,  ,
, ,
, ,
,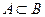 , то
, то  и
и  . Отсюда заключаем:
. Отсюда заключаем: ,
,  ,
,  ,
,  .
.
 ,
,  ,
, ,
, , т.е.
, т.е.  .
.
 - нижний интеграл (нижняя точная сумма Дарбу).
- нижний интеграл (нижняя точная сумма Дарбу).  .
. - верхний интеграл (верхняя точная сумма Дарбу).
- верхний интеграл (верхняя точная сумма Дарбу).  .
.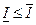 .
. ).
). . Зададим стремящуюся к нулю последовательность положительных чисел
. Зададим стремящуюся к нулю последовательность положительных чисел  , тогда
, тогда  . Так как точки последовательности
. Так как точки последовательности  принадлежат к отрезку
принадлежат к отрезку  , сходящуюся к некоторой точке
, сходящуюся к некоторой точке  . Значит, из нее можно выделить также подпоследовательность
. Значит, из нее можно выделить также подпоследовательность  . Аналогично выделим подпоследовательность
. Аналогично выделим подпоследовательность  и
и 
 . Получили противоречие – теорема доказана.
. Получили противоречие – теорема доказана. , то теорема 2 не выполняется.
, то теорема 2 не выполняется. Пусть
Пусть  при
при 


