
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Теореми Ферма і Ролля, Коші і Лагранжа.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте У курсі математичного аналізу одне з центральних місць займають так звані теореми про середнє значення, до яких належать теореми Ролля, Лагранжа і Коші. В цих теоремах йдеться про те, що коли функція та її похідна першого порядку задовольняють певним умовам, то всередині інтервалу 1. Теорема Ролля Теорема. Нехай функція 1) визначена і неперервна на відрізку 2) диференційована в інтервалі 3) на кінцях відрізка набуває однакових значень: Тоді всередині інтервалу Д о в е д е н н я. Випадок 1. Функція Тоді Випадок 2. Функція Через те, що Покажемо, що Справді, оскільки Тоді для всіх Розглянемо відношення причому Перейдемо в цих нерівностях до границі, коли Звідси випливає, що З’ясуємо геометричний зміст теореми Ролля (рис.6.9): 1) графік функції є суцільна лінія ( 2) крива, що є графіком функції, є гладкою кривою (крива називається гладкою, якщо в кожній її точці можна провести дотичну); 3) крайні точки графіка знаходяться на однаковій висоті від 2. Теорема Лагранжа Теорема. Якщо функція Д о в е д е н н я. Розглянемо функцію що задовольняє всім умовам теореми Ролля. Справді, Отже, існує точка звідси Теорему доведено. Геометрична інтерпретація теореми Лагранжа. Нехай графік функції зображено на рис. 6.10. Відношення Оскільки
Рис.6.19 Рис.6.10 Отже, рівність (6.73) можна записати в такому вигляді: або Зокрема, покладемо Вираз, який стоїть у лівій частині останньої рівності, є не що інше, як приріст Формула (6.74) виражає точне значення приросту функції в точці Наслідок 1. Якщо функція Д о в е д е н н я. Візьмемо в проміжку дві довільні точки Проте Оскільки Тепер ми можемо сформулювати такий критерій сталості диференційованої функції на заданому проміжку: для того, щоб диференційована на проміжку функція Наслідок 2. Якщо функції Д о в е д е н н я. Позначимо різницю Тоді функція Проте 3. Теорема Коші Теорема. Нехай: 1) функції
Формула Тейлора. 1. Формула Тейлора для многочлена Нехай задано многочлен де Виразимо коефіцієнти даного многочлена через значення многочлена З цією метою будемо послідовно диференціювати многочлен. Матимемо .................... Підставляючи в ці рівності .......... Тоді многочлен Може трапитися, що многочлен Формулу (6.77) називають формулою Тейлора для многочлена. 2. Формула Тейлора для довільної функції Візьмемо довільну функцію Тоді для такої функції можна побудувати многочлен Цей многочлен називається многочленом Тейлора для функції Розглянемо таку різницю: Оскільки Тоді або Формула (6.79) називається формулою Тейлора для функції Отже, формула Тейлора (6.79) відрізняється від формули Тейлора (6.77) для многочлена тим, що вона містить залишковий член Теорема. Якщо де Формула (6.79) записується тепер у вигляді і справедлива для будь-якого Формула (6.81) називається формулою Тейлора із залишковим членом виду Лагранжа. Якщо в цій формулі покласти Враховуючи вирази для диференціалів різних порядків функції 3. Формула Тейлора для функції двох змінних Нехай функція де Аналогічний вигляд має формула Тейлора для функції більшого числа змінних.
Функції багатьох змінних.
Множини точок на площині та в п – вимірному просторі. Множина точок називається зв’язною, якщо будь-які її дві точки можна сполучити ламаною лінією так, щоб усі точки цієї лінії належали цій множині.
Множина точок називається обмеженою, якщо всі її точки належать множині точок круга скінченного радіуса.
Множина точок, координати яких задовольняють нерівність
Точка називається внутрішньою для множини точок, якщо вона лежить з деяким своїм околом, і зовнішньою, якщо існує її окіл з точок, жодна з яких не належить цій множині.
Зв’язна множина., яка складається тільки з внутрішніх точок, називається відкритою областю. Позначається
Точка називається межевою для області, якщо в будь-якому її околі існують точки, що не належать області і належать їй.
Множина межевих точок називається межею області
Область, з’єднана зі своєю межею, називається замкненою областю
|
||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 871; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.011 с.) |

 знайдеться точка, в якій функція має певні властивості (про ці властивості йдеться в теоремі). Тому й самі теореми називають теоремами про середнє.
знайдеться точка, в якій функція має певні властивості (про ці властивості йдеться в теоремі). Тому й самі теореми називають теоремами про середнє. задовольняє умовам:
задовольняє умовам: :
: .
.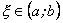 в якій
в якій 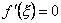 .
. .
. , тобто в кожній точці
, тобто в кожній точці  похідна дорівнює нулю, а тому за точку
похідна дорівнює нулю, а тому за точку  можна взяти будь-яку точку інтервалу і для цієї точки теорема буде справедлива.
можна взяти будь-яку точку інтервалу і для цієї точки теорема буде справедлива. , а найменше – через
, а найменше – через  . Зрозуміло, що в розглянутому випадку
. Зрозуміло, що в розглянутому випадку  .
. , в якій
, в якій .
. .
. з деякого досить малого околу точки
з деякого досить малого околу точки  .
. справджуватимуться нерівності
справджуватимуться нерівності при
при  ,
, .
. , для якого справедливі нерівності
, для якого справедливі нерівності при
при  при
при  ,
, . Тоді границя відношення, яке стоїть в лівій частині нерівностей, існує і дорівнює похідній
. Тоді границя відношення, яке стоїть в лівій частині нерівностей, існує і дорівнює похідній  , тому
, тому ,
,  .
. .
.
 , в якій справджуються рівність
, в якій справджуються рівність . (6.73)
. (6.73) ,
, на відрізку
на відрізку 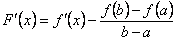 ;
; .
. або, що саме,
або, що саме,

 є кутовий коефіцієнт січної
є кутовий коефіцієнт січної  , а
, а  , то можемо записати:
, то можемо записати: .
.
 ,
, .
. , одержимо рівність
, одержимо рівність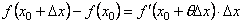 .
. функції в точці
функції в точці  . Отже, дістаємо формулу
. Отже, дістаємо формулу . (6.74)
. (6.74) і має назву формули скінчених приростів.
і має назву формули скінчених приростів. має похідні
має похідні 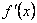 і
і  за будь-якого
за будь-якого  , то
, то  Тоді функція
Тоді функція  задовольняє умовам теореми Лагранжа і справедливою є рівність
задовольняє умовам теореми Лагранжа і справедливою є рівність .
. при будь-якому
при будь-якому  , дорівнює нулю. Тоді з попередньої нерівності випливає:
, дорівнює нулю. Тоді з попередньої нерівності випливає:  , або
, або  .
. і
і  - довільні точки проміжку
- довільні точки проміжку  на проміжку
на проміжку  і за будь-якого
і за будь-якого  , то різниця між цими функціями
, то різниця між цими функціями  є величина стала.
є величина стала.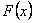 :
:  .
.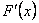 :
: .
. , тому
, тому  . Звідси випливає, що
. Звідси випливає, що  або, що те саме,
або, що те саме,  .
. , що має місце рівність
, що має місце рівність . (6.75)
. (6.75)
 - довільні дійсні числа, які називаються коефіцієнтами многочлена.
- довільні дійсні числа, які називаються коефіцієнтами многочлена. та його похідні.
та його похідні.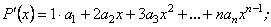


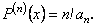
 , дістаємо
, дістаємо



 (6.76)
(6.76) , де
, де  - довільне дійсне число:
- довільне дійсне число:
 - дійсні числа. Тоді многочлен
- дійсні числа. Тоді многочлен  (6.77)
(6.77) і в самій точці
і в самій точці  має похідні до
має похідні до  -го порядку включно.
-го порядку включно. (6.78)
(6.78)

 залежить від
залежить від  то й
то й  залежить від
залежить від 

 (6.79)
(6.79) а функція
а функція  Виразимо
Виразимо  -го порядку від функції
-го порядку від функції  точки
точки 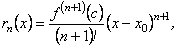 (6.80)
(6.80)
 (6.81)
(6.81)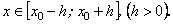
 , то матимемо так звану формулу Маклорена
, то матимемо так звану формулу Маклорена (6.82)
(6.82) (6.83)
(6.83) має в околі точки
має в околі точки  неперервні частинні похідні до
неперервні частинні похідні до  (6.84)
(6.84)
 називається δ-околом точки Р0(х01; х02;…х0n).
називається δ-околом точки Р0(х01; х02;…х0n).



