
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Основні поняття та означення функції багатьох змінних.Содержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Способи задання функції. Область визначення. Графіки. Лінії рівня. На практиці досить часто функція y залежить не від однієї змінної x, а від багатьох аргументів x 1,…, x n. Означення. Множина значень { x 1,…, x n}, за яких вираз f (x 1,…, x n) має зміст, називається областю визначення функції від n змінних y = f (x 1,…, x n). Приклади. 1. Функція від двох змінних z =3 x +5 xy + y 2. Область визначення цієї функції - всі пари дійсних чисел (x; y). 2. Функція від чотирьох змінних y =2 x 1+3 x 2- x 3+7 x 4. 3. Функція від трьох змінних V=V (a, b, c)= a×b×c. Об’єм паралелепіпеда є функцією від довжин його сторін. 4. Функція від двох змінних Q = F (K, L). Обсяг випущеної продукції Q є функцією від кількості затраченого капіталу K та кількості затраченої праці L. Областю визначення цієї функції є множина { K ³0; L ³0}. 5. Область визначення функції
z
x Рис. 6.1. Функції від двох змінних геометрично зображають також за допомогою ліній рівня (ліній однакового рівня, ізоліній). Означення. Лінією рівня функції від двох змінних z = f (x, y) називається множина точок площин OXY таких, що f (x, y)=const= C. Прикладом ізоліній є паралелі та меридіани. Приклади. 1. Побудуємо лінії однакового рівня функції При C =6 отримуємо При C =8 отримуємо ізолінію (неявну функцію y від x) x 2+ y 2=62.
6 8 10 x Рис. 6.2. 2. Для випуску продукції Q використовують ресурси x 1 та x 2. Виробнича функція має вигляд Q =10 x 1+20 x 2 (ресурси повністю взаємозамінні, наприклад, цвяхи та шурупи). Зобразити ізолінії для Q=Q (x 1, x 2) (лінії однакової кількості (quantity) продукції, ізокванти). Очевидно, що при C =60 ізолінія (ізокванта) – це відрізок прямої 10 x 1+20 x 2=60, а при C =40 – відрізок прямої 10 x 1+20 x 2=40 (рис. 6.3).
(Ресурс x 1)
Рис. 6.3. 3. Виробнича функція має вигляд Q =min{10 x 1,20 x 2} (ресурси повністю взаємодоповнюючі, наприклад, калійні та азотні добрива).
Тоді в точках (x 1=2, x 2=1), (x 1=4, x 2=1), (x 1=2, x 2=3) значення Q =40. У точках (x 1=4; x 2=2) та (x 1=4; x 2=4) випуск набуває значення Q =80. На рис. 6.4 зображені лінії однакового рівня (ізокванти) для кількості продукції Q.
1 2 3 4 5 (Ресурс x 2)
Рис. 6.4.
Зазначимо, що в другому та третьому прикладах зобразити функцію Q=Q (x 1, x 2) геометрично в тривимірному просторі дуже складно.
Похідна за напрямом. Градієнт. Нехай функція z=f(x;y) визначена на деякому околі т. Р0(х0;у0); l - деякий промінь з початком у точці Р0(х0;у0); Р(х;у) – точка на цьому промені, яка належить околу, що розглядається Dl- довжина відрізка Р0Р.
Границя
Похідна характеризує швидкість змінювання функції у точці Р0(х0;у0) за напрямом
Вектор з координатами
Частинні похідні та диференціали Вищих порядків. Для функцій двох та багатьох змінних Частинною похідною функції
де Повним диференціалом функції багатьох змінних називається головна лінійна частина приросту функції. Для функції
Повний диференціал функції багатьох змінних застосовується до наближених обчислень, вважаючи, що Частинні похідні знаходяться за правилами та формулами диференціювання функції однієї змінної, вважаючи решту змінних сталими величинами. Частинною похідною n-го порядку функції багатьох змінних по одній змінній називають першу похідну від
Приклад. Знайти частинні похідні другого порядку функції
Розв’язання. Знайдемо частинні похідні першого порядку по кожній змінній:
Від кожної частинної похідної першого порядку
Мішані похідні, які відрізняються порядком диференціювання,
Приклад. Знайти Розв’язання. Знайдемо частинну похідну функції тільки по
Задача. Знайти рівняння прямої
Розв’язання. Згідно методу найменших квадратів для знаходження параметрів
Для простоти складання системи (34) складемо таблицю значень:
Відповідь. Рівняння прямої має вигляд
Неявні функції. Похідні неявних функцій. Частинні похідні неявної функції
Знайти похідну а)
Знайдемо частинні похідні: За формулою (2.7) маємо: б)
За формулою (2.7) маємо: Нехай потрібно знайти похідну
звідки Приклад. Знайти похідну Маємо
звідки
|
||||||||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 612; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 3.147.103.204 (0.011 с.) |

 визначається з нерівності 100- x 2- y 2³0, тобто x 2+ y 2£102. Це круг з центром у початку координат і радіусом r = 10.
визначається з нерівності 100- x 2- y 2³0, тобто x 2+ y 2£102. Це круг з центром у початку координат і радіусом r = 10. Функція від двох змінних (аргументів) f(x, y) представляє собою деяку поверхню в трьохвимірному просторі. Зокрема, графіком функції
Функція від двох змінних (аргументів) f(x, y) представляє собою деяку поверхню в трьохвимірному просторі. Зокрема, графіком функції  є верхня половина сфери (рис. 6.1).
є верхня половина сфери (рис. 6.1).


 6 8 10 y
6 8 10 y . При C =0 маємо
. При C =0 маємо  тобто x 2+ y 2=102 (коло з радіусом r =10, рис.6.2).
тобто x 2+ y 2=102 (коло з радіусом r =10, рис.6.2). тобто x 2+ y 2=82. Отже лінією рівня, яка відповідає константі C =6, є коло з радіусом r = 8.
тобто x 2+ y 2=82. Отже лінією рівня, яка відповідає константі C =6, є коло з радіусом r = 8.
 y
y

 4 Q =60
4 Q =60 3
3
 2 Q =40
2 Q =40 1
1 1 2 3 4 5 6 (Ресурс x 2)
1 2 3 4 5 6 (Ресурс x 2) (Ресурс x 1)
(Ресурс x 1)
 5
5

 2 Q =80
2 Q =80

 1 Q =40
1 Q =40
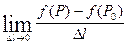 , якщо вона існує, називається похідною за напрямом.
, якщо вона існує, називається похідною за напрямом. .
.
 , який характеризує напрям максимального зростання функції z=f(x;y) у точці Р0(х0;у0), називається градієнтом у цій точці
, який характеризує напрям максимального зростання функції z=f(x;y) у точці Р0(х0;у0), називається градієнтом у цій точці  .
. ,
,  розглянемо частинні похідні.
розглянемо частинні похідні.
 та
та  – частинний приріст функції по одній змінній.
– частинний приріст функції по одній змінній.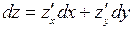 .
. .
. -ї похідної.
-ї похідної. .
.
 та
та  знайдемо першу похідну по кожній змінній. Це будуть частинні похідні другого порядку і їх буде чотири:
знайдемо першу похідну по кожній змінній. Це будуть частинні похідні другого порядку і їх буде чотири:
 , рівні між собою. Ця умова виконується у випадку їх неперервності.
, рівні між собою. Ця умова виконується у випадку їх неперервності. , якщо
, якщо  .
.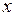 або по
або по  , а потім від неї знайдемо першу похідну по іншій змінній. Одержимо
, а потім від неї знайдемо першу похідну по іншій змінній. Одержимо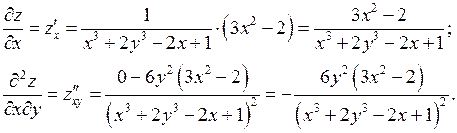
 методом найменших квадратів, користуючись таблицею значень
методом найменших квадратів, користуючись таблицею значень .
. і
і 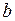 прямої використовують систему рівнянь:
прямої використовують систему рівнянь: (34)
(34)

 .
. , заданої рівнянням
, заданої рівнянням  , можуть бути обчисленні за формулами:
, можуть бути обчисленні за формулами: ,
,  . (2.8)
. (2.8) від функцій, заданих неявно:
від функцій, заданих неявно: .
.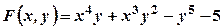 .
. ,
,  .
. .
. .
. .
. ,
,  .
. .
. у тому випадку, коли функція
у тому випадку, коли функція  задана неявно у вигляді
задана неявно у вигляді  . Узявши від функції F (x, y) повний диференціал, отримуємо
. Узявши від функції F (x, y) повний диференціал, отримуємо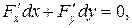
 .
. якщо
якщо 

 .
.


