
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Найбільше і найменше значення функції в замкненій областіСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Для знаходження найбільшого і найменшого значень функцій у замкненій області ä Приклад. Знайти екстремум функції Знаходимо частинні похідні
Стаціонарні точки функції визначимо із системи:
Додаючи ці рівняння, знайдемо Підставляючи Отже, функція має три стаціонарні точки:
Знайдемо величину
то
Обчислимо величину
Таким чином, точки У точці Переконаємося, що в цій точці екстремум відсутній. Якщо Якщо ä Приклад. Знайти найбільше і найменше значення функції Спочатку знайдемо критичні точки всередині області:
Згідно з необхідними умовами існування екстремуму функції двох змінних маємо систему рівнянь
Всередині області
В критичній точці Тепер проведемо дослідження функції на межі трикутника. На прямій
Знайдемо найбільше та найменше значення цієї функції однієї змінної х на замкненому відрізку Із рівності При На прямій Отже, задана функція Найбільше значення найменше значення 6. Умовний екстремум функції багатьох змінних. Метод множників Лагранжа та його застосування в економіко-математичних моделях планування виробництва
Нехай в області Задача полягає в тому, щоб на лінії Умовні екстремуми часто використовуються при дослідженні оптимізації багатьох економічних та соціальних проблем. Для знаходження умовного екстремуму скористаємося методом множників Лагранжа. 1) Записати функцію Лагранжа вигляду
2) Знайти критичні точки
3) Перевірити в кожній критичній точці достатні умови існування екстремуму: а) знайти
б) встановити знак, знайденого диференціала: якщо в точці якщо в точці 4) Знайти значення функції у точках екстремуму.
Для функції
Стаціонарні точки умовного екстремуму знаходяться із системи рівнянь
а достатні умови існування умовного екстремуму в цих точках можна визначити за знаком диференціала
ä Приклад. Дослідити на умовний екстремум методом множників Лагранжа функцію
Складемо функцію Лагранжа
Знайдемо її частинні похідні за всіма змінними
Розв’яжемо дану систему за допомогою оберненої матриці:
Отже, за формулою оберненої матриці:
Отже, шуканий результат:
Отже, Точка Знайдемо повний диференціал другого порядку функції Лагранжа.
Отже, точка
$$$ Аналіз задач з економіки за допомогою виробничих функцій Важливим елементом мікро- та макроекономічної теорії раціонального ведення господарства є, з одного боку, виробник, який витрачає економічні ресурси для виготовлення продукції і послуг, а з іншого – технологічні процеси, пов’язані з виробництвом. У бізнесі маргінальною продуктивністю виробництва називають гранично можливу продуктивність при умові постійного відтворювання виробництва. Кількість та якість кінцевого випуску будь-якої продукції фірми залежить від багатьох факторів, які фірма може змінювати. Найбільш важливі фактори – продуктивність праці та вкладений у виробництво капітал. При вивченні економічних процесів у сучасному великомасштабному виробництві буває надзвичайно важко зібрати необхідну інформацію для побудови моделі, яка враховує внутрішні особливості виробництва. Подібні міркування лежать в основі теорії виробничих функцій. У ній була здійснена спроба визначити емпіричним способом вплив витраченого капіталу і праці на обсяг випущеної продукції переробною промисловістю. Ставилися задачі: 1) визначити клас функцій, який найкраще описує співвідношення між трьома вибраними характеристиками виробничої діяльності; 2) знайти числові параметри, що задають конкретну функцію; 3) порівняти одержані результати з фактичними даними. Д. Кобб запропонував функцію вигляду Такий вибір функції був зумовлений такими причинами: 1) з нелінійних функцій вона є однією з найпростіших і логарифмуванням зводиться до лінійної; 2) вона враховує нульовий ефект виробництва, тобто якщо один із чинників дорівнює нулю, то й виробнича функція дорівнює нулю. Економічно це означає, що не витрачаючи жодного з видів фондів, не одержимо продукції. Для того, щоб дати означення виробничої функції, введемо простір витрат
Припустимо, що компоненти вектора Функцію, що описує технологічний зв’язок між випуском продукції і витратами, називають виробничою функцією. Вона задає відображення будь-якого вектора витрат у невід’ємне число – максимальний випуск продукції. Припустимо також, що виробнича функція неперервно двічі диференційована. Таке її означення легко допускає узагальнення на випуск кількох видів продукції. У цьому випадку виробнича функція – це відображення, що моделює випуск т видів продукції у виробничому процесі з використанням п видів сировини. Для конкретності розглянемо двофакторну виробничу функцію
де Функцію У деяких випадках У загальних випадках Частинну похідну першого порядку Прибутки виробництва зростають, якщо
У теорії ймовірностей виробничі функції ототожнюють з кореляційними. Це зумовлено тим, що в задачах з економіки доводиться аналізувати значну сукупність статистичних даних, що спостерігаються протягом деякого періоду. Виробничі функції застосовують для аналізу ефективності використання ресурсів. За підсумковий показник часто беруть такі економічні величини, як прибуток, собівартість, випуск продукції тощо, як чинники вибирають витрати праці, засоби виробництва, застосування потужностей і т.д. Економічний аналіз виробничого процесу за допомогою виробничої функції здійснюється з урахуванням таких економічних категорій: 1) середніх і граничних значень ефективності; 2) коефіцієнтів еластичності; 3) коефіцієнтів заміщення. Середні показники ефективності визначаються за формулою
Для функції (4) такими будуть середня продуктивність праці Поряд із середніми характеристиками функції (4) важливу роль відіграють також граничні характеристики, які виражаються частинними похідними першого порядку і називаються граничними продуктами:
Так, гранична продуктивність праці
Оскільки Названі характеристики є розмірними величинами, пов’язаними з абсолютними приростами. Обмеження, що накладаються на другі похідні, виділяють опуклу підмножину економічної області G М атриця Гессе – це матриця виду
Матриця Гессе додатно визначена, якщо
від’ємно визначена для усіх х, тобто
Співвідношення (6) називають законом спадної віддачі. Витрати одного виду додаються до фіксованих обсягів інших витрат. У кінцевому випадку досягається особлива область, де граничний продукт витрат знижується. Виробнича функція в області, де виконуються умови (6) і (8), характеризується прибутком від розширення масштабів виробництва і „можливостями заміщення”, тобто вказує поведінку випуску продукції, коли всі витрати змінюються в однаковій пропорції. Припустимо, що в деякій точці х усі витрати множаться на число а, тобто
У першому випадку виробнича функція характеризується постійним прибутком від розширення виробництва. Так, підвищення всіх витрат у 3 рази збільшить кінцеву продукцію також у 3 рази. У двох інших випадках вона зростає повільніше або швидше, ніж масштаби виробництва. Локальним показником вимірювання доходу від розширення виробництва є еластичність виробництва
Частинні коефіцієнти еластичності випуску відносно витрат Коефіцієнти еластичності характеризують відсоток приросту продукції при збільшенні витрат ресурсу на 1%. Так. Для функції (4) коефіцієнт еластичності
Нехай приріст Особливістю реальних виробничих процесів є можливість заміщення одного чинника іншим. Необхідність заміни одного чинника іншим пов’язана з тим, що він може бути дефіцитним і тому виникає потреба замінити його більш доступним. Граничною нормою заміщення чинників називають відношення
Локальною мірою заміщення двох чинників, наприклад
Так як при малих приростах аргументу ??? Контрольні питання 1. Що називається функцією двох змінних? 2. Що називається областю визначення функції? 3. Що називається функцією трьох змінних? 4. Що називається функцією п змінних? 5. Що називається границею функції 6. Що називається лінією рівня функції 7. Сформулювати означення неперервної функції двох змінних в точці і на множині точок. 8. Що називається замкненою обмеженою областю? 9. Яку функцію називають функцією Кобба-Дугласа? 10.Що називається частинною похідною функції двох змінних по одній з них? 11. Як визначають частинні похідні другого і третього порядку від функції двох змінних? 12. Сформулювати теорему про рівність других мішаних похідних. 13. Яка функція 14. Сформулювати достатні умови диференційованості функції двох змінних. 15. Що називається повним диференціалом функції двох, п змінних? 16. Як визначають диференціал п -го порядку? 17. Як знаходять похідну складної функції 18. Що називається повною похідною? 19. Які точки називаються точками локального екстремуму? 20. Сформулювати необхідні та достатні умови локального екстремуму функції кількох змінних. 21. Що таке умовний екстремум? 22. Що називається найбільшим і найменшим значенням функції багатьох змінних? 23. Описати спосіб знаходження умовного екстремуму. 24. Що називається функцією Лагранжа? 25. В чому полягає метод множників Лагранжа? 26. Що таке виробнича функція? 27. Яку залежність називають кореляційною? 28. За допомогою чого проводять економічний аналіз виробничого процесу? 29. Що таке економічна область? 30. Що називають граничними продуктами? 31. Що таке еластичність виробництва? 32. Що таке гранична норма заміщення чинників?
|
||
|
Последнее изменение этой страницы: 2016-12-12; просмотров: 1367; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.119 (0.011 с.) |

 , які позначаються
, які позначаються  і
і  , відповідно, необхідно знайти екстремальні значення функції в точках, що лежать всередині
, відповідно, необхідно знайти екстремальні значення функції в точках, що лежать всередині 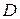 та на межі області, і обрати найбільше і найменше значення.
та на межі області, і обрати найбільше і найменше значення.


 , звідки
, звідки  .
. , звідки
, звідки 
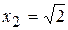 ,
,  , тоді
, тоді 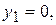
 ,
, 
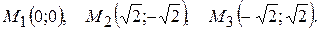
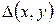 . Оскільки
. Оскільки



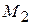 і
і  – точки мінімуму. В цих точках
– точки мінімуму. В цих точках 
 значення
значення  , тому скористатися теоремою про існування екстремуму не можна.
, тому скористатися теоремою про існування екстремуму не можна. , то
, то  в околі точки
в околі точки  , то
, то  . Отже, в околі точки
. Отже, в околі точки  можуть бути як додатні, так і від’ємні, а це значить, що точка
можуть бути як додатні, так і від’ємні, а це значить, що точка  в трикутнику, обмеженому лініями
в трикутнику, обмеженому лініями 



 , тому
, тому
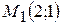 маємо
маємо 
 змінна
змінна  і функція
і функція 

 знаходимо:
знаходимо:  , звідси випливає, що
, звідси випливає, що  та
та  Отже,
Отже, 
 та
та 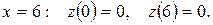

 на межі області.
на межі області.

 і лінію
і лінію  , яка визначається рівнянням
, яка визначається рівнянням  та лежить в цій області.
та лежить в цій області. , в якій значення функції
, в якій значення функції  є найбільшим або найменшим порівняно із значеннями цієї функції в інших точках лінії
є найбільшим або найменшим порівняно із значеннями цієї функції в інших точках лінії  .
. функції Лагранжа, використовуючи необхідні умови існування екстремуму:
функції Лагранжа, використовуючи необхідні умови існування екстремуму:

 :
:
 , то ця точка є точкою умовного мінімуму,
, то ця точка є точкою умовного мінімуму, , то ця точка є точкою умовного максимуму.
, то ця точка є точкою умовного максимуму. з рівняннями
з рівняннями  та
та  функція Лагранжа запишеться у вигляді
функція Лагранжа запишеться у вигляді .
.

 при заданих обмеженнях
при заданих обмеженнях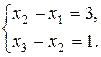

 та прирівняємо їх до нуля.
та прирівняємо їх до нуля.
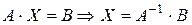 .
. .
.

 .
.

 – екстремальна точка.
– екстремальна точка.

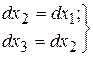 з диференціювання обмежень.
з диференціювання обмежень.
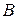 – точка мінімуму.
– точка мінімуму.

 , де
, де  – обсяг випущеної продукції,
– обсяг випущеної продукції,  – обсяг основного капіталу,
– обсяг основного капіталу,  – числові параметри, що задовольняють умову
– числові параметри, що задовольняють умову  .
. – кількість витрат
– кількість витрат  -го виду. Вектор витрат
-го виду. Вектор витрат . Тоді
. Тоді  .
. змінюються неперервно. Тоді кожній точці простору витрат можна поставити у відповідність (максимальний) випуск продукції, виготовленої з використанням цих витрат.
змінюються неперервно. Тоді кожній точці простору витрат можна поставити у відповідність (максимальний) випуск продукції, виготовленої з використанням цих витрат. , (4)
, (4) – кінцевий результат, наприклад, кількість одиниць випущеної фірмою продукції,
– кінцевий результат, наприклад, кількість одиниць випущеної фірмою продукції, 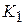 ), яке дозволило скоротити кількість праці у три рази. У цьому прикладі можна встановити функціональну залежність між
), яке дозволило скоротити кількість праці у три рази. У цьому прикладі можна встановити функціональну залежність між  називають граничною продуктивністю праці при фіксованому
називають граничною продуктивністю праці при фіксованому  називають граничною продуктивністю капіталу при фіксованій продуктивності праці
називають граничною продуктивністю капіталу при фіксованій продуктивності праці  .
.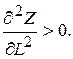
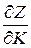 характеризує зміну випуску продукції при постійних трудових затратах.
характеризує зміну випуску продукції при постійних трудових затратах. . (5)
. (5) і середня фондовіддача
і середня фондовіддача  . За означенням середня продуктивність праці є відношенням обсягу виробленої продукції до кількості витраченої праці, а середня фондовіддача – відношенням обсягу виробленої продукції до основних фондів. Зокрема, для функції
. За означенням середня продуктивність праці є відношенням обсягу виробленої продукції до кількості витраченої праці, а середня фондовіддача – відношенням обсягу виробленої продукції до основних фондів. Зокрема, для функції  така залежність є спадною функцією вартості виробленої продукції
така залежність є спадною функцією вартості виробленої продукції  , що виражає обсяг основних фондів, який припадає на одного працюючого.
, що виражає обсяг основних фондів, який припадає на одного працюючого. .
. характеризує додатковий ефект від кожної витраченої додаткової одиниці праці в заданій точці
характеризує додатковий ефект від кожної витраченої додаткової одиниці праці в заданій точці  фазової площини. Для функції Кобби-Дугласа
фазової площини. Для функції Кобби-Дугласа .
. , гранична продуктивність праці пропорційна середній продуктивності праці з коефіцієнтом
, гранична продуктивність праці пропорційна середній продуктивності праці з коефіцієнтом  і менша від неї. Те саме можна сказати також про граничну фондовіддачу.
і менша від неї. Те саме можна сказати також про граничну фондовіддачу. , стосовно якої матриця Гессе
, стосовно якої матриця Гессе . Головні мінори матриці мають вигляд
. Головні мінори матриці мають вигляд 

 ;...;
;...;  .
. – умови мінімуму; матриця від’ємно визначена, якщо
– умови мінімуму; матриця від’ємно визначена, якщо  – умови максимуму.
– умови максимуму. (7)
(7)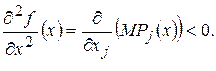 (8)
(8) . Можливі три різні випадки:
. Можливі три різні випадки: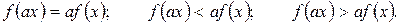 (9)
(9) . (10)
. (10) . Тоді
. Тоді  .
. . (11)
. (11) основних фондів при фіксованих трудових ресурсах дає приріст продукції
основних фондів при фіксованих трудових ресурсах дає приріст продукції  . Тоді збільшення основних фондів на
. Тоді збільшення основних фондів на  відповідає зміні випуску обсягу продукції на
відповідає зміні випуску обсягу продукції на  . Отже, при збільшенні обсягу основних фондів на 1% обсяг випуску зміниться на
. Отже, при збільшенні обсягу основних фондів на 1% обсяг випуску зміниться на  . Перейшовши до границі при
. Перейшовши до границі при  , матимемо формулу (11). Для функції Кобба-Дугласа коефіцієнти є сталими
, матимемо формулу (11). Для функції Кобба-Дугласа коефіцієнти є сталими  .
. .
. , коли решта витрат залишаються незмінними, може бути еластичність заміщення витрат
, коли решта витрат залишаються незмінними, може бути еластичність заміщення витрат  , що розраховується за формулою
, що розраховується за формулою
 має місце наближена рівність
має місце наближена рівність 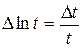 , приріст логарифма змінної величини можна розглядати як відносний приріст самої величини. Таким чином, величина обернена коефіцієнту еластичності заміщення, показує наближено, на скільки відсотків зміниться відношення граничних продуктів
, приріст логарифма змінної величини можна розглядати як відносний приріст самої величини. Таким чином, величина обернена коефіцієнту еластичності заміщення, показує наближено, на скільки відсотків зміниться відношення граничних продуктів  при зміні відношення затрат ресурсів
при зміні відношення затрат ресурсів  на 1%.
на 1%.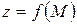 при
при  .
. ?
? ?
?


