Границя функції багатьох змінних
Функція. Графік функції
За аналогією з функцією змінної 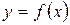 можна розглянути функцію, яка залежатиме від кількох незалежних змінних можна розглянути функцію, яка залежатиме від кількох незалежних змінних  . У загальному випадку . У загальному випадку
 . .
Означення. Якщо змінна величина  залежить від залежить від  незалежних змінних незалежних змінних  , то її називають функцією цих змінних, а функціональну залежність позначають так: , то її називають функцією цих змінних, а функціональну залежність позначають так:
 , або , або 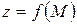 , де точка , де точка 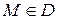 . .
Незалежні змінні  називають аргументами, а залежну змінну називають аргументами, а залежну змінну  – функцією. – функцією.
Означення. Сукупність усіх числових значень, які можуть приймати аргументи  і при яких функція і при яких функція  приймає певні дійсні значення, називають областю визначення функції і позначають приймає певні дійсні значення, називають областю визначення функції і позначають 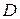 або або  . .
Якщо функція визначена для усіх  з деякої області з деякої області 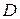 та її межі та її межі 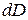 , тоді кажуть, що функція визначена у замкненій області , тоді кажуть, що функція визначена у замкненій області  . .
Множину значень  позначають позначають  або або  . .
Означення 11. Графіком функції  є деяка поверхня, яка проектується на площину є деяка поверхня, яка проектується на площину  в область визначення (рис.1). в область визначення (рис.1).
Часто використовується перетин поверхні  площиною площиною  . Криві лінії, які задовольняють умову . Криві лінії, які задовольняють умову  , називаються лініями рівня (ізолініями). , називаються лініями рівня (ізолініями).
 Областю визначення деякої функції Областю визначення деякої функції  є множина точок тривимірного простору, а множина значень – множина дійсних чисел (рис. 2). є множина точок тривимірного простору, а множина значень – множина дійсних чисел (рис. 2).
Функцію багатьох змінних можна задавати аналітично, таблично, графічно, за допомогою ліній рівня, мовно і за допомогою комп’ютерної програми.
ä Приклад. Знайти область визначення  даної функції даної функції  . .
Оскільки областю визначення функції  є множина є множина 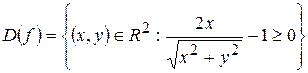 , то для її відшукання розв’язуємо нерівність , то для її відшукання розв’язуємо нерівність
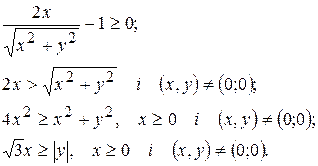
Отже,  . .
Множиною граничних точок є  , внутрішніх точок – , внутрішніх точок –  , межових точок – , межових точок –  . Ізольованих точок множина . Ізольованих точок множина  не має. не має.
Множина  не є замкненою, а, отже, і досконалою, оскільки точка не є замкненою, а, отже, і досконалою, оскільки точка 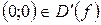 , але , але  . Множина . Множина  є відкритою, оскільки точки є відкритою, оскільки точки 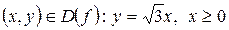 , не є внутрішніми для , не є внутрішніми для  . .
Портфель цінних паперів
Інший приклад кривих байдужості виникає в теорії інвестицій.
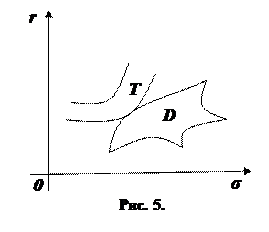 Портфель цінних паперів (під портфелем будемо розуміти сукупність визначених цінних паперів у визначених кількостях) характеризується двома основними параметрами – очікуваною дохідністю Портфель цінних паперів (під портфелем будемо розуміти сукупність визначених цінних паперів у визначених кількостях) характеризується двома основними параметрами – очікуваною дохідністю  і ризиком і ризиком  . Кожному портфелю можна поставити у відповідність точку на координатній площині . Кожному портфелю можна поставити у відповідність точку на координатній площині  , і тоді множина усіх можливих портфелів представляє деяку область , і тоді множина усіх можливих портфелів представляє деяку область 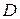 (рис. 5). (рис. 5).
Очевидно, що при рівних дохідностях інвестор надасть перевагу портфелю з меншим ризиком. Таким чином, криві байдужості – лінії рівня функції переваги  – опуклі вниз. Точка – опуклі вниз. Точка  , у якій лінія байдужості дотикається області , у якій лінія байдужості дотикається області 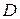 , відповідає найкращому портфелю для інвестора. , відповідає найкращому портфелю для інвестора.
Частинні похідні та диференціали першого порядку
Частинні похідні
Нехай функція  визначена в деякому околі точки визначена в деякому околі точки  . Надамо змінній . Надамо змінній  приросту приросту  , залишаючи змінну , залишаючи змінну 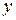 незмінною, так, щоб точка незмінною, так, щоб точка  належала заданому околу. належала заданому околу.
Означення. Величина

називається частинним приростом функції  по змінній х. по змінній х.
Аналогічно вводиться частинний приріст  функції по змінній функції по змінній 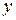 : :
 . .
Означення. Якщо існує границя
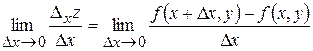 , ,
то вона називається частинною похідною першого порядку функції  в точці в точці  по змінній по змінній  і позначається одним із таких символів і позначається одним із таких символів
 ; ;
 – частинні похідні по х в точці – частинні похідні по х в точці 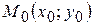 . .
Аналогічно частинна похідна першого порядку функції  по змінній по змінній 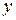 визначається як визначається як

і позначається одним із символів:
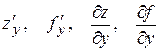 . .
Згідно з означенням, при знаходженні частинної похідної  обчислюють звичайну похідну функції однієї змінної х, вважаючи змінну обчислюють звичайну похідну функції однієї змінної х, вважаючи змінну 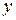 сталою, а при знаходженні похідної сталою, а при знаходженні похідної  сталою вважається змінна х. сталою вважається змінна х.
ä Приклад. Знайти частинні похідні функції  . .


ä Приклад. Потік пасажирів  виражається функцією виражається функцією 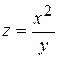 , де х – число мешканців, , де х – число мешканців, 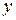 – відстань між містами. Знайти частинні похідні функції і пояснити їх зміст. – відстань між містами. Знайти частинні похідні функції і пояснити їх зміст.
Похідна  показує, що при одній і тій же відстані між містами збільшення потоку пасажирів пропорційне подвоєному числу мешканців. Похідна показує, що при одній і тій же відстані між містами збільшення потоку пасажирів пропорційне подвоєному числу мешканців. Похідна 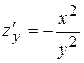 показує, що при одній і тій же чисельності мешканців збільшення потоку пасажирів обернено пропорційне квадрату відстані між містами. показує, що при одній і тій же чисельності мешканців збільшення потоку пасажирів обернено пропорційне квадрату відстані між містами.
Диференційована функція
Означення. Операція знаходження похідної  називається диференціюванням функції називається диференціюванням функції  по аргументу х, а точка по аргументу х, а точка  – точкою диференціювання. Операція знаходження похідної – точкою диференціювання. Операція знаходження похідної  називається диференціюванням функції називається диференціюванням функції  по аргументу по аргументу 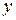 . .
Означення. Функція  називається диференційованою в точці називається диференційованою в точці  , якщо повний приріст даної функції в цій точці , якщо повний приріст даної функції в цій точці
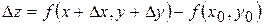
можна представити у вигляді
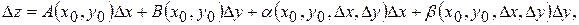
де  – дійсні числа, а функції – дійсні числа, а функції 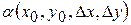 , ,  такі, що такі, що

Означення. Функція  називається диференційованою в області називається диференційованою в області 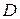 , якщо вона диференційована в кожній точці , якщо вона диференційована в кожній точці  цієї області. цієї області.
Теорема 1. Якщо функція 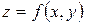 диференційована в точці диференційована в точці  , то вона неперервна в цій точці. , то вона неперервна в цій точці.
Теорема 2. Якщо функція 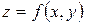 диференційована в точці диференційована в точці  , то в цій точці існують частинні похідні за змінними х та , то в цій точці існують частинні похідні за змінними х та 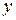 , до того ж , до того ж

Теорема 3. Якщо функція 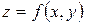 має частинні похідні в околі точки має частинні похідні в околі точки  , які неперервні в цій точці, то функція , які неперервні в цій точці, то функція  диференційована в точці диференційована в точці  . .
Повний диференціал функції
Означення.Повним диференціалом  функції двох змінних функції двох змінних 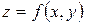 в точці в точці  називають головну частину повного приросту функції в даній точці, яка лінійно залежить від приростів незалежних змінних називають головну частину повного приросту функції в даній точці, яка лінійно залежить від приростів незалежних змінних  і і 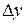 , тобто , тобто
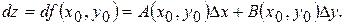
Повний диференціал  функції функції 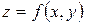 в точці в точці  , де , де 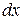 і і  – диференціали незалежних змінних, – диференціали незалежних змінних, 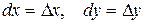 має вигляд: має вигляд:
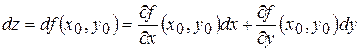
або
 . .
ä Приклад. Знайти повний приріст і повний диференціал функції 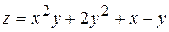 в точці в точці  , якщо , якщо 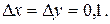
Оскільки 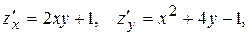
то  а а 
Повний приріст і повний диференціал функції в точці  обчислюватимемо за формулами: обчислюватимемо за формулами:
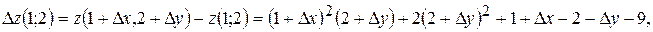 
Тоді різниця  являє собою похибку, яка виникає від заміни повного приросту являє собою похибку, яка виникає від заміни повного приросту  функції її повним диференціалом функції її повним диференціалом  . Маємо: . Маємо:



Функція. Графік функції
За аналогією з функцією змінної 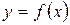 можна розглянути функцію, яка залежатиме від кількох незалежних змінних можна розглянути функцію, яка залежатиме від кількох незалежних змінних  . У загальному випадку . У загальному випадку
 . .
Означення. Якщо змінна величина  залежить від залежить від  незалежних змінних незалежних змінних  , то її називають функцією цих змінних, а функціональну залежність позначають так: , то її називають функцією цих змінних, а функціональну залежність позначають так:
 , або , або 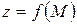 , де точка , де точка 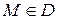 . .
Незалежні змінні  називають аргументами, а залежну змінну називають аргументами, а залежну змінну  – функцією. – функцією.
Означення. Сукупність усіх числових значень, які можуть приймати аргументи  і при яких функція і при яких функція  приймає певні дійсні значення, називають областю визначення функції і позначають приймає певні дійсні значення, називають областю визначення функції і позначають 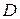 або або  . .
Якщо функція визначена для усіх  з деякої області з деякої області 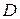 та її межі та її межі 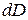 , тоді кажуть, що функція визначена у замкненій області , тоді кажуть, що функція визначена у замкненій області  . .
Множину значень  позначають позначають  або або  . .
Означення 11. Графіком функції  є деяка поверхня, яка проектується на площину є деяка поверхня, яка проектується на площину  в область визначення (рис.1). в область визначення (рис.1).
Часто використовується перетин поверхні  площиною площиною  . Криві лінії, які задовольняють умову . Криві лінії, які задовольняють умову  , називаються лініями рівня (ізолініями). , називаються лініями рівня (ізолініями).
 Областю визначення деякої функції Областю визначення деякої функції  є множина точок тривимірного простору, а множина значень – множина дійсних чисел (рис. 2). є множина точок тривимірного простору, а множина значень – множина дійсних чисел (рис. 2).
Функцію багатьох змінних можна задавати аналітично, таблично, графічно, за допомогою ліній рівня, мовно і за допомогою комп’ютерної програми.
ä Приклад. Знайти область визначення  даної функції даної функції  . .
Оскільки областю визначення функції  є множина є множина 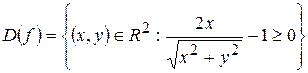 , то для її відшукання розв’язуємо нерівність , то для її відшукання розв’язуємо нерівність
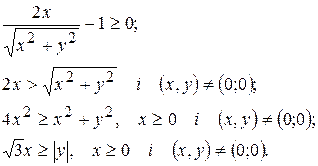
Отже,  . .
Множиною граничних точок є  , внутрішніх точок – , внутрішніх точок –  , межових точок – , межових точок –  . Ізольованих точок множина . Ізольованих точок множина  не має. не має.
Множина  не є замкненою, а, отже, і досконалою, оскільки точка не є замкненою, а, отже, і досконалою, оскільки точка 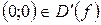 , але , але  . Множина . Множина  є відкритою, оскільки точки є відкритою, оскільки точки 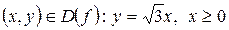 , не є внутрішніми для , не є внутрішніми для  . .
Границя функції багатьох змінних
Нехай точка  є точкою скупчення для області визначення є точкою скупчення для області визначення  функції функції  , а , а  – довільна точка множини – довільна точка множини  . .
Означення. Околом радіуса  точки точки  називають сукупність усіх точок називають сукупність усіх точок  простору простору  , відстань яких до точки , відстань яких до точки 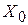 менше або дорівнює менше або дорівнює  , тобто виконується співвідношення , тобто виконується співвідношення

Означення. Число  називають границею функції називають границею функції  в точці в точці 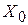 , або границею функції для , або границею функції для  , ,  ..., ...,  , якщо для будь-якого , якщо для будь-якого 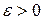 існує таке існує таке  , що з виконання нерівностей , що з виконання нерівностей


...............,

випливає виконання нерівності

Це записується так:

або

Означення. Число  називають границею функції називають границею функції  в точці в точці 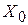 , якщо для будь-якого малого , якщо для будь-якого малого 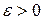 існує число існує число  таке, що із виконання нерівності таке, що із виконання нерівності

випливає справедливість нерівності

що записують

Означення (за Гейне). Число  називають границею функції називають границею функції  в точці в точці  , якщо для будь-якої послідовності , якщо для будь-якої послідовності  точок точок  , що збігається до точки , що збігається до точки 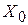 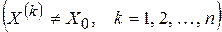 , послідовність відповідних значень функції , послідовність відповідних значень функції  , тобто , тобто  , ,  ,..., ,...,  , завжди збігається до числа , завжди збігається до числа  , що записують , що записують
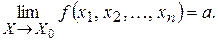
Теорема. Якщо  , ,  , ,  і і   то: то:
1) 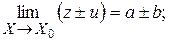
2) 
3)  (якщо (якщо  ). ).
ä Приклад. Для даної функції 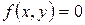 і і  , якщо , якщо  та точки та точки  визначити, чи існують границя функції в точці та повторні границі. визначити, чи існують границя функції в точці та повторні границі.
Нехай  . Тоді . Тоді  . Якщо . Якщо  , то , то  , оскільки множник , оскільки множник  , а множник , а множник  обмежений. Отже, обмежений. Отже, 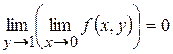 . Якщо . Якщо  , то , то  , а якщо , а якщо 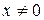 , то , то  не має границі при не має границі при  . Тому повторна границя . Тому повторна границя  не існує. Разом з тим не існує. Разом з тим 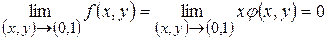 , оскільки множник , оскільки множник  , а функція , а функція

є обмеженою.
2. Неперервність функції багатьох змінних
Означення. Функція  називається неперервною в точці називається неперервною в точці  , якщо границя даної функції в точці , якщо границя даної функції в точці 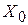 існує і дорівнює значенню функції в точці існує і дорівнює значенню функції в точці 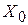 , тобто , тобто

незалежно від способу прямування точки  до точки до точки 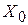 . .
Означення. Функція  називається неперервною в деякій області п -вимірного евклідового простору, якщо вона неперервна в кожній точці цієї області. називається неперервною в деякій області п -вимірного евклідового простору, якщо вона неперервна в кожній точці цієї області.
Означення. Якщо в точці  функція функція  не є неперервною, то вона називається розривною в цій точці, а точка не є неперервною, то вона називається розривною в цій точці, а точка 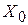 називається точкою розриву функції. називається точкою розриву функції.
Означення. Точки, в яких функція  неперервна, називаються точками неперервності. неперервна, називаються точками неперервності.
Властивості неперервних функцій двох змінних в замкненій обмеженій області:
1. Якщо функція  неперервна в замкненій обмеженій області, то вона обмежена в цій області, тобто існує таке число неперервна в замкненій обмеженій області, то вона обмежена в цій області, тобто існує таке число  , що для усіх точок області виконується нерівність , що для усіх точок області виконується нерівність 
2. Якщо функція  неперервна в замкненій обмеженій області, то в цій області існують точки, в яких функція набуває найбільшого і найменшого значень. неперервна в замкненій обмеженій області, то в цій області існують точки, в яких функція набуває найбільшого і найменшого значень.
3. Якщо функція  неперервна в замкненій обмеженій області неперервна в замкненій обмеженій області 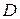 і і 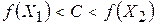 , де , де 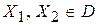 , то існує точка , то існує точка  , в якій , в якій  Зокрема, якщо Зокрема, якщо  , а , а  , то в області , то в області 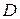 існує точка існує точка 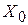 , в якій , в якій 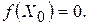
Теорема. Якщо  і і 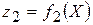 неперервні в точці неперервні в точці 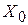 , то: , то:
а)  – неперервна в точці – неперервна в точці 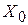 , ,
б) 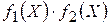 – неперервна в точці – неперервна в точці 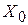 , ,
в)   – неперервна в точці – неперервна в точці 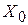 . .
ä Приклад. Знайти точки розриву функції  . .
Функція втратить зміст, якщо знаменник перетвориться в нуль. Але 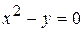 або або  – рівняння параболи. Отже, дана функція має лінією розриву параболу – рівняння параболи. Отже, дана функція має лінією розриву параболу  . .
3. Економічна область. Задачі про оптимальний розподіл ресурсів. Функції корисності
Значна частина економічних механізмів ілюструється на рисунках, які зображають лінії рівня функції двох змінних  . Наприклад, лінії рівня виробничої функції називаються ізоквантами. . Наприклад, лінії рівня виробничої функції називаються ізоквантами.
 Нехай Нехай  і і 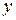 – два різних фактори виробництва, а функція – два різних фактори виробництва, а функція  характеризує випуск продукції, який дозволяють значення факторів характеризує випуск продукції, який дозволяють значення факторів  і і 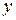 . На рис.3 лінії рівня . На рис.3 лінії рівня  зображені суцільними лініями, а штриховими виділена так звана економічна область, яка характеризується тим, що частини ізоквант, які вона відсікає, представляють собою графіки спадних функцій, тобто збільшення кількості одного фактора дозволяє зменшувати кількість другого, не змінюючи розміру випуску. зображені суцільними лініями, а штриховими виділена так звана економічна область, яка характеризується тим, що частини ізоквант, які вона відсікає, представляють собою графіки спадних функцій, тобто збільшення кількості одного фактора дозволяє зменшувати кількість другого, не змінюючи розміру випуску.
Означення. Множину значень факторів, які допускають заміщення одного з них іншим, називають економічною областю.
|



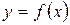 можна розглянути функцію, яка залежатиме від кількох незалежних змінних
можна розглянути функцію, яка залежатиме від кількох незалежних змінних  . У загальному випадку
. У загальному випадку .
. залежить від
залежить від  незалежних змінних
незалежних змінних  , то її називають функцією цих змінних, а функціональну залежність позначають так:
, то її називають функцією цих змінних, а функціональну залежність позначають так: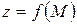 , де точка
, де точка 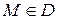 .
. називають аргументами, а залежну змінну
називають аргументами, а залежну змінну 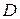 або
або  .
.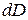 , тоді кажуть, що функція визначена у замкненій області
, тоді кажуть, що функція визначена у замкненій області  .
. або
або  .
. є деяка поверхня, яка проектується на площину
є деяка поверхня, яка проектується на площину  в область визначення (рис.1).
в область визначення (рис.1). . Криві лінії, які задовольняють умову
. Криві лінії, які задовольняють умову  , називаються лініями рівня (ізолініями).
, називаються лініями рівня (ізолініями). Областю визначення деякої функції
Областю визначення деякої функції  .
. є множина
є множина 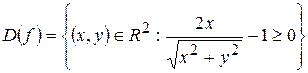 , то для її відшукання розв’язуємо нерівність
, то для її відшукання розв’язуємо нерівність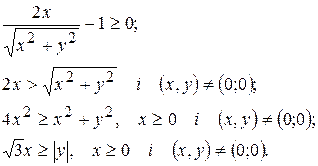
 .
. , внутрішніх точок –
, внутрішніх точок –  , межових точок –
, межових точок –  . Ізольованих точок множина
. Ізольованих точок множина 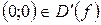 , але
, але  . Множина
. Множина  є відкритою, оскільки точки
є відкритою, оскільки точки 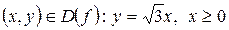 , не є внутрішніми для
, не є внутрішніми для 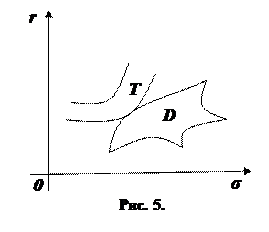 Портфель цінних паперів (під портфелем будемо розуміти сукупність визначених цінних паперів у визначених кількостях) характеризується двома основними параметрами – очікуваною дохідністю
Портфель цінних паперів (під портфелем будемо розуміти сукупність визначених цінних паперів у визначених кількостях) характеризується двома основними параметрами – очікуваною дохідністю  і ризиком
і ризиком  . Кожному портфелю можна поставити у відповідність точку на координатній площині
. Кожному портфелю можна поставити у відповідність точку на координатній площині  , і тоді множина усіх можливих портфелів представляє деяку область
, і тоді множина усіх можливих портфелів представляє деяку область  – опуклі вниз. Точка
– опуклі вниз. Точка  , у якій лінія байдужості дотикається області
, у якій лінія байдужості дотикається області  . Надамо змінній
. Надамо змінній  , залишаючи змінну
, залишаючи змінну 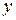 незмінною, так, щоб точка
незмінною, так, щоб точка  належала заданому околу.
належала заданому околу.
 по змінній х.
по змінній х. функції по змінній
функції по змінній  .
.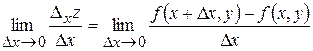 ,
, по змінній
по змінній  ;
; – частинні похідні по х в точці
– частинні похідні по х в точці 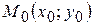 .
.
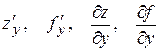 .
. обчислюють звичайну похідну функції однієї змінної х, вважаючи змінну
обчислюють звичайну похідну функції однієї змінної х, вважаючи змінну  сталою вважається змінна х.
сталою вважається змінна х. .
.

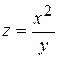 , де х – число мешканців,
, де х – число мешканців,  показує, що при одній і тій же відстані між містами збільшення потоку пасажирів пропорційне подвоєному числу мешканців. Похідна
показує, що при одній і тій же відстані між містами збільшення потоку пасажирів пропорційне подвоєному числу мешканців. Похідна 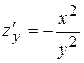 показує, що при одній і тій же чисельності мешканців збільшення потоку пасажирів обернено пропорційне квадрату відстані між містами.
показує, що при одній і тій же чисельності мешканців збільшення потоку пасажирів обернено пропорційне квадрату відстані між містами. – точкою диференціювання. Операція знаходження похідної
– точкою диференціювання. Операція знаходження похідної 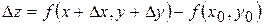
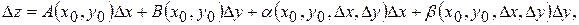
 – дійсні числа, а функції
– дійсні числа, а функції 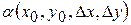 ,
,  такі, що
такі, що
 цієї області.
цієї області.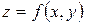 диференційована в точці
диференційована в точці 
 функції двох змінних
функції двох змінних 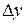 , тобто
, тобто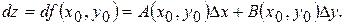
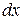 і
і  – диференціали незалежних змінних,
– диференціали незалежних змінних, 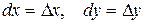 має вигляд:
має вигляд: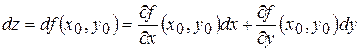
 .
.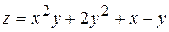 в точці
в точці  , якщо
, якщо 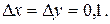
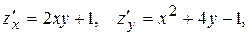
 а
а 
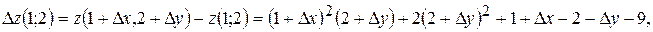

 являє собою похибку, яка виникає від заміни повного приросту
являє собою похибку, яка виникає від заміни повного приросту  функції її повним диференціалом
функції її повним диференціалом 


 є точкою скупчення для області визначення
є точкою скупчення для області визначення  – довільна точка множини
– довільна точка множини  , відстань яких до точки
, відстань яких до точки 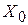 менше або дорівнює
менше або дорівнює 
 називають границею функції
називають границею функції  ,
,  ...,
...,  , якщо для будь-якого
, якщо для будь-якого 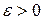 існує таке
існує таке  , що з виконання нерівностей
, що з виконання нерівностей





 в точці
в точці 


 точок
точок  , що збігається до точки
, що збігається до точки 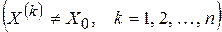 , послідовність відповідних значень функції
, послідовність відповідних значень функції  , тобто
, тобто  ,
,  ,...,
,...,  , завжди збігається до числа
, завжди збігається до числа 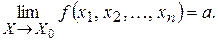
 ,
, 
 то:
то: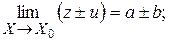

 (якщо
(якщо  ).
).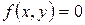 і
і  , якщо
, якщо  та точки
та точки  визначити, чи існують границя функції в точці та повторні границі.
визначити, чи існують границя функції в точці та повторні границі. . Тоді
. Тоді  . Якщо
. Якщо  , оскільки множник
, оскільки множник  , а множник
, а множник  обмежений. Отже,
обмежений. Отже, 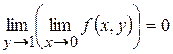 . Якщо
. Якщо  , то
, то  , а якщо
, а якщо 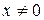 , то
, то  . Тому повторна границя
. Тому повторна границя  не існує. Разом з тим
не існує. Разом з тим 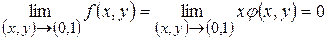 , оскільки множник
, оскільки множник 

 до точки
до точки  неперервна в замкненій обмеженій області, то вона обмежена в цій області, тобто існує таке число
неперервна в замкненій обмеженій області, то вона обмежена в цій області, тобто існує таке число  , що для усіх точок області виконується нерівність
, що для усіх точок області виконується нерівність 
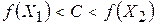 , де
, де 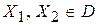 , то існує точка
, то існує точка  , в якій
, в якій  Зокрема, якщо
Зокрема, якщо  , а
, а  , то в області
, то в області 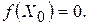
 і
і 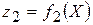 неперервні в точці
неперервні в точці  – неперервна в точці
– неперервна в точці 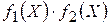 – неперервна в точці
– неперервна в точці 
 – неперервна в точці
– неперервна в точці  .
.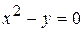 або
або  – рівняння параболи. Отже, дана функція має лінією розриву параболу
– рівняння параболи. Отже, дана функція має лінією розриву параболу  Нехай
Нехай  зображені суцільними лініями, а штриховими виділена так звана економічна область, яка характеризується тим, що частини ізоквант, які вона відсікає, представляють собою графіки спадних функцій, тобто збільшення кількості одного фактора дозволяє зменшувати кількість другого, не змінюючи розміру випуску.
зображені суцільними лініями, а штриховими виділена так звана економічна область, яка характеризується тим, що частини ізоквант, які вона відсікає, представляють собою графіки спадних функцій, тобто збільшення кількості одного фактора дозволяє зменшувати кількість другого, не змінюючи розміру випуску.


