
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неперервність функції в точці і на відрізкуСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте
Нехай у = Отже, При х = х1 маємо у, = Отже, Тепер можна перейти до поняття неперервності функції. Дамо два означення неперервності функції в точці, які досить часто використовуються. Означення 1. Якщо нескінченно малому прирісту аргументу Із цього означення випливає, що для дослідження неперервності функції в точці х = х0 достатньо впевнитись, що при Означення 2. Функцію у = 1) 2) існує скінченна границя 3) тобто Останню умову можна записати так: Ця ознака нижче буде використана для класифікації точок розриву. Означення 3. Якщо функція неперервна в кожній точці деякого інтервалу (а, b), то її називають неперервною в інтервалу (а, b). Якщо функція визначена при х = а i Якщо Якщо
Класифікація розривів функції Якщо при деякому х = x1 будь-яка із умов неперервності означення 2 не виконується, то кажуть, що функція в цій точці має розрив, а точку x1 називають точкою розриву функції (дивись Мал. 1.).
 х0 х0  (х) (х)   (х0). В точках х, та х, інша ситуація. При наближенні х до х1 зліва (х0). В точках х, та х, інша ситуація. При наближенні х до х1 зліва  (х) (х)  а, а при х а, а при х  х, справа х, справа  (х) (х) 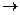 b, тобто b, тобто 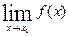 залежить від способу прямування х до х1. В точці х2 умова неперервності функції також не виконується тому, що залежить від способу прямування х до х1. В точці х2 умова неперервності функції також не виконується тому, що 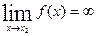 , тобто не існує скінченної границі. , тобто не існує скінченної границі.Графік функції, що зображений на Малюнку 1 має розриви в точках х1 та х2 Розриви функції бувають ліквідовні та неліквідовні: 1) якщо функція
то розрив в точці х1 називають ліквідовним. В цьому випадку функцію можна визначити або змінити її значення в точці х, так, щоб виконувались рівності
2) неліквідовні розриви поділяються на розриви першого та другого роду. а) якщо однобічні границі функції b) якщо хоч би одна з однобічних границь не існує або дорівнює На Малюнку 1 функція має розрив першого роду в точці х1, її стрибок дорівнює b - а, а в точці х2 функція має розрив другого роди.
Властивості неперервних функцій та дії з ними Приведемо без доведень властивості неперервних функцій. Теорема 1. (Вейєрштрасса) Якщо функція у =
для усіх х Теорема 2. Усі основні елементарні функції неперервні в кожній точці своєї області існування. Теорема 3. Алгебраїчна сума, добуток (скінченної кількості доданків та множників) та частка функцій, неперервних при x = х0 (в останньому випадку дільник в цій точці не повинен дорівнювати нулю) є також неперервна функція при х = х0. Теорема 4. Неперервна функція від неперервної функції є також неперервна функція. Теорема 5. Будь-яка елементарна функція неперервна в кожній точці своєї області існування.
Задачі, що приводять до поняття похідної. Означення похідної. Її геометричний та механічний зміст. Дотична до кривої. Вступні відомості Нехай матеріальна точка рухається прямолінійно, а закон руху її задається деякою функцією 1. Поставимо задачу: знайти швидкість точки в момент часу Нехай в деякий момент часу Відношення називається середньою швидкістю руху точки. Означення. Швидкістю Зазначимо, що формула дає змогу знайти швидкість у момент часу
Рис.6.1 2. Задача про дотичну до кривої. З поняттям дотичної до кривої в даній точці ми зустрічалися при вивченні кола за шкільною програмою, за якою давалося означення дотичної до кола як прямої лінії, що має з колом одну спільну точку. Проте це означення є окремим випадком. Його не можна поширити, наприклад, на незамкнуті криві. Тому треба дати загальне означення дотичної, яке б підходило як до замкнутих, так і до незамкнутих кривих. Нехай маємо деяку довільну криву
Рис.6.2 Рис.6.3 Означення. Дотичною до кривої
Рис.6.4
Означення похідної Нехай функція
Якщо границя (4.1) існує і скінченна, вона називається похідною функції
Означення. Похідною функції Операція знаходження похідної називається диференціюванням цієї функції. Користуючись означенням похідної, знайти похідні функцій. Приклад. Функція у = х 2. Знайти похідну в точках х = 3 і х = – 4. l Надамо аргументу х приросту Складемо відношення приросту функції до приросту аргументу Похідна в точці х = 3 Приклад. l Надавши аргументу
Приклад. l Користуючись відомою з тригонометрії формулою
знайдемо приріст функції у точці
Аналогічно можна дістати: Приклад. l Для цієї функції маємо
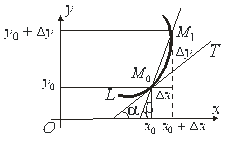
тобто Геометричний зміст похідної Означення. Дотичною до кривої L у точці М називається граничне положення МN січної ММ 1 при прямуванні точки М 1 по кривій L до точки М (рис. 4.1). Нехай крива, задана рівнянням З Таким чином,
Рис. 4.1 Рис. 4.2 Оскільки Механічний зміст похідної Припустимо, що точка М рухається прямолінійно нерівномірно по деякій прямій лінії, яку візьмемо за вісь Ох (рис. 4.3).
Рух точки відбувається за законом х = f (t), де х — шлях; t — час. Знайдемо швидкість точки М у да- Нехай точка М у момент t перебувала на відстані х від початкової точки М 0, а в момент часу Якщо точка М рухається рівномірно, то V cр є величина стала, і її беруть за швидкість точки. Для нерівномірного руху точки очевидно, що для достатньо близьких значень
яка є швидкістю зміни функції х = f (t) у точці. У цьому полягає механічний зміст похідної.
|
|||||||
|
Последнее изменение этой страницы: 2016-04-19; просмотров: 612; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 18.116.90.57 (0.008 с.) |

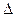 х.
х.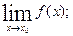 ;
;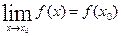 незалежно від способу прямування х до х0,
незалежно від способу прямування х до х0,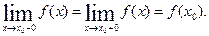
 .
.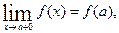 то кажуть, що
то кажуть, що 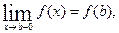 то кажуть, що
то кажуть, що  Поняття неперервності та розриву функції можна наочно показати на графіку функції.
Поняття неперервності та розриву функції можна наочно показати на графіку функції.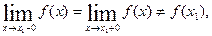

 існують та скінченні, але не рівні між собою, то х1 називають точкою розриву першого роду, а різницю
існують та скінченні, але не рівні між собою, то х1 називають точкою розриву першого роду, а різницю 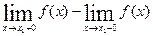 називають стрибком функції;
називають стрибком функції; , то розрив в цій точці називають розривом другого роду.
, то розрив в цій точці називають розривом другого роду.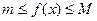
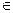 [а, b].
[а, b].
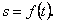 (6.1)
(6.1) .
. (рис.6.1).Через проміжок часу
(рис.6.1).Через проміжок часу  точка займе положення
точка займе положення  і пройде шлях
і пройде шлях  .
. (6.2)
(6.2) точки в момент часу
точки в момент часу  на проміжку часу
на проміжку часу  (6.3)
(6.3)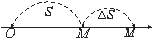
 (рис.6.2, 6.3). Візьмемо на цій кривій точки
(рис.6.2, 6.3). Візьмемо на цій кривій точки  та
та  і через них проведемо пряму
і через них проведемо пряму  , яку називатимемо січною. Якщо точка
, яку називатимемо січною. Якщо точка  , рухаючись вздовж кривої, наближається до точки
, рухаючись вздовж кривої, наближається до точки  прямує до нуля. Якщо при цьому й значення кута
прямує до нуля. Якщо при цьому й значення кута  прямує до нуля, то пряма
прямує до нуля, то пряма  називається граничним положенням січної
називається граничним положенням січної 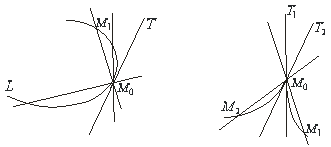
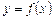 визначена на деякому проміжку (а; b). Візьмемо значення
визначена на деякому проміжку (а; b). Візьмемо значення  і надамо аргументу приросту
і надамо аргументу приросту  . Тоді функція набуде приросту
. Тоді функція набуде приросту  . Розглянемо відношення приросту функції
. Розглянемо відношення приросту функції 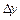 до приросту аргументу
до приросту аргументу  :
: . (4.1)
. (4.1)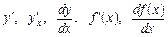 .
. за аргументом х називається границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.
за аргументом х називається границя відношення приросту функції до приросту аргументу, коли приріст аргументу прямує до нуля.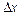 , тоді функція набуде приросту
, тоді функція набуде приросту 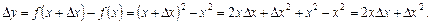
 , відшукаємо границю
, відшукаємо границю 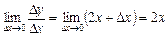 . Таким чином,
. Таким чином, 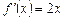 .
.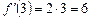 , а похідна при х = – 4 буде
, а похідна при х = – 4 буде  .
. , де
, де  .
. приросту
приросту 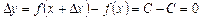 . Тепер знайдемо границю відношення
. Тепер знайдемо границю відношення 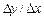 при
при 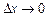 :
: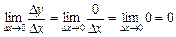 , тобто
, тобто 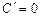
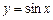 .
.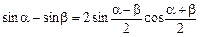 ,
, ,
,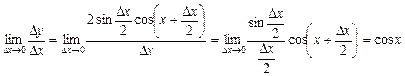 ;
;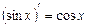 .
. .
. .
.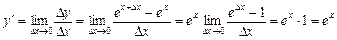 ,
,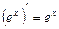 .
.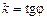 . Надамо в точці х приросту
. Надамо в точці х приросту  випливає, що
випливає, що 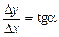 . Коли
. Коли 
 і січна прямує до положення дотичної МN.
і січна прямує до положення дотичної МN.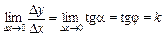 .
.
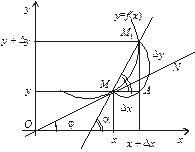
 , то
, то 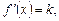 тобто похідна
тобто похідна  чисельно дорівнює кутовому коефіцієнту дотичної, проведеної до графіка функції у точці з абсцисою х. У цьому полягає геометричний зміст похідної.
чисельно дорівнює кутовому коефіцієнту дотичної, проведеної до графіка функції у точці з абсцисою х. У цьому полягає геометричний зміст похідної.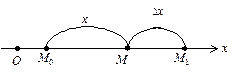 Рис. 4.3
Рис. 4.3
 точка опинилася на відстані
точка опинилася на відстані 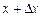 від початкової точки й зайняла положення М 1. Отже, час t набув приросту
від початкової точки й зайняла положення М 1. Отже, час t набув приросту 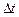 , а шлях х — приросту
, а шлях х — приросту 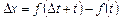 . Середня швидкість руху точки М за час
. Середня швидкість руху точки М за час 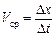 .
.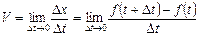 ,
,


