
Заглавная страница Избранные статьи Случайная статья Познавательные статьи Новые добавления Обратная связь FAQ Написать работу КАТЕГОРИИ: ТОП 10 на сайте Приготовление дезинфицирующих растворов различной концентрацииТехника нижней прямой подачи мяча. Франко-прусская война (причины и последствия) Организация работы процедурного кабинета Смысловое и механическое запоминание, их место и роль в усвоении знаний Коммуникативные барьеры и пути их преодоления Обработка изделий медицинского назначения многократного применения Образцы текста публицистического стиля Четыре типа изменения баланса Задачи с ответами для Всероссийской олимпиады по праву 
Мы поможем в написании ваших работ! ЗНАЕТЕ ЛИ ВЫ?
Влияние общества на человека
Приготовление дезинфицирующих растворов различной концентрации Практические работы по географии для 6 класса Организация работы процедурного кабинета Изменения в неживой природе осенью Уборка процедурного кабинета Сольфеджио. Все правила по сольфеджио Балочные системы. Определение реакций опор и моментов защемления |
Неперервність функції двох зміннихСодержание книги
Похожие статьи вашей тематики
Поиск на нашем сайте Означення. Функція
Означення. Функція Означення. Функцію
Означення. Точка 1) функція 2) функція а) б) Означення. Точка
Ця функція має розрив у точці (0, 0), бо в ній для функції Тут ми стикаємося з цікавим явищем: розглядувана функція не є неперервною в точці (0, 0) за двома змінними водночас, але є неперервною за кожною зі змінних х і у окремо. Точки розриву можуть бути не лише ізольованими, як у попередньому прикладі, а можуть заповнювати
розриви заповнюють відповідно гіперболічний параболоїд
●Для будь-якого
Отже,
в точці (0, 0) за множиною, на якій функція визначена. ●Зауважимо, що функція не визначена в точках прямої
в точці (0, 0): 1) є неперервною за прямою 2) неперервною за кривою 3) неперервною. ●1. Наближатимемося до точки (0, 0) по прямій
Якщо 2. Наближатимемося до точки (0, 0) по кривій
Якщо 3. У точці (0, 0) функція
1) 2) ●1. Функція
Для будь-якого
Отже, 2. Функція Тому вона має розриви. Знайдемо границю
Отже, функція
Неперервність складеної (складної) функції двох змінних Означення. Нехай функція
Рис. 12
Теорема 1.6. Нехай на множині D визначено складену функцію Література: В.П.Дубовик, І.І.Юрик „Вища математика”, К.,”АСК”,2001 гл.6, стор. 284 – 294.
Тема 17 Диференційованість функції багатьох змінних. Похідна за напрямом. Градієнт.
Мета заняття Засвоєння понять похідної за напрямом та градієнта; розвивати логічне мислення, виховувати інтерес до математики.
Студенти повинні знати: поняття диференційованості функції багатьох змінних; формули похідної за напрямом та градієнта функції. Студенти повинні вміти: обчислювати похідну за напрямом та градієнт функції.
Основні питання теми 1.Поняття диференційованої функції в точці; 2.Неперервність диференційованої функції; 3.Існування частинних похідних диференційованої функції; 4.Достатня умова диференційованості; 5.Повний диференціал та його застосування до обчислення функцій і похибок. 6.Диференціали вищих порядків; 7.Похідна за напрямом; 8.Градієнт; 9.Приклади
|
||
|
Последнее изменение этой страницы: 2016-08-26; просмотров: 567; Нарушение авторского права страницы; Мы поможем в написании вашей работы! infopedia.su Все материалы представленные на сайте исключительно с целью ознакомления читателями и не преследуют коммерческих целей или нарушение авторских прав. Обратная связь - 216.73.216.214 (0.01 с.) |

 називається неперервною в точці
називається неперервною в точці  , якщо
, якщо .
. , визначену на множині D Ì R 2, називають неперервною за множиною Е Ì D в точці (х 0, у 0)
, визначену на множині D Ì R 2, називають неперервною за множиною Е Ì D в точці (х 0, у 0)  D,якщо
D,якщо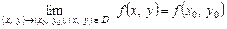 .
.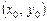 називається точкою розриву функції
називається точкою розриву функції  визначена в точці
визначена в точці  не існує;
не існує; .
. називається точкою усувного розриву функції
називається точкою усувного розриву функції  , якщо
, якщо  існує, але або
існує, але або  не визначена в точці
не визначена в точці 
 Розглянемо функцію двох незалежних змінних
Розглянемо функцію двох незалежних змінних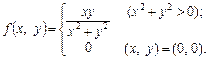
 ,
, 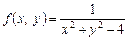 мають розриви: перша — прямі
мають розриви: перша — прямі  друга — окіл
друга — окіл 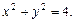 Для функції трьох змінних
Для функції трьох змінних ,
, 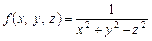
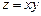 і конус
і конус 
 .
. існує
існує  , таке що для всіх точок
, таке що для всіх точок 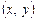 , які задовольняють умову
, які задовольняють умову  і відмінні від початку координат, справджується нерівність
і відмінні від початку координат, справджується нерівність
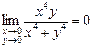 .
.
 . Тому звичайної границі в точці (0, 0) не існує. Але границя за множиною точок
. Тому звичайної границі в точці (0, 0) не існує. Але границя за множиною точок  , на якій функція визначена, існує і дорівнює нулю, оскільки
, на якій функція визначена, існує і дорівнює нулю, оскільки .
.
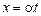 ,
,  ,
,  ;
; ;
; .
.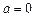 , то дана функція буде неперервною за даною прямою.
, то дана функція буде неперервною за даною прямою. .
. , то розглядувана функція буде неперервною за даною прямою.
, то розглядувана функція буде неперервною за даною прямою. має розрив, оскільки в ній границя не існує. Це випливає з 1 і 2.
має розрив, оскільки в ній границя не існує. Це випливає з 1 і 2. ;
; .
. в точці (0, 0) не існує, тому вона має в цій точці розрив. Знайдемо границю
в точці (0, 0) не існує, тому вона має в цій точці розрив. Знайдемо границю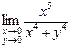 .
. існує
існує 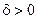 , таке що для всіх точок
, таке що для всіх точок 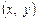 , які задовольняють умову
, які задовольняють умову  і відмінні від початку координат, виконується нерівність
і відмінні від початку координат, виконується нерівність .
. і функція має в точці (0, 0) усувний розрив, якщо
і функція має в точці (0, 0) усувний розрив, якщо  у цій точці.
у цій точці. , тобто
, тобто  ,
,  ,
,  .
.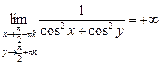 .
. має в точці
має в точці 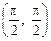 неусувний розрив.
неусувний розрив.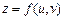 визначена на множині Е, а змінні
визначена на множині Е, а змінні  і
і  , у свою чергу, залежать від змінних х і у:
, у свою чергу, залежать від змінних х і у: 
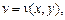 причому обидві функції
причому обидві функції  та
та  визначені на множині D. Якщо для будь-якого
визначені на множині D. Якщо для будь-якого  існує значення
існує значення  (рис. 12), то говорять, що на множині визначено складену (складну) функцію
(рис. 12), то говорять, що на множині визначено складену (складну) функцію 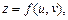 де
де 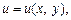

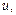

 де
де 
 . Це складена функція, яка визначена на координатній площині. Її можна записати у вигляді
. Це складена функція, яка визначена на координатній площині. Її можна записати у вигляді .
. , де
, де  ,
,  і нехай функції
і нехай функції  ,
,  неперервні в точці
неперервні в точці  , а функція
, а функція 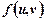 неперервна в точці
неперервна в точці  , де
, де  ,
,  . Тоді складена функція
. Тоді складена функція  неперервна в точці
неперервна в точці 



